1. Аксиомы статики твердого тела.
Аксиома 1
(о равновесии двух сил). Две силы,
приложенные к абсолютно твердому телу,
уравновешиваются тогда и только тогда,
когда они равны по величине,
противонаправлены и имеют общую линию
действия (рис. 1.4).
Аксиома 2 (о присоединении и исключении уравновешенных сил). Действие данной системы сил на твердое тело не изменяется, если к ней присоединить или исключить из нее уравновешенную систему.
Из аксиом 1 и 2 логически получаем следствие: не изменяя действия силы на твердое тело, можно переносить точку приложения силы вдоль линии действия.
Система сил наз. уравновешенной, если равнодействующая этой системы равна нулю ( FΣ=0 )
Если равнодействующая системы сил, действующих на материальную точку, не равна 0, то эту систему можно уравновесить, приложив к точке уравновешивающую силу Fу, равную Fу = - FΣ
При нахождении равнодействующей двух сил используется также правило параллелограмма: равнодействующая сила FΣ равна диагонали параллелограмма, сторонами которого являются две складываемые силы F1 и F2.
Точка приложения силы к абсолютному твердому телу может быть перенесена вдоль линии действия этой силы (перенос точки приложения силы в абсолютно твердом теле)
Момент силы относительно точки. Разложение момента силы по декартовой системе координат.
Момент силы относительно произвольной точки. Пусть частица A движется относительно точки О под действием произвольной силы F (см. рис. 9.3).
Моментом силы M относительно произвольной точки О называется векторное произведение радиус-вектора частицы r, проведенного из точки O в точку приложения силы, на вектор силы F:
M = [r, F].
3. Момент силы относительно оси.
Момент силы относительно оси есть проекция момента силы относительно точки этой оси.
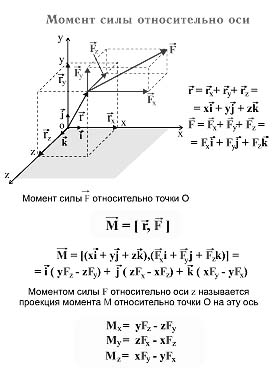
4. Теорема 1:
Моменты силы относительно оси независят от выбора полюса на этой оси.
Вычисление моментов силы относительно оси по этим формулам явл. аналитическим способом.
Теорема 2:
Момент силы оси равен моменту проекции силы на плоскость перпенд. этой оси.
Графоаналитический способ:
Спроецировать силу на плоскость параллельную оси.
Найти плечо проекции
Умножить проекцию на плечо
Взять знак +, если выражение силы предусматривается против часовой стрелки, когда ось в глаз.
Характеристики силы. Сила, действующая на твердое тело. Задание силы.
Сила определяется своей величиной, направлением, точкой приложения. Величина силы практически измеряется в весовых единицах (граммах, килограммах, тоннах), направление совпадает с направлением того движения, которое данная сила сообщила бы телу, находившемуся до приложения силы в состоянии покоя. Сила графически изображается вектором – отрезком, начало которого находится в точке приложения силы; указываемое стрелкой направление совпадает с направлением силы, и длина представляет в некотором масштабе величину силы (АВ на рис.). Точка приложения силы, действующей на твердое тело, может быть без изменения действия силы взята где угодно на прямой, совпадающей с направлением силы.
К системе сил, действующих на твёрдое тело, можно всегда добавить две силы, равные по величине, лежащие на одной прямой и направленные в противоположные стороны.
