
- •Проекции центральные и параллельные
- •3)Метод Гаспара Монжа
- •6) Проекции отрезка прямой линии
- •8) Точка на прямой
- •9) Следы прямой
- •10) Построение на чертеже натуральной величины
- •1Определены из прямоугольного треугольника, построенного на проекции а'в'
- •12) О проекциях плоских углов
- •1. Если плоскость, которой расположен некоторый угол, перпендикулярна
- •2. Если плоскость прямого угла не перпендикулярна к плоскости проекций
- •3. Если проекция плоского угла представляет собой прямой угол, то
- •4. Если проекция некоторого угла, у которого одна сторона параллельна
- •2) Интересующихся доказательством обратных теорем отсылаем к
- •5. Ecли плоскость тупого или острого угла не перпендикулярна к
- •6. Если обе стороны любого угла, параллельны плоскости проекций, то его
- •0; С°в° || св. Пл. , проведенная через точку с перпендикулярно к св,
- •13) Различные способы задания плоскости на чертеже
- •14) Следы плоскости
- •15)16)Прямая и точка в плоскости. Прямые особого положения
- •1) Прямая принадлежит плоскости, если она проходит через две точки,
- •2) Прямая принадлежит плоскости, если она проходит через точку,
- •2) Для линии ската плоскости распространено название "линия
- •108, Справа, на котором изображена пл. И прямая mb, устанавливаем, что эта
- •17) Построение линии пересечения двух плоскостей
- •1, В своем пересечении определяют первую точку, к1, линии пересечения
- •1'2', И 3'4', следует для проекций 5'6' и 7'8' взять по одной
- •167 Показывает, что и пересекаются между собой, хотя их горизонтали
- •22) Построение взаимно перпендикулярных прямой и плоскости
- •1) Через точку а провести плоскость (назовем ее ), перпендикулярную к
- •2) Определить точку к пересечения прямой вс с ил. ;
- •1,2 Дополнительной плоскости и образования, таким образом, системы 3, 1,
- •90°. Аналогично, если пл. Составляет с пл. 2 угол ?, а прямая am,
- •23) Построение взаимно перпендикулярных плоскостей
- •194 Горизонтально-проецирующая плоскость проходит через точку к
- •31. Построение проекций угла между прямой и плоскостью и между двумя
194 Горизонтально-проецирующая плоскость проходит через точку к
перпендикулярно к плоскости, заданной треугольником ABC. Здесь
дополнительным условием явля-
77
лась перпендикулярность искомой плоскости сразу к двум плоскостям: к
пл. ABC и к пл. ,. Поэтому и ответом служит горизонтально-проецирующая
плоскость. А так как она проведена перпендикулярно к горизонтали AD, т. е. к
прямой, принадлежащей пл. ABC, то пл. перпендикулярна к пл. ABC.
Может ли перпендикулярность одноименных следов плоскостей служить
признаком перпендикулярности самих плоскостей?
К очевидным случаям, когда это так, относится взаимная
перпендикулярность двух горизонтально-проецирующих плоскостей, у которых
горизонтальные следы взаимно перпендикулярны. Также это имеет место при
взаимной перпендикулярности фронтальных следов фронтально-проецирующих
плоскостей; эти плоскости взаимно перпендикулярны.
Рассмотрим (рис. 195) горизонтально-проецирующую плоскость ,
перпендикулярную к плоскости общего положения а.
Если пл. перпендикулярна к пл. 1 и к пл. , то % h'o как к линии
пересечения пл. и пл. ,. Отсюда h'o% и, следовательно, h'o % ', как
к одной из прямых в пл. .
Итак, перпендикулярность горизонтальных следов плоскости общего
положения и горизонтально-проецирующей соответствует взаимной
перпендикулярности этих плоскостей.
Очевидно, перпендикулярность фронтальных следов фронтально-проецирующей
плоскости и плоскости общего положения также соответствует взаимной
перпендикулярности этих плоскостей.

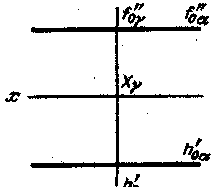
Рис. 196
Но если одноименные следы двух плоскостей общего положения взаимно
перпендикулярны, то самые плоскости не перпендикулярны между собой, так как
здесь не соблюдается ни одно из условий, изложенных в начале этого
параграфа.
В заключение рассмотрим рис. 196. Здесь имеет место случай взаимной
перпендикулярности одноименных следов в обеих их парах и перпендикулярности
самих плоскостей: обе плоскости особого (частного) положения -- профильная
и профильно-проецирующая
31. Построение проекций угла между прямой и плоскостью и между двумя
ПЛОСКОСТЯМИ
Если прямая не перпендикулярна к плоскости, то углом между прямой и
плоскостью называют угол между этой прямой и ее проекцией на данной
плоскости.
Об углах между прямой и плоскостями проекций см, 13.
На рис. 197 изображена прямая АВ, пересекающая пл, 0 в точке D; угол
образован отрезком BD данной прямой и проекцией B°D этого отрезка на пл. 0.
78
Построение проекций угла между прямой АВ и некоторой пл. выполнено на
рис. 198. Пл. задана ее горизонталью (проекции Р"Н" и Р'Н') и фронталью
(проекции P"F" и PF).
Построение выполнено в следующем порядке:
а) найдена точка D пересечения прямой АВ с пл. о, для чего через АВ
проведена горизонтально-проецирующая плоскость ;
б) из точки А проведен перпендикуляр к пл. а;
в) найдена точка пересечения этого перпендикуляра с пл.' ос, для чего
проведена горизонтально-проецирующая плоскость ;
г) через точки D" и Е", D' и проведены прямые, чем определяются
проекции прямой АВ на пл. .
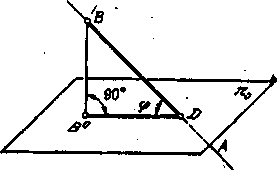
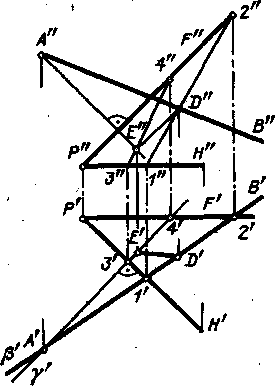
Рис. 197 Рис. 198
Угол A"D"E" представляет собой фронтальную проекцию угла между АВ и пл.
, а угол A'D Е' -- горизонтальную проекцию этого угла.
Построение проекции угла между прямой и плоскостью значительно
упрощается, если плоскость не является плоскостью общего положения, так как
в подобных случаях точка пересечения заданной прямой с плоскостью
определяется без дополнительных построений.
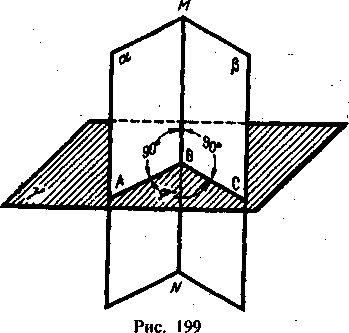
Две пересекающиеся между собой плоскости образуют четыре двугранных
угла. Ограничиваясь рассмотрением угла между и , показанного на рис. 199,
построим его линейный угол, для чего пересечем ребро двугранного угла
плоскостью , перпендикулярной к .
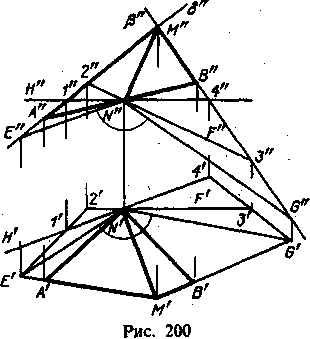
Построение проекций линейного угла выполнено на рис. 200. Пл. ос задана
треугольником , пл. -- треугольником .
а) Построена пл. % , проходящая через точку N (пл. задана ее
фронталью NF и горизонталью ).
79
б) Построена линия пересечения плоскостей и (прямая E); так как
пл. проведена через точку N пл. о, то надо найти только точку Е, для чего
взята вспо-
могательная плоскость .
в) Найдена линия пересечения плоскостей и (прямая NG); здесь также
надо было найти только точку G (вспомогательная пл. ).
Точка N является вершиной искомого линейного угла, угол E'N'G'
представляет собой горизонтальную проекцию этого угла, угол E'N"G" -- его
фронтальную проекцию.
На рис. 195 построены проекции линейного угла, измеряющего двугранный
угол, образуемый пл. с плоскостью проекций к,. Так как для получения
линейного угла надо провести плоскость, перпендикулярную к ребру двугранного
угла, то для получения утла наклона пл. к пл. , проведена пл. ,
перпендикулярная к следу h'o. Аналогично, для получения угла между пл. и
пл. 2 надо было бы провести плоскость перпендикулярно к. следу f"o.
На рис. 195 фронтальной проекцией искомого угла является угол ""', а
горизонтальная проекция угла совпадает со следом ". Величина угла может
быть определена построением прямоугольного,треугольника по катетам "' и
''.
