Тема 1.5. Формулы Крамера.

Если число строк совпадает с числом столбцов, т.е. m=n, то матрица А- квадратная и ее определитель - главный определитель системы. Когда главный определитель не равен 0 решение системы единственно и находится по формулам Крамера.

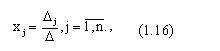
Теорема Крамера. Система n линейных уравнений с n неизвестными имеет единственное решение, если определитель системы не равен 0, и это решение находится по формуле Крамера:

где определители D называются определителями неизвестных хj и получаются из главного определителя путем замены j-го столбца столбцом свободных членов.

Уровень 2. Для доказательства рассмотрим систему (1.7). Пусть определитель не равен 0. Умножим первое уравнение на алгебраическое дополнение А11, второе уравнение на А21, третье уравнение на А31. Сложим все три уравнения и сгруппируем коэффициенты при одинаковых х. Получим

(А11а11 + А21а21 + А31а31)х1 + (А11а12 + А21а22 + А31а32)х2 + (А11а13 + А21а23+ А31а33)х3 = =А11b1 + A21b2 +A31b3.

25.

ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.

Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы.

Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образует фундаментальную систему решений однородной системы.

примеры

Однородная система линейных алгебраических уравнений

с помощью элементарных преобразований может быть приведена к каноническому виду:

Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3.

три линейно независимые решения системы

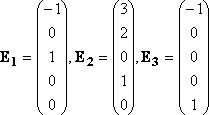
образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений.