
Транспонирование матриц
Определение. Матрицу АТ называют транспонированной матрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы АТ.(т.е. строки матрицы А заменены на столбцы и наоборот)
А
=
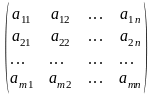 ; АТ=
; АТ= ;
;
Пример: Даны матрицы
А =
 ,
В =
,
В =
 ,
С =
,
С =
 и число
= 2. Найти АТВ+С.
и число
= 2. Найти АТВ+С.
AT
=
 ; ATB
=
=
; ATB
=
=
 =
=
 ;
;
C
=
 ;
АТВ+С
=
+
=
;
АТВ+С
=
+
=
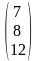 .
.
Пример: Даны матрицы
А =
 и В =
и В =
 .
Найти произведение матриц АВ и ВА.
.
Найти произведение матриц АВ и ВА.
АВ
=
=
 .
.
ВА = = (21 + 44 + 13) = (2 + 16 + 3) = (21).
Пример: Найти
произведение матриц А= ,
В =
,
В =

АВ
=
=
 =
=
 .
.
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование
Обратная матрица
Определение:
Матрица
 называется обратной по отношению к
квадратной матрице
называется обратной по отношению к
квадратной матрице
 ,
если
,
если
 .
.
Обратная матрица существует только для квадратной матрицы, определитель которой не равен нулю. Такая матрица называется невырожденной.
Рассмотрим общий подход к нахождению обратной матрицы.
Рассмотрим на примере, как найти обратную матрицу .
Пусть

1)Найти определитель матрицы
 .
.
Так как
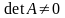 ,
то обратная матрица
существует.
,
то обратная матрица
существует.
2) Сформировать матрицу из алгебраических дополнений каждого элемента матрицы.

если
 - четное число,
- четное число,
если - нечетное число.

3) Транспонируем матрицу из алгебраических дополнений.
 .
.
4) Обратная матрица определяется формулой
 ,
,
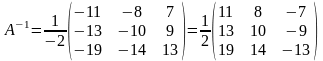 .
.
Укажем следующие свойства обратных матриц:
(A-1)-1 = A;
(AB)-1 = B-1A-1
(AT)-1 = (A-1)T.
2.
Квадратная матрица
В случае, когда число строк прямоугольной матрицы равно числу ее столбцов, матрица называется квадратной матрицей:

n -порядок квадратной матрицы.
Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю

Диагональная матрица является симметричной:
DT = D.
Ранг диагональной матрицы равен количеству ненулевых элементов, находящихся на главной диагонали.
Определитель диагональной матрицы равен произведению диагональных элементов:
![]()
Примеры
 Нулевая
матрица
Нулевая
матрица
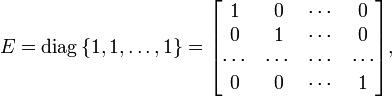 единичная
матрица
единичная
матрица
Скалярная матрица — диагональная матрица, элементы главной диагонали которой равны. Частным случаем скалярной матрицы является единичная матрица

Свойства
Скалярная матрица — это произведение скаляра и единичной матрицы.
![]()
Множество скалярных матриц — это ровно все те матрицы, которые коммутируют со всеми квадратными матрицами того же размера, то есть для любой матрицы A и скалярной матрицы S того же размера: AS = SA.
единичная матрица - квадратная матрица, все диагональные элементы которой единицы, а остальные - нули:
Единичная
матрица размера
![]() обычно обозначается En и имеет вид:
обычно обозначается En и имеет вид:

Свойства
Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:
AE = EA = A
Квадратная матрица в нулевой степени дает единичную матрицу того же размера:
A0 = E
При умножении матрицы на обратную ей тоже получается единичная матрица:
![]()
Единичная матрица получается при умножении ортогональной матрицы на ей транспонированную:
AAT = E
Определитель единичной матрицы равен единице:
![]()
Примеры
Единичные матрицы первых порядков имеют вид

3.
Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы.
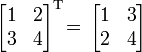 и
и

Свойства транспонированных матриц
Дважды транспонированная матрица А равна исходной матрице А.
![]()
Транспонированная сумма матриц равна сумме транспонированных матриц.
![]()
Транспонированное произведение матриц равно произведению транспонированных матриц
![]()
При транспонировании можно выносить скаляр.
![]()
Определитель транспонированной матрицы равен определителю исходной матрицы
![]()
4.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Определение
Элементарными преобразованиями строк называют:
перестановка местами любых двух строк матрицы;
умножение любой строки матрицы на константу
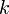 ,
,
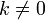
прибавление к любой строке матрицы другой строки, умноженной на константу ,
Обозначение
![]() указывает на то, что матрица
указывает на то, что матрица
![]() может быть получена из
может быть получена из
![]() путём элементарных преобразований
(или наоборот)
путём элементарных преобразований
(или наоборот)
Свойства
Инвариантность ранга при элементарных преобразованиях
Теорема (об инвариантности ранга при элементарных преобразованиях)
Если
,
то
![]()
Эквивалентность СЛАУ при элементарных преобразованиях
Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:
перестановку уравнений;
умножение уравнения на ненулевую константу;
сложение одного уравнения с другим, умноженным на некоторую константу.
Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
Теорема (об эквивалентности систем уравнений при элементарных преобразованиях).
Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей
Нахождение обратных матриц
Теорема (о нахождении обратной матрицы).
Пусть
определитель матрицы
![]() не равен нулю, пусть матрица
определяется выражением
не равен нулю, пусть матрица
определяется выражением
![]() . Тогда при элементарном преобразовании
строк матрицы
к единичной матрице
. Тогда при элементарном преобразовании
строк матрицы
к единичной матрице
![]() в составе
одновременно происходит преобразование
к
в составе
одновременно происходит преобразование
к
![]()
Приведение матриц к ступенчатому виду
Введём понятие ступенчатых матриц:
Матрица имеет ступенчатый вид, если:
Все нулевые строки матрицы стоят последними;
Для
любой ненулевой строки матрицы
(пусть для определённости её номер равен
) справедливо следующее: если
![]() — первый ненулевой элемент строки
, то
— первый ненулевой элемент строки
, то
![]() .
.
Тогда справедливо следующее утверждение:
Теорема (о приведении матриц к ступенчатому виду).
Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.
Эквивалентные матрицы
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.
5.
Блочная (клеточная) матрица — вид квадратной матрицы, каждый элемент которой является квадратной подматрицей меньшей, кратной размерности.
Пример записи
Матрица размерностью 4×4
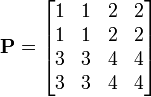
является блочной, состоящей из четырех подматриц-блоков размерностью 2×2
Если каждый блок будет определен как
![]()
то, блочная матрица может быть записана в следующем виде
![]()
Операции с блочными матрицами
При сложении блочных матриц нужно, чтобы подматрицы были одного размера.
При умножении блочной матрицы на число a каждая подматрица умножается на a.
При перемножении блочных матриц необходимо согласовать размеры подматриц.
При транспонировании блоки на главной диагонали транспонируются и остаются на месте, остальные блоки меняются местами и транспонируются.
6.
Определители второго и третьего порядков
Метод Гаусса, рассмотренный выше, весьма прост, состоит из однотипных вычислений и не требует больших усилий при алгоритмической реализации. Однако его существенным недостатком является то, что он не дает возможность сформулировать условия совместности или определенности системы по информации о коэффициентах и свободных членах этой системы. С другой стороны, даже при условии определенности системы этот метод не позволяет построить формулы, выражающие решение системы через ее коэффициенты и свободные члены. Все это, однако, оказывается необходимым при решении различных теоретических вопросов, в частности в геометрических исследованиях. Поэтому теорию систем линейных алгебраических уравнений приходится развивать иными, более глубокими методами.
Сначала рассмотрим частный случай определенных систем, имеющих равное число уравнений и неизвестных.
Пусть дана система двух линейных уравнений с двумя неизвестными
![]() (1)
(1)
коэффициенты которого составляют квадратную матрицу второго порядка
![]() (2)
(2)
Применяя к системе (1) метод уравнивания коэффициентов (первое уравнение умножаем на a22, а второе – на a12 и получаем выражение для x1, аналогично – для x2) получим:
![]()
предположим, что a11a22 – a12a21¹0. Тогда
![]() (3)
(3)
Общий знаменатель значений неизвестных (3) легко выражается через элементы матрицы (2): он равен произведению элементов главной диагонали минус произведение элементов второй диагонали. Это число называется определителем или детерминантом матрицы (2), причем, как говорят, определителем второго порядка, т. к. матрица (2) есть матрица второго порядка. Для обозначения определителя матрицы (2) употребляется следующий символ:
![]() (4)
(4)
Произведения а11 а22 - а12 а21 называются членами определителя второго порядка.
Итак, матрица есть таблица чисел, а определитель – число, соответствующее матрице.
Примеры:
1)
![]() 2)
2)
![]()
Числитель выражений (3) имеет такой же вид, как и знаменатель, т. е. это тоже знаменатель второго порядка. Числитель выражения для x1 есть определитель матрицы, получающейся из матрицы (2) заменой ее первого столбца столбцом из свободных членов системы (1), а числитель выражения для x2 есть определитель матрицы, получающейся из матрицы (2) такой же заменой ее второго столбца. Таким образом, формулы (3) в новых обозначениях записываются в следующем виде:
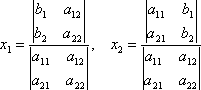 (5)
(5)
Это и есть правило Крамера решения системы двух линейных уравнений с двумя неизвестными:
Если определитель (4) из коэффициентов системы уравнений (1) отличен от нуля, то получаем решение системы (1), беря в качестве значений для неизвестных дроби, общим знаменателем которых служит определитель (4) матрицы коэффициентов системы (1), а числителем для неизвестного хi (i=1,2) является определитель, получающийся заменой в определителе (4) i-го столбца (т. е. столбца коэффициентов при неизвестном) столбцом из свободных членов системы (1).
Пример:
![]()
Определитель из коэффициентов есть
![]()
Он отличен от нуля, и поэтому к системе применимо правило Крамера. Числителями для неизвестных будут определители
![]()
Таким образом, решением системы служит следующая пара чисел:
![]()
Введение определителей второго порядка не вносит существенных упрощений в решение систем двух линейных уравнений с двумя неизвестными, и без того не представляющее никаких трудностей. Однако, уже для случая трех уравнений с тремя неизвестными аналогичные методы становятся практически полезными.
Пусть дана система
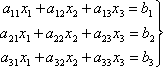 (6)
(6)
с квадратной матрицей из коэффициентов
 (7)
(7)
Если мы умножим обе части первого из уравнений (6) на число а22а33 - а23а32, обе части второго – на а13а32 - а12а33, обе части третьего – на а12а23 - а13а22, а затем сложим все три уравнения, то, как легко проверить, коэффициенты при х2 и х3 окажутся равными нулю, т. е. эти неизвестные одновременно исключаются, и мы получим равенство:
(a11a22a33+ a12a23a31+ a13a21a32- a13a22a31- a12a21a33- a11a23a32)х1=
= b1a22a33+ a12a23b3+ a13b2a32- a13a22b3- a12b2a33- b1a23a32 (8)
Коэффициенты при х1 в этом равенстве называются определителем третьего порядка, соответствующим матрице (7). Для его записи употребляется такая же символика, как и в случае определителя второго порядка:
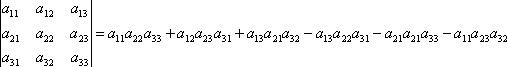 (9)
(9)
Хотя выражение определителя третьего порядка выглядит весьма громоздким, закон его составления из элементов матрицы (7) оказывается довольно простым. В самом деле, один из трех членов определителя, входящих со знаком «плюс» есть произведение элементов главной диагонали, каждый из двух других – произведением элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла матрицы. Члены, входящие в (9) со знаком «минус» строятся также, но относительно второй диагонали. На рис. 1 слева указано правило вычисления положительных членов определителя третьего порядка, а справа – правило вычисления отрицательных членов. Это правило называется правилом Саррюса.
Шесть основных свойств определителя 3-го порядка.
Определители третьего порядка (как и определители 2-го порядка) обладают следующими шестью свойствами, следующими из формулы (9) (для определителей второго порядка – из формулы (4)).
1. определитель не изменится, если строки его матрицы сделать столбцами, а столбцы строками;
2. при перестановке двух строк определителя он меняет знак;
3. если в определителе имеются две одинаковые строки, то определитель равен нулю;
4. общий множитель определителя строки можно вынести за знак определителя;
5. если элементы одной строки определителя пропорциональны элементам другой, то определитель равен нулю;
6. если к одной строке определителя прибавить другую, умноженную на любое число, то определитель не изменится.
Примеры:
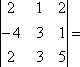 2×3×5+1×1×2+2×(-4)×3-2×3×2-1×(-4)×5-2×1×3=30
+ 2 – 24 – 12 +20 – 6 =10
2×3×5+1×1×2+2×(-4)×3-2×3×2-1×(-4)×5-2×1×3=30
+ 2 – 24 – 12 +20 – 6 =10
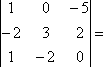 1×3×0+0×2×1+(-5)×(-2)×(-2)-(-5)×3×1-0×(-2)×0-1×2×(-3)=
1×3×0+0×2×1+(-5)×(-2)×(-2)-(-5)×3×1-0×(-2)×0-1×2×(-3)=
= -20 + 15 +4 = - 1
Правая часть равенства (8) также будет определителем третьего порядка, а именно определителем матрицы, получающейся из матрицы (7) заменой ее первого столбца столбцом из свободных членов системы (6). Обозначим определитель (9) символом D, а определитель матрицы, получающейся заменой j-го столбца столбцом из свободных членов системы (6) символом D1. Тогда равенство (8) приобретает вид D×x1=D1, откуда при D¹0 следует
![]() (10)
(10)
Таким же путем, умножая уравнения (6) соответственно на числа а23а31 – а21а33, а11а33 – а13а31, а13а21 – а11а23, получим для х2 следующее выражение (снова при d¹0):
![]() (11)
(11)
Наконец, умножая уравнения (6) соответственно на а21а32 – а22а31, а12а31 – а11а32, а11а22 – а12а21, придем к выражению для х3:
![]() (12)
(12)
Таким образом, если определитель из коэффициентов системы трех линейных уравнений с тремя неизвестными отличен от нуля, то решение этой системы может быть найдено по правилу Крамера, формулируемому также, как и в случае системы двух уравнений.
Пример: Решить систему:

Определитель из коэффициентов системы отличен от нуля:
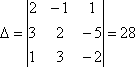
поэтому к системе применимо правило Крамера. Числителями для неизвестных будут определители
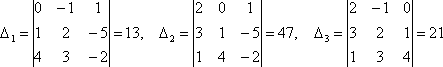
т. е. решением системы являются следующие значения хi:
![]()
7.
Минор
![]() матрицы A ― определитель квадратной
матрицы порядка k (который называется
также порядком этого минора), элементы
которой стоят в матрице A на пересечении
строк с номерами
матрицы A ― определитель квадратной
матрицы порядка k (который называется
также порядком этого минора), элементы
которой стоят в матрице A на пересечении
строк с номерами
![]() и столбцов с номерами
и столбцов с номерами![]() .
.
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
Пример
Например, есть матрица:
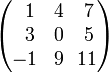
Предположим, надо найти дополнительный минор . Этот минор — определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:
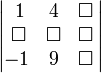

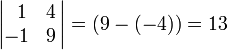
Получаем
![]()
8.
Алгебраические дополнения:
Алгебраическим дополнением элемента аij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается Аij.
Аij = (-1)i+j × Мij.
Тогда можно переформулировать изложенное выше свойство. Определитель матрицы равен сумме произведение элементов некторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения. Пример:
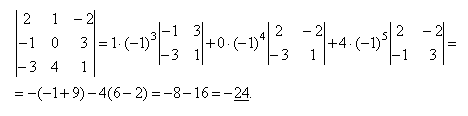
9.
Определение через разложение по первой строке
Схема расчета определителя матрицы .
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
![]()
Для матрицы
![]() детерминант определяется как
детерминант определяется как
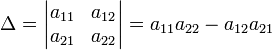
Для матрицы определитель задаётся рекурсивно:
 , где
, где
![]() — дополнительный минор к элементу a1j.
Эта формула называется разложением по
строке.
— дополнительный минор к элементу a1j.
Эта формула называется разложением по
строке.
В частности, формула
вычисления определителя матрицы
![]() такова:
такова:
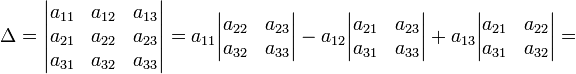 =
a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 −
a13a22a31
=
a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 −
a13a22a31
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
![]()
10.
Основные свойства определителей
Прежде всего отметим, что det[A] = det[A]t, т. е. определитель матрицы не изменяет своего значения при взаимной замене ее строк и столбцов. Поэтому все свойства определителя, сформулированные для столбцов, справедливы и для строк, и обратно.
Ниже приводятся основные свойства определителей, которые легко доказываются на основе общего выражения (1).
1. При перестановке двух столбцов определитель меняет знак на противоположный (свойство антисимметрии).
2. Определитель равен нулю, если все элементы какого-нибудь столбца равны нулю или если один из столбцов является линейной комбинацией любых его других столбцов (в частности, определитель, у которого хотя бы два столбца одинаковы, равен нулю).
3. Умножение всех элементов какого-нибудь столбца на скаляр k равнозначно умножению определителя на k (общий множитель элементов строки или столбца можно вынести за знак определителя).
4. Умножение матрицы n-го порядка на скаляр k соответствует умножению ее определителя на kn, т.е.
det(k[A]) = kndet[A].
5. Значение определителя не изменится, если к какому-нибудь столбцу прибавить другой столбец, умноженный на скаляр k.
6. Если два определителя одинаковых порядков различаются между собой только элементами j-го столбца, то их сумма равна определителю, элементы j-го столбца которого равны суммам соответствующих элементов j-х столбцов исходных определителей, а остальные элементы те же, что у исходных (свойство линейности).
11.
Невырожденные матрицы
Пусть А - квадратная матрица n - ого порядка.

Квадратная матрица А называется невырожденной, если определитель матрицы (Δ = det A) не равен нулю (Δ = det A ≠ 0). В противном случае (Δ = 0) матрица А называется вырожденной.
Матрицей, союзной к матрице А, называется матрица

, где Аij - алгебраическое дополнение элемента аij данной матрицы (оно определяется так же, как и алгебраическое дополнение элемента определителя матрицы).
Матрица А-1 называется обратной матрице А, если выполняется условие:
А × А-1 = А-1 × А = Е
, где Е - единичная матрица того же порядка, что и матрица А. Матрица А-1 имеет те же размеры, что и матрица А.
12.
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
![]()
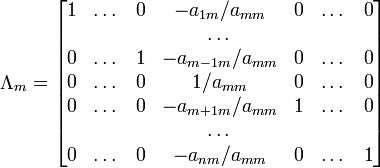
Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n3).
С помощью матрицы алгебраических дополнений
![]() ,
где CT — транспонированная матрица
алгебраических дополнений;
,
где CT — транспонированная матрица
алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
13.
Обратная матрица вычисляется по формуле
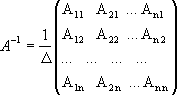
14.
Свойства обратной матрицы
![]() ,
где
,
где
![]() обозначает определитель.
обозначает определитель.
![]() для любых двух обратимых матриц A и B.
для любых двух обратимых матриц A и B.
![]() где * T обозначает транспонированную
матрицу.
где * T обозначает транспонированную
матрицу.
![]() для любого коэффициента
.
для любого коэффициента
.
Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A − 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
15.
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Пусть
![]() — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы A является:
ноль, если A — нулевая матрица;
число
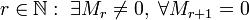 , где Mr — минор матрицы A порядка r, а Mr
+ 1 — окаймляющий к нему минор порядка
(r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr
+ 1 — окаймляющий к нему минор порядка
(r + 1), если они существуют.
Теорема (о корректности
определения рангов). Пусть все миноры
матрицы
порядка k равны нулю (Mk = 0). Тогда![]() , если они существую
, если они существую
16.
Строчнопсевдотреугольная – если в каждой нулевой строке найдется хотябы один нулевой элемент, в столбце которого все нижележащие елементы (если они есть) = 0
Строчнопсевдодиагональная – если в каждой нулевой строке найдется хотябы один нулевой елемент, в столбце которого строго все елементы лежащие выше (если они есть) = 0
17.
Линейное пространство. Основные понятия
Пусть
![]() множество элементов произвольной
природы, для которых определены операции
сложения и умножения на действительное
число:
множество элементов произвольной
природы, для которых определены операции
сложения и умножения на действительное
число:
паре элементов
множества
![]() ,
,
![]() отвечает элемент
отвечает элемент
![]() , называемый суммой
, называемый суммой
![]() и
и
![]() ;
;
паре
,
![]() отвечает элемент
отвечает элемент![]() , называемый произведением числа
, называемый произведением числа
![]() и элемента
.
и элемента
.
Будем называть
множество
линейным пространством, если для всех
его элементов определены операции
сложения и умножения на действительное
число и для любых элементов
![]() и произвольных чисел
и произвольных чисел
![]() справедливо:
справедливо:
![]() ,
сложение коммутативно;
,
сложение коммутативно;
![]() ,
сложение ассоциативно;
,
сложение ассоциативно;
существует единственный
нулевой элемент
![]() такой, что
такой, что
![]() ,
,
![]() ;
;
для каждого элемента
существует единственный противоположный
элемент
![]() такой, что
такой, что
![]() ,
,
![]() ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;
![]() ;
,
;
;
,
;
![]() ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;
![]() ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Равенства 1--8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы – векторам
18.
РАЗМЕРНОСТЬ ЛИЕЙНОГО ПРОСТРАНСТВА
Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима.
Обозначается dimL = k. Пространство L называется k- мерным. Иногда обозначается Lk.
Векторы i и j — линейно независимая система векторов линейного пространства геометрических радиусов-векторов плоскости R2 .
Рассмотрим произвольную систему из трёх векторов x, y, z .

На рисунке показано, что вектор z линейно выражается через векторы x и y: z = α1·x + α2·y.
Итак, в пространстве R2 существует система из двух линейно независимых векторов ( i , j), а любые три вектора образуют линейно зависимую систему. То есть размерность пространства R2 равна 2, dim R2 = 2.
19.
Изоморфи́зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Объекты, между которыми
существует изоморфизм, являются в
определённом смысле «одинаково
устроенными», они называются изоморфными.
Классическим примером изоморфных систем
могут служить множество
![]() всех вещественных чисел с определённой
на нём операцией сложения и множество
всех вещественных чисел с определённой
на нём операцией сложения и множество
![]() положительных вещественных чисел с
заданной на нём операцией умножения.
Отображение
положительных вещественных чисел с
заданной на нём операцией умножения.
Отображение
![]() в этом случае является изоморфизмом.
в этом случае является изоморфизмом.
20.
Определение: W называется подпространством пространства V, если оно само является векторным пространством над полем P.
Теорема 1: Критерий
подпространства. Непустое множество
![]() является подпространством пространства
V тогда и только тогда, когда W замкнуто
относительно сложения векторов и
умножения их на скаляры. Иными словами,
выполняются следующие два условия:
является подпространством пространства
V тогда и только тогда, когда W замкнуто
относительно сложения векторов и
умножения их на скаляры. Иными словами,
выполняются следующие два условия:
![]()
![]()
Теорема 2: Пересечение любого семейства подпространств данного пространства V вновь является подпространством постранства V.
Линейная оболочка системы векторов
Пусть
![]() - система векторов из векторного
пространства V над полем P.
- система векторов из векторного
пространства V над полем P.
Определение 2: Линейной оболочкой L системы A называется множество всех линейных комбинаций векторов системы A. Обозначение L(A).
21.
СУММА И ПЕРЕСЕЧЕНИЕ ПОДПРОСТРАНСТВ
Пусть L1..Lk – линейные подпространства пространства V. Суммой подпространств L1..Lk называется множество всевозможных векторов x, представимых в виде x = x1 + … + xk, где xi из Li для любых i от 1 до k. Обозначается как L1 + L2 +.. + Lk
Представление вектора в виде такой суммы называется разложением вектора x по подпространствам L1.. Lk
Пересечением подпространств L1..Lk называется множество, в котором содержаться только те вектора, которые содержатся в каждом из подпространств L1..Lk
Пересечение пустым не бывает, как минимум это нулевой вектор.
Теорема. Сумма и пересечение подпространств линейного пространства V также является подпространством V.
Доказательство следует из определения подпространства.
Теорема. Сумма линейных подпространств есть линейная оболочка совокупности базисов слагаемых подпространств.
Доказательство – просто проверяем двустороннее вложение.
Следствие. Размерность суммы подпространств равна рангу мовокупности базисов слагаемых подпространств.
Теорема. Для любых двух подпространств выполняется равенство dim(L1+L2) = dimL1 + dim L2 – dim(L1^L2)
Доказательство.
Если пересечение ненулевое, то смотрим его базис – f1..fn – так как пересечение является подпространством каждого из исходных подпространств, этот базис можно дополнить до базиса каждого из подпространств. Дополним, получим два базиса. В каждом из них будет n векторов из базиса пересечения. А если дополнить до базиса совокупности сразу, получим n векторов из базиса пересечения и еще m и s дополняющих векторов до базиса первого и второго подпространства. То есть, m+s+n = m+n + s +n – s – верно, доказано.
22.
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Необходимость
Пусть система совместна.
Тогда существуют числа![]() такие, что
такие, что
![]() . Следовательно, столбец b является
линейной комбинацией столбцов
. Следовательно, столбец b является
линейной комбинацией столбцов
![]() матрицы A. Из того, что ранг матрицы не
изменится, если из системы его строк
(столбцов) вычеркнуть или приписать
строку (столбец), которая является
линейной комбинацией других строк
(столбцов) следует, что
матрицы A. Из того, что ранг матрицы не
изменится, если из системы его строк
(столбцов) вычеркнуть или приписать
строку (столбец), которая является
линейной комбинацией других строк
(столбцов) следует, что
![]()
Достаточность
Пусть![]() . Возьмем в матрице A какой-нибудь базисный
минор. Так как
. Возьмем в матрице A какой-нибудь базисный
минор. Так как
![]() , то он же и будет базисным минором и
матрицы B. Тогда согласно теореме о
базисном миноре последний столбец
матрицы B будет линейной комбинацией
базисных столбцов, то есть столбцов
матрицы A. Следовательно, столбец
свободных членов системы является
линейной комбинацией столбцов матрицы
A.
, то он же и будет базисным минором и
матрицы B. Тогда согласно теореме о
базисном миноре последний столбец
матрицы B будет линейной комбинацией
базисных столбцов, то есть столбцов
матрицы A. Следовательно, столбец
свободных членов системы является
линейной комбинацией столбцов матрицы
A.
24.
