Вопрос 25. Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник. Тороид можно рассматривать как длинный соленоид, свернутый в кольцо (рис. 4.1).
Рис. 4.1. Магнитное поле соленоида
Длина соленоида l содержит N витков и по нему протекает ток I. Считаем соленоид бесконечно длинным. Эксперимент показал, что внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю).
Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, охватывающему все N витков, согласно (4.12) равна:
.
(4.14)
Интеграл
можно
представить в виде суммы двух интегралов:
по внутренней части контура:
и
по внешней:
,
тогда из (4.14) получим:
,
(4.15)
или
,
(4.16)
где
В
– индукция магнитного поля внутри
соленоида;
–
число витков на единицу длины соленоида.
Магнитное поле внутри тороида, так же, как в соленоиде, однородно, сосредоточено внутри; вне тороида магнитное поле, создаваемое круговыми токами тороида, равно нулю. Величина магнитного поля в тороиде определяется выражением (4.16), причем длина тороида l берется по средней длине тороида (среднему диаметру).
Отметим любопытный факт. Во всех учебниках по физике остался не отмеченным факт существования у соленоида и тороида второго магнитного поля, которое появляется из-за того, что, например, в соленоиде по отношению к средней линии соленоида витки направлены не точно перпендикулярно, а под углом меньше 90°. Это приводит к появлению тока (эффективного, но равного току I, протекающему через соленоид), вдоль соленоида (рис. 4.2).
Рис. 4.2. Второе магнитное поле соленоида
То
есть соленоид создает дополнительное
магнитное поле, такое же, как и прямолинейный
бесконечно длинный проводник с током.
Точно так же и для тороида: вдоль средней
линии протекает эффективный ток I.
У тороида второе магнитное поле
эквивалентно магнитному полю витка с
током (рис.4.3). Диаметр этого витка равен
диаметру тороида (его средней линии), а
магнитное поле тороида
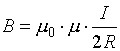(R
– радиус тороида).
Рис. 4.3. Второе магнитное поле тороида
Вопрос 26. Теорема Гаусса для магнитной индукции
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
.
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.
Вопрос 28. Электромагни́тная инду́кция. При изменении магнитного потока, пронизывающего замкнутый контур, в нем возникает электрический ток. Это явление было названо электромагнитной индукцией («индукция» означает «наведение»).
Электромагнитная индукция была открыта Майклом Фарадеем в 1831 году. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина ЭДС не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток вызванный этой ЭДС называется индукционным током.
Согласно закону электромагнитной индукции Фарадея (в системе СИ):
где
—
электродвижущая сила, действующая вдоль
произвольно выбранного контура,
ΦB — магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
—
электродвижущая сила, N — число витков,
ΦB — магнитный поток через один виток.
Векторная форма
В дифференциальной форме закон Фарадея можно записать в следующем виде:
(в системе СИ)
и
(в системе СГС).
или с помощью простейшей эквивалентной формулы:
Здесь
—
напряжённость электрического поля,
—
магнитная индукция, C
— произвольная площадка,
—
её граница.
Закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля.
Вопрос 29. Если плоская рамка площади S равномерно вращается с частотой ν оборотов в секунду в однородном магнитном поле с индукцией то магнитный поток Φ, пронизывающий рамку периодически изменяется во времени:
Φ (t) = BS cos (2πνt).
В соответствии с законом электромагнитной индукции Фарадея на концах рамки появится переменное напряжение:
инд = 2πνBS sin (2πνt).
Амплитуда этого напряжения пропорциональна скорости вращения рамки. Такая рамка, вращающаяся в магнитном поле, является моделью генератора переменного тока.
Индуктивность — физическая величина, характеризующая магнитные свойства электрической цепи.
Если в проводящем контуре течёт ток, то ток создаёт магнитное поле. Величина магнитного потока, пронизывающего контур, связана с величиной тока следующим образом: Φ = LI.
В случае катушки состоящей из N витков: Ψ = NLI,
где
L — индуктивность катушки,
— сумма магнитных потоков через все
витки. Ψ называют потокосцеплением или
полным магнитным потоком. Если поток,
пронизывающий каждый из витков одинаков,
то Ψ = NΦ.
Коэффициент пропорциональности L называется коэффициентом самоиндукции контура или индуктивностью.
В системе единиц СИ индуктивность измеряется в генри, сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109 см)
Символ L, используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
.
При
заданной силе тока индуктивность
определяет энергию магнитного поля
тока:
.
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности.
Свойства индуктивности
Индуктивность всегда положительна;
Индуктивность зависит только от геометрических свойств контура
Индуктивность соленоида
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр. При этих условиях и без использования магнитного материала плотность магнитного потока B в пределах катушки является фактически постоянной и равна
B = μ0Ni / l,
где μ0 − проницаемость вакуума, N − число витков, i − ток и l − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B, умноженному на площадь поперечного сечения S и число витков N:
Отсюда следует формула для индуктивности соленоида
Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.
При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
.
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.