Вопрос 12. Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации. В си: .

Для полного определения электромагнитного поля урравнения Максвелла необходимо дополнить материальными уравнениями, связыывающими векторы и (а также и ) в веществе. В вакууме эти векторы совпадают, а в веществе связь между ними зачастую предполагают линейной:

Величины образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. В изотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения для приобретают простой вид

Возможны среды, для которых зависимость между и является нелинейной.

Граничные условия

На границе двух веществ скачок нормальной компоненты D_n вектора определяется поверхностной плотностью свободных зарядов:

(в СГС)

(в СИ)

Здесь  — нормальная производная,  — точка на поверхности раздела,  — вектор нормали к этой поверхности в данной точке,  — поверхностная плотность свободных зарядов. Уравнение не зависит от выбора нормали (внешней или внутренней). В частности, для диэлектриков уравнение означает, что нормальная компонента вектора непрерывна на границе сред. Простого уравнения для касательной составляющей записать нельзя, она должна определяться из граничных условий для и материальных уравнений.

Вопрос 13. Теорема Гаусса для электростатического поля в диэлектрике: (3) т. е. поток вектора смещения электростатического поля в диэлектрике сквозь любую замкнутую поверхность равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности. В такой форме теорема Гаусса верна для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред. Для вакуума D_n = ε₀E_n (ε=1), и поток вектора напряженности Е сквозь произвольно выбранную замкнутую поверхность равен Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как где ∑Q_i и ∑Q_sv— соответственно алгебраические суммы свободных и связанных зарядов, которые охватываются замкнутой поверхностью S. Но эта формула неприменима для описания поля Е в диэлектрике, поскольку она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз показывает целесообразность введения вектора электрического смещения.

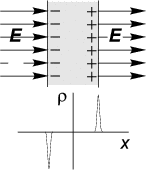
Вопрос 14. Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах — ионы, в плазме — и электроны, и ионы. Для электростатических явлений поле внутри проводника равно нулю:

E→in ≡ 0 .

Механизм исчезновения электрического поля в проводниках связан со смещением свободных зарядов ровно настолько, чтобы как раз компенсировать внешнее электрическое поле, если таковое имеется. При изменении внешнего поля свободные заряды в проводнике перераспределяются, а в момент перераспределения в проводнике течет ток. Пример такой компенсации внутри проводящей пластины изображен на рис. 1.25.

Рис. 1.25: Проводящая пластина в однородном электрическом поле и распределение плотности заряда в объёме проводника. В плазме толщина заряженного слоя на поверхности составляет несколько радиусов Дебая, в металле — несколько длин Ферми.

Поскольку E→in = 0, то и плотность заряда внутри проводника также равна нулю:

ρin = 1 4π divE→in ≡ 0.

Заряды, компенсирующие внешнее поле, могут размещаться только на поверхности проводника. В связи с этим говорят, что проводник квазинейтрален. По аналогии с объёмной плотностью заряда ρ = limΔV →0Δq∕ΔV , поверхностную плотность определяют, как предел отношения заряда на физически малом участке поверхности Δq к площади этого участка ΔS:

σ = limΔS→0Δq∕ΔS .

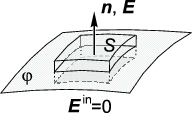
Все точки проводника имеют одинаковый потенциал, так как gradϕin = −E→in = 0. Поверхность проводника также эквипотенциальна. Следовательно, электрическое поле перпендикулярно к ней. Этот факт иногда формулируют в виде равенства нулю тангенциальной (касательной к поверхности проводника) проекции внешнего электрического поля E→t = [[n→,E→],n→]:

E→t = 0.

Здесь и далее n→ обозначает внешнюю нормаль к поверхности проводника.

Рис. 1.26: Поток через верхнюю грань параллелепипеда, натянутого на элемент поверхности S, равен En S; поток через остальные грани равен нулю. Сравнивая En S с полным зарядом 4π σ S внутри параллелепипеда, получаем граничное условие En = 4πσ.

Нормальная компонента электрического поля на поверхности проводника En = (n→,E→) однозначно связана с поверхностной плотностью зарядов. Применяя теорему Гаусса к параллелепипеду, натянутому на элемент поверхности проводника (рис. 1.26), получаем:

E→n = 4πσ .

Обычно распределение зарядов σ по поверхности проводника неизвестно. Если нужно, его находят в результате решения задачи (см. след. параграф). Однако одну существенную закономерность можно указать из качественных соображений (Б.Франклин, 1747 г.). Так как одноименные заряды (заряды одного знака) отталкиваются, они стремятся разойтись в проводнике как можно дальше. Это приводит к накоплению зарядов на наиболее удаленных участках проводников, например на остриях. Поле вблизи острия можно приближенно представить, как поле заряженной сферы того же радиуса кривизны r. Отсюда можно оценить напряженность электрического поля и поверхностную плотность заряда 4πσ ∼ E ∼ ϕ∕r, где ϕ — потенциал проводника относительно соседних тел. При этом полезно отметить, что полный заряд острия q ∼ πr2σ ∼ ϕr все-таки составляет малую долю заряда всего проводящего тела Q ∼ ϕR, где R — его характерный размер.

Вопрос 17. 1. Энергия системы неподвижных точечных зарядов. Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q₁ и Q₂, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда): где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно, и поэтому W₁ = W₂ = W и Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна (1) где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го. 2. Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна ");?>" alt="элементарная работа сил электрического поля заряженного проводника"> Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу (2) Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник: (3) Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем где Q=∑Q_i - заряд проводника. 3. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна (4) где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора. Используя выражение (4), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда (5) Подставив в (4) выражение для емкости плоского конденсатора, получим (6) Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу: где знак минус указывает, что сила F является силой притяжения. 4. Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε₀εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда (7) где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е. Объемная плотность энергии электростатического поля (энергия единицы объема) (8) Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε₀Е. Формулы (4) и (7) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля. Возникает вопрос о локализации электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика занимается изучением постоянных во времени поля неподвижных зарядов, т. е. в ней поля и попродившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на данный вопрос не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать отдельно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, которые способны переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.

Вопрос 18. Магни́тное по́ле — составляющая электромагнитного поля, появляющаяся при наличии изменяющегося во времени электрического поля. Кроме того, магнитное поле может создаваться током заряженных частиц, либо магнитными моментами электронов в атомах (постоянные магниты). Основной характеристикой магнитного поля является его сила, определяемая вектором магнитной индукции (вектор индукции магнитного поля)[1]. В СИ магнитная индукция измеряется в Тесла (Тл).

Магнитное поле — это особый вид материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

Можно также рассматривать магнитное поле, как релятивистскую составляющую электрического поля. Точнее, магнитные поля являются необходимым следствием существования электрических полей и специальной теории относительности. Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются свет и прочие электромагнитных волны.

Магнитное поле формируется изменяющимся во времени электрическим полем либо собственными магнитными моментами частиц. Кроме того, магнитное поле может создаваться током заряженных частиц.

Величина B в системе единиц СИ измеряется в теслах, в системе СГС в гауссах.

Векторное поле H измеряется в амперах на метр (А/м) в системе СИ и в эрстедах в СГС. Эрстеды и гауссы являются тождественными величинами, их разделение является чисто терминологическим.

В простых случаях магнитное поле может быть найдено из закона Био — Савара — Лапласа или теоремы о циркуляции (она же — закон Ампера). В более сложных ситуациях ищется как решение уравнений Максвелла.

Вопрос 19. Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.

Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме,  — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)

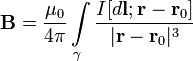
Направление перпендикулярно и , то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)

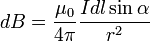
Векторный потенциал даётся интегралом (в системе СИ)

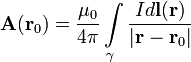
Вопрос 20. Закон Ампера — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током.

Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :

.

Если ток течёт по тонкому проводнику, то , где  — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :

.

Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

,

где α — угол между векторами магнитной индукции и тока.

Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ( ): .

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии a друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I₁ и I₂. Требуется найти силу, действующую на единицу длины проводника.

Бесконечный проводник с током I₁ в точке на расстоянии r создаёт магнитное поле с индукцией:

(по закону Био — Савара — Лапласа).

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).

Модуль данной силы (r - расстояние между проводниками):

Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1):

Вопрос 21. Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд попрождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой (1) где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r : его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.

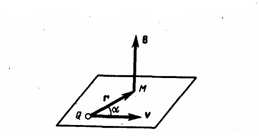
Рис.1

Модуль вектора магнитной индукции (1) находится по формуле (2) где α — угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Приведенные законы (1) и (2) выполняются лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле движущегося с постоянной скорость заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, который находится в той точке, где в данный момент времени находится движущийся заряд. Формула (1) задает магнитную индукцию положительного заряда, движущегося со скоростью v. При движении отрицательнго заряда Q заменяется на -Q. Скорость v - относительная скорость, т. е. скорость относительно системы отсчета наблюдателя. Вектор В в данной системе отсчета зависит как от времени, так и от расположения наблюдателя. Поэтому следует отметить относительный характер магнитного поля движущегося заряда. Первый, кто обнаружил поле движущегося заряда, был американский физик Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), который изучал магнитное поле конвекционного тока и магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле движущихся с постоянной скоростьб зарядов было измерено академиком А. Ф. Иоффе, который также доказал эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.