Сортировка слияниями
Прежде чем обсуждать новый метод, рассмотрим следующую задачу. Объединить ("слить") упорядоченные фрагменты массива A [k],.... А [т] и А [т 4- 1],..., A [q] в один A [k + 1], ..., A [q], естественно, тоже упорядоченный (k < т <= q). Основная идея решения состоит в попарном сравнении очередных элементов каждого фрагмента, выяснении, какой из элементов меньше, переносе его во вспомогательный массив D (для простоты) и продвижении по тому фрагменту массива, из которого взят элемент. При этом следует не забыть записать в D оставшуюся часть того фрагмента, который не успел себя "исчерпать".
Пример. Пусть первый фрагмент состоит из 5 элементов: 3 5 8 11 16, а второй — из 8: 1 5 7 9 12 13 18 20. Рисунок на с. 10 иллюстрирует логику объединения фрагментов.
Procedure SI(k,m,q:Integer); {Массив А глобальный} Var i, j, t : Integer; D:MyArray; Begin i:=k; j: =m+1; t:=l; While (i<=m) And (j<=q) Do Begin {Пока не закончился хотя бы один фрагмент.} If A[i]<=A[j] Then Begin D[t]:=A[i]; Inc( i ); End Else Begin D[t] :=A[j ]; Inc( j ); End; Inc(t); End; {Один из фрагментов обработан полностью, осталось перенести в D остаток другого фрагмента.} While i<=m Do Begin D[t]:=A[i]; Inc (i); Inc(t) End; While j<=q Do Begin D(t]:=A[j];Inc(j); Inc(t) End; For i:=l To t-1 Do A[k+I-1]:=D[i]; End;
Параметр m из заголовка процедуры можно убрать. Мы "сливаем" фрагменты одного массива А. Достаточно оставить нижнюю и верхнюю границы фрагментов, т.е. — Sl(к, q: Integer), где k — нижняя, а q — верхняя границы. Вычисление т (эта переменная становится локальной) сводится к присвоению: т:= k + (q — k) Div 2. При этом уточнении приведем процедуру сортировки. Первый вызов процедуры — Sort(1, N).
Procedure Sort(i,j:Integer); Var t:Integer; Begin If i>=j Then Exit; {Обрабатываемый фрагмент массива из одного элемента.} If j-i=l Then Begin If A[j]<A[i] Then Begin{Обрабатываемый фрагмент массива из двух элементов.} t:=A[i];A[i] :=A[j];A[j] :=A[i]; End; End Else Begin Sort (i,i+(J-i) Div 2); {Разбиваем заданный фрагмент на два.} Sort(i+(j-i) Div 2+1,j); Sl(I,j); End; End;
Метод слияний — один из первых в теории алгоритмов сортировки. Он предложен Джоном фон Нейманом в 1945 году. В этом алгоритме наглядно реализован принцип "разделяй и властвуй". Рекомендуется проделать с учащимися "ручную" трассировку работы процедуры на различных примерах. Это, во-первых, позволит в очередной раз глубже понять суть принципа и, во-вторых, проверить понимание и усвоение темы "рекурсия". Эффективность алгоритма, по Д. Кнуту, составляет С= O(N• Log2N).
Задания для самостоятельной работы
1. Дан массив 7 9 13 1 8 4 10 11 5 3 6 2. Видим возрастающий участок 7 9 13, а справа, если читать справа налево, есть участок 2 6. Слияние этих двух фрагментов массива дает 2 6 7 9 13. А затем "сливаем" 1 8 и 3 5 11, получаем 1 3 5 8 11. Записываем в массив и получаем: 2 6 7 9 13 4 10 11 8 5 3 1. Обратите внимание на то, как записываем! Продолжим. Поскольку средний участок 410 "сливать" не с чем, рассмотрим его как два — 410 и 10 (т.е. прочитаем его в двух направлениях). Если с первыми фрагментами 2 6 7 9 13 и 1 3 5 8 11 все ясно, то вторые 4 10 и 10 перекрываются. Необходимо учесть сей факт и не дублировать 10 при записи в массив. Получаем: 1 2 3 5 6 7 8 9 11 13 10 4. Последнее "слияние" дает 1 2 3 4 5 6 7 8 9 10; 11 13. Массив отсортирован. Этот метод называется у Д. Кнута “сортировкой естественным двухпутевым слиянием” 2. 'Изменим схему выбора участков для "слияния". Не будем искать монотонные участки, а работаем с участками фиксированной длинны (“простое двухпутевое слияние”). Пример. Исходный массив: 13 1 7 5 4 3 9 10 6 19 14 16 23 2 4 8. 1-й шаг (длина 1). 8 13 2 7 4 16 9 19 10 6 14 3 23 5 4 1. 2-й шаг (длина 2). 14 813 3 4 14 16 19 10 9 6 23 7 5 2. 3-й шаг (длина 4). 1 2 4 5 7 8 13 23 1916 14 10 9 6 4 3. 4-й шаг (длина 8). 1 2 3 4 4 5 6 7 8 9 10 13 14 16 19 23. Реализовать данный алгоритм сортировки. Размер массива не всегда совпадает с числом, равным степени двойки. 3. Интеграция алгоритма простых вставок с предыдущим упражнением дает новое задание. Разделим массив на участки определенной длины. Каждый из них отсортируем с помощью алгоритма простых вставок, а затем используем "простое двухпутевое слияние". Так, в предыдущем примере слияние используется на 3-м и 4-м шагах, а первые два заменяются работой по алгоритму простых вставок. 4. Обобщите предыдущие задание заменой слова “двухпутевое” на “трехпутевое“ ( “четырехпутевое” ,..., "k-путевое" ). Значительное увеличению программного кода при этом недопустимо. Примечание. В этом параграфе, как и во всех предыдущих, мы работаем с целочисленным массивом. Если использовать для хранения данных не массив, а однонаправленный или двунаправленный списки, то все задания становятся хорошей базой для изучения этих типов данных.
Быстрая сортировка
Данный метод был предложен Ч.Э.Р. Хоаром в 1962 году. В общем случае его эффективность достаточно высока (слова "в общем случае" означают, что можно специально подобрать такие наборы данных, на которых данная сортировка будет малоэффективна), поэтому автор назвал его "быстрой сортировкой". Опишем идею метода. В исходном массиве А выбирается некоторый элемент X (его называют "барьерным"). Нашей целью является запись Х "на свое место" в массиве, пусть это будет место k, такое, чтобы слева от Х были элементы массива, меньшие или равные X, а справа — элементы массива, большие X, т.е. массив А будет иметь вид: (A[1], A[2], ..., A[k - 1] ), A[k] = (X), (A[k + 1], ..., A[n] ). В результате элемент A [k] находится на своем месте и исходный массив А разделен на две неупорядоченные части, барьером между которыми является элемент А [k]. Далее требуется отсортировать полученные части тем же методом до тех пор, пока в каждой из частей массива не останется по одному элементу, то есть пока не будет отсортирован весь массив.
Пример. Исходный массив состоит из 8 элементов: 8 12 3 7 19 11 4 16. В качестве барьерного элемента возьмем средний элемент массива (7). Произведя необходимые перестановки, получим: (4 3) 7 (12 19 11 8 16); теперь элемент 7 находится на своем месте. Продолжаем сортировку. Левая часть: Правая часть: (3) 4 7 (12 19 11 8 16) 3 4 7 (8) 11 (19 12 16) 3 4 7 (12 19 11 8 16) 3 4 7 8 11 (19 12 16) 3 4 7 8 11 12 (19 16) 3 4 7 8 11 12 (16) 19 3 4 7 8 11 12 16 19 Из описания алгоритма видно, что он может быть реализован посредством рекурсивной процедуры, параметрами которой являются нижняя и верхняя границы изменения индексов сортируемой части исходного массива. Приведем процедуру быстрой сортировки (автора первоначального текста установить, по-видимому, не представляется возможным, поскольку эта процедура встречается в различных источниках):
Procedure Quicksort (m, t: Integer); Var i , j , x , w: Integer; Begin i:=m; j:=t; x:=A[ (m+t) Div'2]; Repeat While A[i]<x Do Inc(i); While A[j]>x Do Dec(j); If i<=j Then Begin w:=A[i]; A[i]:=A[j]; A[jl:=w; Inc(i); Dec(j) End Until i>j; If m<j Then Quicksort(m, j); If i<t Then Quicksort(i,t), End;
Простая процедура, но возникает "тысяча и один вопрос". Соответствуют ли результаты работы процедуры рассмотренному выше примеру, естественно, при тех же исходных данных? Оказывается, нет. Лучше, если учащиеся убедятся в этом самостоятельно. Результаты работы процедуры выглядят следующим образом (первые два столбца содержат параметры процедуры, третий — массив А):
m |
t |
A |
1 |
8 |
4 12 3 7 19 11 8 16 |
1 |
8 |
4 7 3 12 19 11 8 16 |
1 |
3 |
4 3 7 12 19 11 8 16 |
1 |
2 |
3 4 7 12 19 11 8 16 |
4 |
8 |
3 4 7 8 19 11 12 16 |
4 |
8 |
3 4 7 8 11 19 12 16 |
4 |
5 |
3 4 7 8 11 19 12 16 |
6 |
8 |
3 4 7 8 11 12 19 16 |
7 |
8 |
3 4 7 8 11 12 16 19 |
Продолжим наши
рассуждения.
В процедуре есть
сравнение
If i<=j Then <перестановка элементов A[i]
и A[j] >
Получается, что при
равенстве мы выполняем перестановку
элементов массива. Заменим условие на
следующее: i
< j. Результат
— бесконечная работа процедуры
("зацикливание"). Рекурсивный вызов
процедуры осуществляется при выполнении
условия т <
j. А если
просто вызвать? Результат не замедлит
сказаться. Произойдет переполнение
стека адресов возврата.
Цикл
repeat ... Until i>j;
работает и при i
= j, что кажется
неестественным. Заменим условие на
следующее: i
>= j.
Что произойдет? Заключительным "аккордом"
обсуждения процедуры может быть
предложение написать код, соответствующий
примеру, рассмотренному в начале
параграфа.
Оценим эффективность
метода. Предположим, что размер массива
равен числу, являющемуся степенью двойки
(N = 2q),
и при каждом разделении элемент Х
находится точно в середине массива. В
этом случае при первом просмотре
выполняется N сравнений и массив
разделится на две части размерами
N/2.
Для каждой из этих частей выполняется
N/2 сравнений и т.д. В конечном итоге
С
=
N + 2 • (N/2) + 4 • (N/4) + ... + N • (N/N) =
0(N • logN). Если N не является степенью
двойки, то оценка будет иметь тот же
порядок. Для экзотического случая — Х
на каждом шаге оказывается самым
маленьким или самым большим элементом
в рассматриваемой части массива — С =
0(N2),
ибо на каждом шаге размер сортируемой
части массива уменьшается лишь на
единицу.
Задания для самостоятельной работы 1. Следует отметить, что данный алгоритм является затратным с точки зрения использования оперативной памяти. Замените рекурсивную схему реализации логики на нерекурсивную и оцените значение N, при котором ваша программа в рекурсивной реализации не будет компилироваться по этой причине. Разумеется, такую оценку можно сделать и при рекурсивной реализации, просто тип ошибки будет другой. Вводить исходные данные с клавиатуры или вручную создавать входной файл — утомительное занятие. Разумная лень — двигатель прогресса, поэтому для выполнения задания необходимо написать специальную программу создания входного файла с данными. 2. Считается, что выбор элемента Х случайным образом оставляет среднюю эффективность неизменной при всех типах массивов (упорядоченный, распределенный по какому-то закону и т.д.). Реализуйте эту идею.
Пирамидальная сортировка Данный метод был предложен Дж.У.Дж. УИЛЬЯМСОМ и Р.У. Флойдом в 1964 году. Элементы массива А образуют пирамиду, если для всех значений i выполняются условия: A [i] <= А [2 • i] и А [i] <= А [2 • i + 1 ].
Пример. Элементы массива 8 10 3 6 13 9 5 12 не образуют пирамиду (А[1] > А [3], А [2] > А [4] и т.д.), а элементы массива 3 6 5 10 13 9 8 12 — образуют. Очевидно, что элементы правой половины массива A [N/2+1 .. N] независимо от их значений образуют пирамиду. Предположим, что нам необходимо отсортировать элементы массива А (8 10 3 6 13 9 5 12) по невозрастанию. Идею сортировки поясним с помощью следующей таблицы (курсивом выделена часть элементов массива, образующих пирамиду, жирным шрифтом — отсортированная часть массива).
№ шага |
A |
Комментарии |
1 2 3 4 5 |
8 10 3 6 13 9 5 12 8 10 3 6 13 9 5 12 8 10 3 6 13 9 5 12 8 6 3 10 13 9 5 12 3 6 5 10 13 9 8 12 |
Строим пирамиду из элементов A с1-го по 8-й |
6 |
12 6 5 10 13 9 8 3 |
Меняем местами 1-й и 8-й элементы |
7 8 9 10 |
12 6 5 10 13 9 8 3 12 6 5 10 13 9 8 3 12 6 5 10 13 9 8 3 5 6 8 10 13 9 12 3 |
Строим пирамиду из элементов A с 1-го по 7-й |
11 |
12 6 8 10 13 9 5 3 |
Меняем местами 1-й и 7-й элементы |
12 13 14 15 |
12 6 8 10 13 9 5 3 12 6 8 10 13 9 5 3 12 6 8 10 13 9 5 3 6 10 8 21 13 9 5 3 |
Строим пирамиду из элементов A с 1-го по 6-й |
16 |
9 10 8 12 13 6 5 3 |
Меняем местами 1-й и 6-й элементы |
17 18 19 |
9 10 8 12 13 6 5 3 9 10 8 12 13 6 5 3 8 10 9 12 13 6 5 3 |
Строим пирамиду из элементов A с 1-го по 5-й |
20 |
13 10 9 12 8 6 5 3 |
Меняем местами 1-й и 5-й элементы |
21 22 23 |
13 10 9 12 8 6 5 3 13 10 9 12 8 6 5 3 9 01 13 12 8 6 5 3 |
Строим пирамиду из элементов A с 1-го по 4-й |
24 |
12 10 13 9 8 6 5 3 |
Меняем местами 1-й и 4-й элементы |
25 26 |
12 10 13 9 8 6 5 3 10 12 13 9 8 6 5 3 |
Строим пирамиду из элементов A с 1-го по 3-й |
27 |
13 12 10 9 8 6 5 3 |
Меняем местами 1-й и 3-й элементы |
28 29 |
13 12 10 9 8 6 5 3 12 13 10 9 8 6 5 3 |
Строим пирамиду из элементов A с 1-го по 2-й |
30 |
13 12 10 9 8 6 5 3 |
Меняем местами 1-й и 2-й элементы |
В конечном итоге массив отсортирован. Пусть мы умеем строить пирамиду из элементов массива А с индексами от 1 до q (процедура Руram (q) ), тогда процедура сортировки имеет вид:
Procedure Sort; Var t,w:Integer; Begin t:=N; Repeat Pyram(t);{Строим пирамиду из t элементов.} w:=A[1];A[1]:=A[t];A[t]:=w; Dec (t) Until t<2 End;
Из таблицы мы видим, что процесс построения пирамиды начинается с конца массива. Посдедние q div 2 элементов являются пирамидой по той причине, что удвоение индекса выводит нас за пределы массива. А затем берется очередной справа элемент из "непирамидальной" части и "проталкивается" по "пирамидальному" массиву до тех пор, пока он не будет меньше элемента с удвоенным индексом (по отношению к индексу рассматриваемого элемента) и следующего за ним элемента. Процесс продолжается до тех пор, пока мы "не поставим" на своё место первый элемент массива. Приведем текст процедуры.
Procedure Pyram(q:Integer); Var r, i, j,v:Integer; Begin r:=q Div 2+1;{Эта часть массива является пирамидой.} While г>1 Do Begin{Цикл-по элементам массива, для которых необходимо найти место в пирамиде.} Dec(г); i:=r; v:=A[i];{Индекс, рассматриваемого элемента и сам элемент.} j:=2*i;{Индекс элемента, с которым происходит сравнение.} pp:=False;{Считаем, что для элемента не найдено место в пирамиде.} While (J<=q) And Not pp Do Begin If j<q Then If A[j]>A[j+l] Then Inc(j);{Сравниваем с меньшим элементом.} If v<=A[j] Then pp:=true {Элемент находится на своем месте.} else begin A[i]:=A[j]; i:=j; j:=2*i end {Переставляем элемент и идем дальше по пирамиде.} End; A[i]:=v End; End;
Метод имеет эффективность порядка O(N • logN). Однако если рассмотреть вышеприведенную логику, то окажется, что ее оценка O(N2 • logN). При сортировке процедура Pyram вызывается N — 1 раз. Эта процедура состоит из двух вложенных циклов сложности N и — logN. Итак, упорядочивание одного элемента требует не более logN действий, построение полной пирамиды N • logN действий. В вышеприведенной логике после каждой перестановки элементов вновь строится пирамида для оставшихся элементов массива. А зачем? Пирамида почти есть. Требуется только "протолкнуть" верхний элемент на свое место (т.е. строки таблицы с номерами 7—9, 12—14, 17—18,21—22, 25, 28, вообще говоря, избыточны). Выделим "проталкивание" одного .элемента в отдельную процедуру Pr (r,q) , где r — номер проталкиваемого элемента, q — верхнее значение индекса.
Procedure Рг(r,q:Integer); Var r, i, j,v: Integer; pp:boolean; Begin i:=r; v:A[i];{Индекс рассматриваемого элемента и сам элемент.} j:=2*i;{Индекс элемента, с которым происходит сравнение.} pp:=False;{Считаем, что для элемента не найдено место в пирамиде.} While (j<=q) And Not pp Do Begin If j<q Then If A[j]>A[j+l] Then Inc(j);{Сравниваем с меньшим элементом.} If v<=A[j] Then pp:=true {Элемент находится на своём месте. } else begin A[i] :=А[j]; i:=j; j:=2*i end {Переставляем элемент и идем дальше по пирамиде.} End; A[i]:=v End;
Какие изменения требуется внести в процедуру Sort? Procedure Sort; Var t, w, i:Integer; Begin t:=N Div 2+1; {Эта часть массива является пирамидой.}; For i:=t-l DownTo 1 Do Pr(i,N);{Строим пирамиду(только один раз).} For i:=N DownTo 2 Do Begin ; w:=A[1] ;A[1]:=A[i] ;A[i]:= w; {Меняем местами 1-й и i-й элементы.} Pr(1,i-l) {Проталкиваем 1-й элемент.} End End;
Примечйние. Понижение сложности алгоритма N^2 • logN до N• logN может быть предметом самостоятельной работы с элементами соревнования.
Задания для самостоятельной работы
1.
Изменить алгоритм так, чтобы элементы
массива А сортировались в порядке
неубывания.
2. Представим
элементы нашего массива в виде бинарного
дерева так, как показано на левой части
рисунка. В результате построения пирамиды
на элементах массива с 1-го по 8-й дерево
преобразуется к виду, показанному на
Правой части рисунка. После этого
меняется содержимое определенных узлов
дерева и верхний элемент "проталкивается"
по пирамиде. Продолжите эти рисунки для
всех оставшихся шагов сортировки.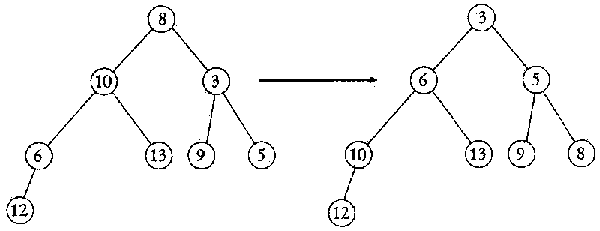
3. Разработать программу пирамидальной сортировки для случая, когда для хранения данных используется не массив, а бинарное дерево. 4. Для хранения данных используется не массив, а список (однонаправленный или двунаправленный) .— "сортировка списка". Разработать программу пирамидальной сортировки для этого случая. 5. Приведем разбор задачи "Дворец черепашек". Рекомендуется первоначально предложить ребятам решить ее самостоятельно, а затем обсудить и разобрать с учащимися.
Условие задачи. Много, очень много черепашек живет в огромном дворце со всеми удобствами, кроме одного. Им приходится ползать за водой к родниковому источнику. Дорога до источника прямая, ее длина М метров. В некоторый момент времени на дороге находится N черепашек. Часть из них ползет в сторону дворца, часть — к источнику. Все черепашки ползут с одинаковой скоростью (1 метр в час). Требуется найти: • общее количество встреч черепашек в пути; • время последней встречи. Входные данные (файл Input.Txt). В первой строке записаны значения М и N, а затем N строк, в каждой из которых записаны Х i (1 <= i<= N) — координата черепашки и буква "Д" или "И" (направление движения черепашки). Все координаты X i — вещественные числа и различны. Выходные данные (файл OutputTxt). В первой строке записывается количество встреч, во второй — время последней встречи (с точностью до пяти знаков). При отсутствии встреч выводится сообщение: "NO MEETINGS". Ограничения. 1<= N<= 30 000, время решения — 10 секунд.
Идея решения основана на сортировке массива координат черепашек с одновременной перестановкой соответствующих признаков "Д" и "И". Затем для решения первой проблемы необходимо подсчитать для каждой черепашки, ползущей к источнику, число черепашек, имеющих большее значение координаты и ползущих во дворец. Сумма этих значений является ответом. Для ответа на второй вопрос необходимо найти самую правую черепашку, ползущую к источнику, и самую левую, возвращающуюся во дворец. Расстояние между ними, деленное на два, дает время последней встречи. Итак, задачу нельзя назвать особенно сложной. Рассмотрим программную реализацию алгоритма.
Максимальное количество координат 30 000, причем вещественных значений. А это 4 байта, умноженные на 30 000, или 120 000 байт. При стандартной реализации в системе программирования Паскаль оперативной памяти явно не хватит, для задачи в качестве сегмента данных выделяется несколько меньше 64 Кб, поэтому необходимо использовать "кучу" (область оперативной памяти для динамических переменных). Объем "кучи" позволяет это сделать. Второе соображение при выборе алгоритмаследует из ограничений на время решения задачи. Алгоритмы с квадратичной эффективностью не подходят, но мы знаем три алгоритма со сложностью O(N• logN). Более эффективные мы не изучали. Учитывая этот факт и первое соображение, выбираем алгоритм пирамидальной сортировки, причем данные о местоположении черепашек — координаты следует размещать в "куче".
Структуры данных.
Const MaxN=30000; Trg=12; {212 - размер блока, для хранения всех возможных координат черепашек потребуется 8 блоков (последний используется на одну треть).} Eps=le-6;{Точность вычислений.} InputFile='Input.TxT' ; OutputFile='Output.TxT' ; _NoMeet='NO MEETINGS'; TypeBMas=Array[0..4095] Of Real; TukReal=^Real; Var A: Array[0..(MaxN-1) Div 4095] Of ^BMas; {Массив указателей (8 элементов) на блоки по 4096 вещественных чисел.} Ind: Array[O..MaxN-l] Of Char;{Направления движения черепашек.} N, sca: Word;{Количество черепашек и та их часть, которая ползет ко дворцу.} rsa: LongInt;{Ответ на 1-й вопрос.} М, rsb: Real;{Расстояние и ответ на 2-й вопрос.} rs: Boolean;{Признак того, что есть решение.}
Приведем вначале процедуру вывода результатов и основную программу, чтобы было ясно, к чему мы стремимся.
Procedure Done; Begin Assign(Output, OutputFile) ; Rewrite(Output) ; If rs Then Begin WriteLn (rsA); WriteLn (rsB: 0:5) End Else WriteLn(_NoMeet); Close(Output) End; Begin Init; Solve; Done End.
Прежде чем уточнять логику, научимся работать с массивом координат черепашек А. Функция чтения элемента из массива А по его номеру имеет вид:
Function GetA(p: Word): Real; Begin GetA:=A[p shr TRg]^[p And (4095)] {p делим на 212 (сдвиг вправо на 12 разрядов) и выделяем из р 12 младших разрядов.} End;
Запись вещественного числа в массив А программируется аналогичным образом.
Procedure SetA(p: Word; Const aa: Real); Begin A[p shr TRg]^[p And (4095)]:=aa End;
Теперь мы можем привести процедуру Init.
Procedure Init; Var i: Integer; bb: Real; Begin FillChar(A, SizeOf(A), 0) ; sca:=0; Assign(Input, InputFile) ; Reset(Input) ; Read(M, N); Dec(N); For i:=Q To N Do Begin If A[i shr TrG]=nil Then New(A[i shr TrG]) ; Read(bb) ; SetA(i, bb); Read(Ind[i]) ; While Not (UpCase(Ind[i] ) In [ 'Д', 'И' ] ) Do Read (Ind[i]) ; If Ind[i]='Д' Then Inc(sca) {Общее количество черепашек, ползущих во дворец.} End; Close(Input) End;
Обмен значениями двух элементов массива А с одновременной перестановкой соответствующих элементов массива Ind имеет вид (используется в процедуре сортировки):
Procedure SwapDD (Const ас, bc: Word); Var aa, bb: TukReal; с: Real; cc: Char; Begin aa:=@A[ac shr TRg]^[ac And (4095)];{B переменной аа адрес элемента массива, данный прием позволяет сократить длину записи последующих операторов.} bb:=@A[bc shr TRg]^[bc And (4095)]; с:=аа^; аа^:=bb^; bb^:=c; cc:=Ind[ac]; Ind[ac] :=Ind[bc]; Ind[bc] :=cc End;
Процедуру пирамидальной сортировки (Sort) приводить не будем, она описана выше. Следует только помнить, что для сравнения вещественных чисел лучше использовать функцию типа:
Function More (Const a, b: Real): Boolean; Begin More:=a-b>Eps End; Перейдем к основной процедуре. Procedure Solve; Begin Sort;{Пирамидальная сортировка.} CheckA;{Решение 1-й части задачи.} If (sca=0) Or (sca=N+l) Or (rsA=0) Then rs:=False {Heт черепашек, ползущих ко дворцу, нет черепашек, ползущих к источнику, нет ни одной встречи между черепашками. В любом из этих случаев нет решений и необходимо выводить соответствующее сообщение.} Else Begin rs:=True;CheckB End {Решаем 2-ю часть задачи.} End;
Процедура решения первой части задачи имеет вид:
Procedure CheckA; Var i, lfa: LongInt; Begin rsА:=0; 1fa:=sca;{Текущее значение количества черепашек, ползущих во дворец.} For i:=0 То N Do If Ind[i]='Д' Then Dec (lfa) {Черепашки, ползущие к источнику и находящиеся ближе к источнику, чем эта черепашка, ползущая во дворец уже не встретятся с ней.} Else lnc (rsA, Ifa) {Если черепашка ползет к источнику, то она встречается со всеми черепашками, находящимися ближе ее к источнику и ползущими во дворец.} End; Для второй части задачи процедура выглядит еще проще.
Procedure CheckB; Var i: LongInt; If, rg: Real; Begin i:=0; While Ind[i]='Д' Do Inc(i);{Находим координаты 1-й черепашки, ползущей к источнику.} if:=GetA(i); i:=N; While Ind[i]='И' Do Dec(i);{Находим координату последней черепашки, ползущей во дворец.} rg:=GetA(i); rsB:=,(rg-lf)/2 End;
Цель достигнута. Решение есть, но тема отнюдь не исчерпана. Продолжим ее обсуждение. Очевидным является шаг по замене пирамидальной сортировки на метод Хоара или слияния. А затем? Пусть каждая черепашка ползет со своей скоростью, допустим, возраст у них разный. Если до этого мы решали задачу для регулярной структуры (левая часть рисунка) — угловой коэффициент у всех прямых одинаковый, то при данной модификации задача соответствует структура, изображенная на правой части рисунка.
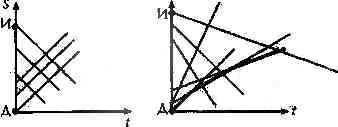На правой части рисунка более "жирными"
линиями выделена ломаная, проходящая
по участкам прямых, соответствующих
черепашкам, ползущим из дворца.
Требуется найти самую правую точку
пересечения прямых, описывающих
перемещения черепашек от источника к
дворцу, с этой ломаной.
Продолжим
наши рассуждения о задаче (усложнения).
Пусть нет черепашек, ползущих от
источника, а черепашки, достигающие
источника, остаются у него и пьют воду
не один раз, а с некоторой периодичностью
(для каждой черепашки она своя). При этом
каждая черепашка за каждый подход пьет
разное количество воды. Например, имеются
две черепашки. Первая пьет 7, 5, 3, 1 литров
воды, с периодичностью в 6 единиц времени,
вторая — 11, 7, 3, с периодичностью 5 единиц
времени. Известно количество воды в
источнике (V). Определить, какая из
черепашек будет пить последней, если
воды в источнике, не хватит, или количество
оставшейся в источнике воды для случая,
когда все черепашки могут удовлетворить
свою жажду.
Цель наших модификаций
(рассуждении) сводится к следующему:
во-первых, в оперативной памяти (включая
"кучу" ) не должно хватать места
для хранения всех данных, во-вторых, из
всех алгоритмов сортировки с эффективностью
O(N • logN) придется использовать только
пирамидальную сортировку.
Попытаемся рассмотреть возможные схемы
решения задачи. Первый вариант. Просчитаем
все значения времени питья черепашек,
а затем отсортируем и выполним требуемый
подсчет. Оперативной памяти не хватит.
Второй вариант. Можно хранить для каждой
черепашки только время ее очередного
питья, выбирать минимальное значение
и корректировать массив времен. Сложность
решения порядка О(N2),
оно не должно проходить по временным
ограничениям. Третий вариант. Хранить
упорядоченный массив времен. Брать
первый элемент — минимальный, а затем
с использованием бинарного поиска
вставлять очередной элемент. В этом
случае потребуется сдвиг элементов
массива, и окончательная оценка сложности
имеет порядок О(N2).
Четвертый вариант. Хранить данные по
временам питья черепашек в виде пирамиды.
После изъятия верхнего элемента время
следующего приема воды для этой черепашки
проталкивается по пирамиде. Этот вариант
не требует дополнитадаюй памяти и имеет
сложность O(N • logN).
Примечание. На данном примере мы старались показать процесс работы над задачей, от ее простого варианта (а мы начали не с самого простого) до олимпиадного уровня.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ:
фрагменты программ для доработки и /или поиска ошибок
написание небольших проектов демонстрирующих использование компонентов