Построение кривых
Ниже приведено построение наиболее наиболее употребительных кривых. На картинке приведена кривая и сохранены все построения. Ниже описан алгоритм построения кривой.
Лекальные кривые
Построение синусоиды
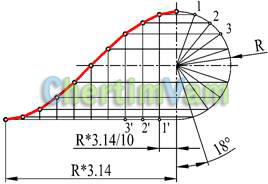
Рисунок 3 - Построение синусоиды
Синусоидой называется плоская кривая, графически изображающая изменение синуса в зависимости от его аргумента (угла). Для построения синусоиды окружность радиуса R делят на произвольное количество равных частей. На горизонтальной прямой откладывают отрезок, равный половине длины окружности (R*3.14), и делят его на такое же число равных частей. Из концов этих отрезков (точки 1',2',3') проводят вертикальные прямые до пересечения с горизонтальными прямыми, исходящими из концов соответствующих радиусов (точки 1,2,3).
Построение циклоиды
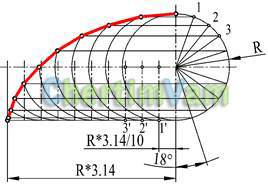
Рисунок 4 - Построение циклоиды
Циклоидой называется кривая, образованная точкой окружности, катящейся без скольжения по прямой линии. Для построения циклоиды окружность радиуса R делят на произвольное количество равных частей. На горизонтальной прямой откладывают отрезок, равный половине длины окружности (R*3.14), и делят его на такое же число равных частей. Из концов этих отрезков (точки 1',2',3') проводят вертикальные прямые до пересечения с горизонтальной осевой линией. Эти точки будут центрами окружностей радиуса R. Пересечения окружностей с соответствующими горизонтальными прямыми, исходящими из концов радиусов (точки 1,2,3), дадут точки циклоиды.
Построение эвольвенты
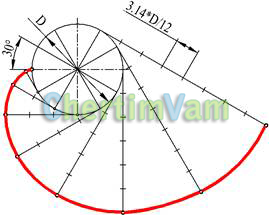
Рисунок 5 - Построение эвольвенты
Эвольвентой окружности называется кривая, которую описывает точка прямой линии, катящейся без скольжения по неподвижной окружности. Окружность диаметра D делят на произвольное число равных частей. Из точек деления проводят касательные к окружности, на которых откладывают соответственно 1, 2, 3 и т.д. части окружности.
Построение параболы
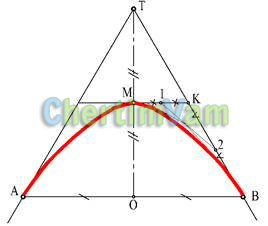
Рисунок 6 - Построение параболы
Параболойназывается, кривая, полученная при пересечении конуса и плоскости, параллельной образующей конуса. При задании параболы граничными точками А и В и точкой пересечения касательных Т кривая строится методом пропорционального деления.
Отрезок АВ делится пополам в точке О, отрезок ОТ – тоже пополам в точке М, отрезок МК - в точке 1, КВ - в точке 2 и т.д.
Построение эллипса
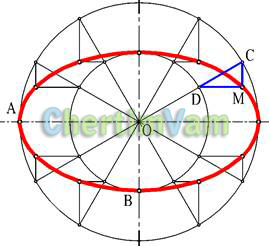
Рисунок 7 - Построение эллипса
Эллипсомназывается кривая, полученная при пересечении конуса и плоскости, пересекающей все образующее конуса.
Эллипс удобнее стоить по его полуосям (большой ОА и малой ОВ).
Для построения эллипса проводятся две соосные окружности радиусами ОВ и ОА Проведение произвольной прямой ОС и дальнейшее построение ”ключа” (треугольника СDМ со сторонами параллельными осям эллипса) позволяет определить положение текущей точки эллипса М.
Построение поверхностей
Типы моделей. Полигональные сетки
Полигональная сетка (англ. polygon mesh) или неструктурированная сетка это совокупность вершин, ребер и граней которые определяют форму многогранного объекта в трехмерной компьютерной графике и объемном моделировании. Гранями обычно являются треугольники, четырехугольники или другие простые выпуклые многоугольники (полигоны), так как это упрощает рендеринг, но так же может состоять из наиболее общих вогнутых многоугольников, или многоугольников с дырками. Учение о полигональных сетках это большой подраздел компьютерной графики и геометрического моделирования. Разные представления полигональных сеток используются для разных целей и приложений. Множество операций проводимых над сетками могут включать Булевую алгебру, сглаживание, упрощение и многие другие. Сетевые представления, такие как "потоковые" и "прогрессивные" сетки, используются для передачи полигональных сеток по сети. Объемные сетки отличаются от полигональных тем, что они явно представляют и поверхность и объем структуры, тогда как полигональные сетки явно представляют лишь поверхность (объем неявный). Так как полигональные сетки широко используются в компьютерной графике, также существуют алгоритмы трассировки лучей, обнаружения столкновений и динамики твердых тел для полигональных сеток.
Модели по их назначению бывают познавательными, прагматическими и инструментальными.
Познавательная модель — форма организации и представления знаний, средство соединения новых и старых знаний. Познавательная модель, как правило, подгоняется под реальность и является теоретической моделью.
Прагматическая модель — средство организации практических действий, рабочего представления целей системы для ее управления. Реальность подгоняется под некоторую прагматическую модель. Это, как правило, прикладная модель.
Инструментальная модель — средство построения, исследования и/или использования прагматических и/или познавательных моделей. Познавательные модели отражают существующие, а прагматические — хоть и не существующие, но желаемые и, возможно, исполнимые отношения и связи.
По уровню моделирования модели бывают эмпирическими, теоретическими и смешанными.
Эмпирическая — на основе эмпирических фактов, зависимостей;
Теоретическая — на основе математических описаний;
Смешанная или полуэмпирическая — использующая эмпирические зависимости и математические описания.
Проблема моделирования состоит из трех задач:
построения модели (эта задача менее формализуема и конструктивна, в том смысле, что нет алгоритма для построения моделей);
исследования модели (эта задача более формализуема, имеются методы исследования различных классов моделей);
использования модели (конструктивная и конкретизируемая задача).
Моделирование
— это универсальный метод получения, описания и использования знаний. Оно используется в любой профессиональной деятельности. В современной науке и технологии математическое моделирование усиливается, актуализируется проблемами, успехами других наук. Математическое моделирование реальных и нелинейных систем живой и неживой природы позволяет перекидывать мостики между нашими знаниями и реальными системами, процессами, в том числе и мыслительными.
Моделирование
- процесс построения, изучения и применения моделей.
Приведем наиболее важные типы моделей (моделирования) с краткими определениями, примерами.
Модель называется статической, если среди параметров, участвующих в описании модели, нет временного параметра. Статическая модель в каждый момент времени дает лишь «фотографию» системы, ее срез.
Примеры современных графических систем
Современные графические системы позволяют вмешиваться в процесс визуализации, используя шейдеры, что позволяет программировать достаточно гибкие и быстрые графические приложения.
Видеокарта – это сложное многофункциональное звено из всех компонентов компьютера. По другому ее также еще называют видеоплата, видюха, видеоадаптер. На ее «плечи» ложатся такие задачи, как обработка и вывод на экран монитора изображения. Видеоплата обладает собственной оперативной памятью и не зависит от основной.
В последнее время многие системные платы идут с встроенным видеоядром и исходя из этого покупать отдельно видеокарту нет необходимости.
Все пользователи ПК делятся на две группы: 1. Пользователи, работающие с офисными приложениями, Интернетом, простой графикой, прослушиванием музыки – для них качество видеокарты стоит не на первом месте; 2. Пользователи-любители компьютерных игр и профессиональные дизайнеры – для них вопрос качества видеокарты просто жизненно необходим.
Цифро-аналоговый преобразователь. (Random Access Memory Digital to Analog Converter) – это микросхема цифро-аналогового преобразования, отвечающая за вывод изображения на экран, т.е. за правильность и насыщенность цветов и за четкость изображения. RAMDAC на плате может быть несколько – отдельный чип можно установить для поддержки выхода на монитор или для видеовыхода.
От частоты работы RAMDAC зависят три параметра видеорежима:
разрешение картинки (максимальное количество по горизонтали и вертикали);
частота вертикальной развертки (Гц);
количество отображаемых цветов (16-битный или 24 (32)-битный цвет.
Как правило, мощная видеокарта, предназначенная для современных 3D-игр оснащена мощным процессором и большим объемом оперативной памяти. Создание объемного реалистичного изображения задача не простая, и для хранения одних только текстур нужен объем собственной оперативной памяти до 256 Мб. Также имейте ввиду спецэффекты в играх. Для поддержки всей этой красоты в процессор видеокарты встраивают специальный блок – «Блок трансформации и освещения» (T&L). Это позволяет получить превосходное качество игрового изображения, но тут имеется недостаток – цена платы вырастает на несколько десятков долларов.
У видеокарты имеется еще одна замечательная функция – вывод изображения на экран телевизора или прием видеосигнала с видеомагнитафона, камеры или телевизионной антенны (эту функцию выполняют видеовход и ТВ-тюнер). В связи с этим у видеоплаты появляется еще одна функция – обработка мультимедиа-информации. Более этого современным видеокартам свойственно сегодня заниматься еще и декодированием «сжатого» видеосигнала, поступающего с DVD-привода.
Чипсет. Видеоплата как и материнская плата имеет свой «мозговой центр» - специальная микросхема, графический чип, объединяющий в себе «подразделения», ответственные за работу с двухмерной и трехмерной графикой.
Производительность плат в трехмерных играх характеризуют две величины:
количество треугольников или пикселей, составляющие сложное графическое изображение, которые способна прорисовать плата в секунду;
количество кадров, сменяющихся на экране в секунду (fps – frame per second) в трехмерной игре.
Чем мощнее видеоплата, тем больше количество fps. На скорость также влияет и тип используемого процессора, цветовой режим, а также использование различных спецэффектов.
Графические диалоговые системы.
Графические возможности текстовых процессоров Большинство текстовых процессоров имеют разнообразные возможности по управлению графическими изображениями: --- импорт графики (вставить рисунок) --- вклеивание графики (через буфер обмена) --- связывание графики (диаграммы, связанные данными в таблице с помощью программы Chart) --- размещение графики на странице текстового процессора (орбамление текстом) --- водяные знаки --- слои --- изменение размера графики --- вырезание графики --- экспорт графики