2. Метод деления отрезка пополам при одномерном поиске унимодальных функций

Шаг 1. Положить и . Вычислить значение .

Шаг 2. Положить и . Точки делят отрезок на четыре равные части. Вычислить значения и .

Шаг 3. Сравнить и . Если , исключить интервал , положив (рис. 5.1.3, а). Средней точкой нового интервала поиска становится точка . Следовательно, необходимо положить . Перейти к шагу 5. Если (рис. 5.1.3, в), перейти к шагу 4.

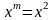Шаг 4. Сравнить и . Если , исключить интервал , положив (рис. 5.1.3, б). Так как средней точкой нового интервала становится точка , положить . Перейти к шагу 5. Если , то исключить интервалы , (рис. 5.1.3, в) и положить и . Заметим, что продолжает оставаться средней точкой нового интервала. Перейти к шагу 5.

Шаг 5. Вычислить . Если величина мала, закончить поиск. В противном случае вернуться к шагу 2.

№22

1. Полиграммы. Оценка "К ближайших соседей"

Кусочно-постоянная оценка называется полиграммой первого порядка.

Высота каждого -го прямоугольника, опирающегося на выборочный интервал ( ), равна величине

, .

2. Метод золотого сечения

,

минимизируемая функция , .

Если 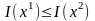, то принимается , , .

Если же , то , , .

По заданной величине 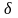точности поиска из равенства вычисляется необходимое число шагов .

№23

1. Оценка Розенблатта-Парзена.

под знак суммы этой оценки входит селектирующее прямоугольное ядро

,где

Ядро симметричное, и площадь под кривой равна единице

2. Поиск глобального минимума (метод ломанных)

Минимизируемая известной константой :

выбираем исходную точку . Находим в ней кусочно-ломаную и минимизируем ее при . Получаем . В ней опять находим и вычисляем = . Кусочно-линейная функция ограничивает снизу. Минимизация дает следующую точку . В ней также находим , а затем = . Минимизируем ее и получаем

Если длина наибольшего подынтервала в подмножестве меньше , то поиск можно прекратить

№24

2. Последовательный симплексный метод поиска экстремума функций

Шаг 1. Задается исходная вершина симплекса , размер симплекса и строится симплекс.

Шаг 2. В вершинах симплекса вычисляется минимизируемая функция .

Шаг 3. Осуществляется проверка выполнения условий окончания поиска оптимума:

. Поиск завершается, когда или размеры, или разности между значениями функции в вершинах становятся достаточно малы. При выполнении условия процесс поиска заканчивается. Решением задачи (с выбранной точностью) является: – точка с минимальным значением функции .

Если неравенство не выполняется, то осуществляется перемещение к оптимуму за счет перехода одного симплекса к другому.

Шаг 4. Находится наихудшая вершина симплекса. Эта вершина с максимальным значением .

Вычисляется центр тяжести противоположной грани:

.

Шаг 5. Осуществляется отражение вершины относительно :

,

и в точке вычисляется функция .

Шаг 6. Если точка оказывается хуже всех остальных точек нового симплекса, то осуществляется возврат к прежнему симплексу с последующим его сжатием относительно лучшей из вершин :

симплекса: Здесь – коэффициент сжатия симплекса. Осуществляется переход к шагу 2.

Если же точка 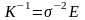не является "худшей" в новом симплексе, то продолжается дальнейшее движение (переход к шагу 4)

№25

1) Оценки условной вероятности (Розенблатта-Парзена)

.

Подставляем оценки Розенблатта

= .

Колоколообразная функция

по форме повторяет ядро и отличается от него на нормирующий множитель . За счет этого .

2) Метод деформируемого многогранника. (Нелдера-Мида)

.Процедура отыскания вершины с меньшим значением состоит из следующих операций.

1. Отражение вершины через центр тяжести противоположной грани: ,

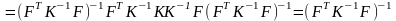2. Растяжение. Если оказывается что , то вектор растягивается: , где – коэффициент растяжения (рис. 5.4.1, б). Если , то заменяется на и процедура продолжается снова с операции 1 при . Если же , то 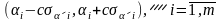заменяется на и также осуществляется переход к операции 1 при .

3. Сжатие. Если для всех , то вектор сжимается: , где – коэффициент сжатия. Затем заменяется на и осуществляется возврат к операции 1 для продолжения поиска на -м шаге.

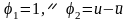4. Редукция. Если , то все векторы , , уменьшаются в раз (например, в 2 раза) в соответствии с формулой и осуществляется возврат к операции 1 (к+1). Критерий окончания поиска может иметь вид .

№26