1)Насыщенные планы. Симплекс.

Правильным симплексом называется выпуклая правильная фигура в многомерном пространстве, число вершин которой превышает размерность этого пространства на единицу.

Эти планы центральные и ортогональные.

Приведём для разнообразия один из общих способов построения планов:

2) Робастные оценки статистических параметров

есть среднее арифметическое измеренных значений выхода:

Для расчета параметров применим метод последовательной линеаризации. Вначале находим квадратичную аппроксимацию функционала относительно траектории ( ), на которой он построен:

а) , б) , в) (6.5.4)

Теперь подставим в правую часть уравнения (в квадратичный функционал) линейную аппроксимацию выхода модели

и решаем обычную задачу наименьших квадратов

№16

1) Разбиение матрицы планирования на блоки

Считаем, что выход объекта имеет аддитивный дрейф на величину (когда проводятся эксперименты с номерами 1, 2, 3, 4) и на величину (когда проводятся эксперименты № 5, 6, 7, 8). Этот дрейф приводит к смещению на величину параметра :

.

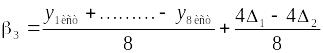						Номер блока
1	+	+	+	+		1
2	–	+	+	–		2
3	+	–	+	–		2
4	–	–	+	+		1
5	+	+	–	–		2
6	–	+	–	+		1
7	+	–	–	+		1
8	–	–	–	–		2

Введем дрейфовую переменную и по ней получим 2 блока (табл. 3.8.2). Каждый блок представляет собой дробную реплику.

Таблица 3.8.2 

1	+	+	+	+
2	–	–	+	+		Блок 1
3	–	+	–	+
4	+	–	–	+
5	–	+	+	–
6	+	–	+	–		Блок 2
7	+	+	–	–
8	–	–	–	–

№17

1. Обработка результатов эксперимента

1. Проверка однородности дисперсий

2. Проверка адекватности модели

3. Проверка значимости коэффициентов Если статистика Стьюдента лежит внутри интервала (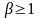 ), то принимается гипотеза о том, что коэффициент модели незначимо отличается от нуля.

4. Интерпретация модели

2) Адаптивные алгоритмы подстройки параметров статистических моделей объектов

меняются лишь весовые коэффициенты для моментов измерений. Эти же весовые коэффициенты переходят и в алгоритмы адаптивной перестройки параметров

, ,

.

№19

1. Ротатабельное планирование

Если дисперсия одинакова на равном удалении от центра плана, то такой план называется ротатабельным. Ортогональный план первого порядка является ротатабельным. равна величине . Здесь , – квадрат расстояния от точки 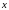до начала координат

Композиционный план второго порядка можно сделать ротатабельным планом. Если ядром плана служит полный факторный эксперимент (т. е. ), то , а если ядром служат дробные реплики ( ), то .