
- •1)Общая схема проверки гипотез
- •2) Постановка задачи адаптивного управления
- •1)Проверка гипотезы о математическом ожидании
- •1)Байесова теория принятия решений при непрерывных признаках
- •2)Подстройка параметров с использованием чувствительности
- •1) Идея классификации
- •2) Подстройка параметров динамических моделей с использованием итеративных моделей
- •Прямые методы восстановления решающей функции
- •1)Насыщенные планы. Симплекс.
- •1) Разбиение матрицы планирования на блоки
- •Адаптивные подстройки параметров не линейной статистической модели
- •1) Ортогональное планирование второго порядка
- •2) Простейший адаптивный алгоритм подстройки параметров
- •Метод случайного баланса
- •Многоэтапный метод селекции при построении моделей сложных объектов
- •Простейшие оценки плотности распределения и функции распределения.
- •Метод деления отрезка пополам при одномерном поиске унимодальных функций
- •2. Последовательный симплексный метод поиска экстремума функций
- •Оценка регрессии
- •Градиентный метод с использованием планирования первого порядка
- •Один из простых вариантов алгоритма Ньютона имеет вид
№1
1)Общая схема проверки гипотез
вероятности ошибочных решений
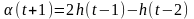 ,
,

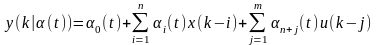 – вероятность
правильного решения
– вероятность
правильного решения
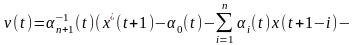 – вероятность
ошибочного решения
– вероятность
ошибочного решения
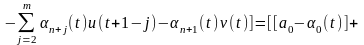 и
и
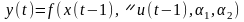 - пороги
- пороги
2) Постановка задачи адаптивного управления
Считаем, что поведение объекта в динамическом режиме описывается разностным уравнением
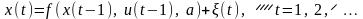
Если
шум
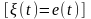 белый, то
белый, то
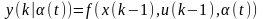 .
.
прогноз
выхода следующего момента времени:
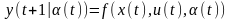
№2
1)Проверка гипотезы о математическом ожидании
Вводим
статистику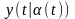 ,где
,где
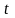 .
.
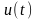
а)
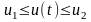 .
Левый
.
Левый
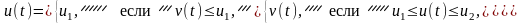 и правый
и правый
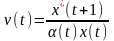 пороги (в алгоритме проверки гипотез)
зависят только от одной константы
пороги (в алгоритме проверки гипотез)
зависят только от одной константы
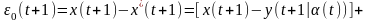 .
Этот случай отражен на рис. 1.2.1. Гипотеза
.
Этот случай отражен на рис. 1.2.1. Гипотеза
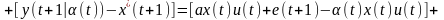 верна, если величина
верна, если величина
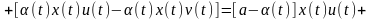 .
Порог
.
Порог
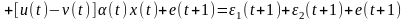 находим из условия
находим из условия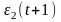
2)
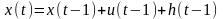
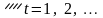
Формируем
модель объекта
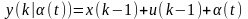 .
.
Вычислим
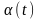 приравняв выход модели
и выход объекта
приравняв выход модели
и выход объекта
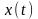 в момент времени
:
в момент времени
:
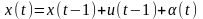 .
получаем параметр
.
получаем параметр
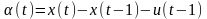 .
.
рассчитываем оптимальное управление:
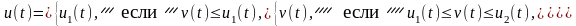
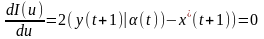
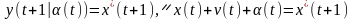
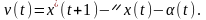
№3
Проверка гипотезы о равенстве дисперсий
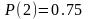
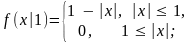 о том, что
о том, что
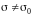 .Вводим
статистику (хи-квадрат):
.Вводим
статистику (хи-квадрат):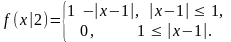 ,
где
,
где
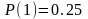 .находим
пороговые значения
.находим
пороговые значения
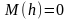 и
и
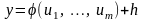 ,
соответствующие условиям:
,
соответствующие условиям: ,
,
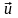
2) синтез алгоритмов управления для линейной модели
Параметры модели
рассчитываем по одному из адаптивных алгоритмов (см. гл. 6, 7). Оптимальное управление находим из критерия
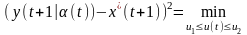
и получаем его в виде идеальное управление
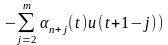
№4
1) Проверки гипотезы о равенстве мат.ожиданий
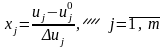 о
том, что
о
том, что
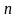 ,
и конкурирующая гипотеза (
,
и конкурирующая гипотеза (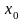 )
о том, что
)
о том, что
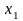 .
Эти гипотезы проверяются по статистике
.
Эти гипотезы проверяются по статистике
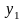 ,где
,где
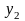 ,
,
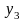 .
.
При
истинности
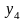 случайная величина
распределена по нормальному закону
случайная величина
распределена по нормальному закону
 .
Порог
находится из табл. П1 (см. задачу 1):
.
Порог
находится из табл. П1 (см. задачу 1):
 .
Условия
принятия гипотез
.
Условия
принятия гипотез
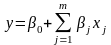 ,
,
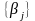 таковы:
таковы:
если
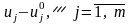 ,
то принимаем
,
то принимаем
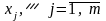 ;
если
;
если
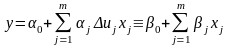 или
,
то отвергаем
или
,
то отвергаем
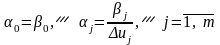 .
.
№5
Выявление аномальных измерений
Строим
статистику:
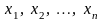 .
Теперь рассмотрим ситуацию, когда
дисперсия
.
Теперь рассмотрим ситуацию, когда
дисперсия
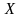 неизвестна. Статистика имеет вид
неизвестна. Статистика имеет вид
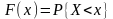 .
При истинности гипотезы
.
При истинности гипотезы
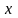 случайная величина
распределяется по закону Стьюдента
случайная величина
распределяется по закону Стьюдента
№6
Гипотеза об однородности ряда дисперсий имеем несколько случайных величин
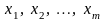 ,
распределенных по нормальному закону
,
... ,
,
распределенных по нормальному закону
,
... ,
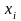 .
Все параметры
,
.
Все параметры
,
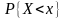 неизвестны. Для каждой случайной
величины производятся независимые
измерения одинакового объема
неизвестны. Для каждой случайной
величины производятся независимые
измерения одинакового объема
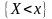 и проверяется гипотеза о равенстве
дисперсий:
и проверяется гипотеза о равенстве
дисперсий:
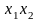 .
Строим статистику по методу Кочрена
(W.
G.
Cochran),
так как для всех случайных величин
имеем одинаковое число повторных опытов
.
Строим статистику по методу Кочрена
(W.
G.
Cochran),
так как для всех случайных величин
имеем одинаковое число повторных опытов
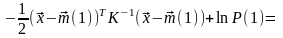 .
.
Статистика
имеет вид: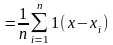 ,
где
,
где
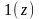 .
.
№7
Гипотеза о распределениях
вероятность
попадания случайной величины
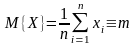 в
-й
интервал
в
-й
интервал
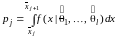 .
.
Проверка
этой гипотезы базируется на статистике,
построенной на уклонениях
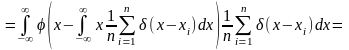 и
и
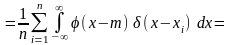 :
:
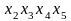 .
.
№8
Байесовская теория принятия решений при дискретных признаках
1. Одномерный вариант
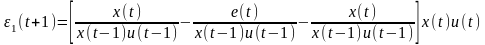
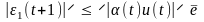 .
.
Выносим решение об истинности того класса (с номером ), для которого апостериорная вероятность максимальная:
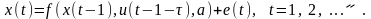 .
.
2. Многомерный вариант
Имеется
несколько дискретных информативных
признаков
.
Для простоты считаем, что имеются два
информативных признака
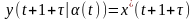 .
.
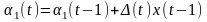 ,
,
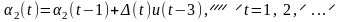 .
.
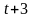 ,
,
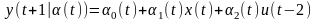 .
.
Известны
также априорные вероятности классов
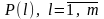 .
.
По формуле Байеса вычисляем апостериорные вероятности для всех рассматриваемых классов:
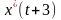 .
.
2) Структуры дискретных динамических моделей стохастических объектов
объект описывается дискретным уравнением
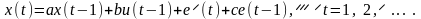
Здесь
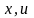 – измеряемые скалярные выход и вход
объекта;
– измеряемые скалярные выход и вход
объекта;
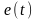 – некоррелированная во времени
центрированная помеха (белый шум);
– некоррелированная во времени
центрированная помеха (белый шум);
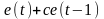 =
=
=
=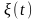 – коррелированная (окрашенная) помеха;
– коррелированная (окрашенная) помеха;
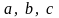 – неизвестные параметры. Обозначим
через
– неизвестные параметры. Обозначим
через
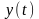 выход модели в момент времени
.оптимальная
(в смысле минимума среднего квадратического
значения невязки
выход модели в момент времени
.оптимальная
(в смысле минимума среднего квадратического
значения невязки
 :
:
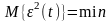 )
модель имеет вид
)
модель имеет вид
 .
.
№9
