
- •Функции и способы их задания. Элементарные функции
- •Предел последовательности. Сходящиеся и расходящиеся последовательности.
- •Определение предела функции. Примеры.
- •Основные свойства пределов. Замечательные пределы.
- •Непрерывность функции. Точки разрыва 1 и 2 рода.
- •Свойства непрерывных функций
- •Производная функции. Геометрический и физический смысл производной.
- •Дифференциал функции. Основные правила дифференцирования.
- •9) Основные правила дифференциального исчисления.
- •10 ) Правило Лопиталя. Формулы Тейлора и Маклорена.
- •11) Исследование функции с помощью дифференциального исчисления.
- •12) Функции нескольких переменных. Частные производные.
- •13) Условный экстремум. Метод множителей Лагранжа.
- •14) Неопределенный интеграл и его основные свойства.
- •15) Замена переменных и интегрирование по частям для неопределенного интеграла.
- •16) Интегрирование рациональных функций.
- •17) (Подписать к графику!!) Интегральная сумма и определенный интеграл.
- •18) Основные свойства определенных интегралов. Методы интегрирования.
- •19) Геометрические приложения определенного интеграла.
- •1) Вычисление площади плоских фигур
- •2) Вычисление объема
- •20) Приближенное вычисление определенного интеграла. Методы интегрирования.
- •1) Формула прямоугольников
- •2) Формула трапеции
- •21) Дифференциальные уравнения. Примеры задач, приводящих к дифференциальным уравнениям.
- •22) Задача Коши и теорема Коши.
- •23) Дифференциальные уравнения с разделяющимися переменными.
- •24) Решение дифференциальных уравнений методом подстановки (метод Бернулли)
- •Первый способ
- •Второй способ
- •25) Решение дифференциальных уравнений методом вариации постоянной (метод Лангранжа) Метод вариации постоянной (метод Лагранжа)
21) Дифференциальные уравнения. Примеры задач, приводящих к дифференциальным уравнениям.
Порядок дифференциального уравнения. Общее и частное решение. 1) Определение
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную х, неизвестную функцию y=y(x) и её производные y’,y”,…
F(x,y,y’,y”,
… ,
 )=0
(n
обозначает n-ую
производную)
)=0
(n
обозначает n-ую
производную)
Примеры задач, приводящих к дифференциальным уравнениям.
1) Измерение стоимости оборудования
Пусть S(t)-стоимость оборудования в момент времени t. Известно, что ст-ть оборудования снижается со временем за счёт износа. Скорость обесценивания в любой момент времени пропорциональна фактической ст-ти в данный момент. Поэтому S(t) удовлетворяет уравнению: S’(t)=-kS(t) , где k>0 – константа
Ст-ть падает, поэтому производная S’ отрицательна знак справа – минус.
2) Свободное падение
Камень бросают с башни высоты h0=50м. Как меняется расстояние до земли со временем?
Пусть
h=h(t)
– высота, на которой камень находится
через t
секунд после начала падения. Известно,
что ускорение, т.е. h”
– постоянная величина, равна 9,8м/ .
Поэтому h”(t)=-g
.
Поэтому h”(t)=-g
3) Известно, что скорость размножения бактерий положительна и пропорциональна их общему кол-ву, т.е. массе. Пусть m=m(t) – масса в момент времени t. Тогда dm/dt=km(t), k>0
4) тело, имеющее в начальный момент времени t=0 температуру Т0=100˚ охлаждается в воздушной среде до температуры Т1=60˚ за время t1=20минут. Температура воздуха равна 20˚. Скорость охлаждения пропорциональна разности между температурой тела и температурой охлаждающей среды. За какое время тело охладится до температуры 30˚?
Пусть Т=Т(t) – температура в момент времени t. Тогда dT/dt=k(T-20). Т(0)=100.
Необходимо найти t2, при котором Т(t2)=30/
Решение.
 =k.
Обозначим Т-20=Х
y’/y=k,
т.е. (lny)’=k.
Поэтому lny=kt+b,
и y=
=k.
Обозначим Т-20=Х
y’/y=k,
т.е. (lny)’=k.
Поэтому lny=kt+b,
и y=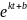 =
= =c
=c ,
где с-константа(с>0)
,
где с-константа(с>0)
1)
При t=0
y=T-20=C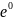 =c.
Так как Т=100˚
100-20=C,
С=80
=c.
Так как Т=100˚
100-20=C,
С=80
2)
При t=20
T=60˚60=80
 =
= и Т=80
+20=80*
и Т=80
+20=80*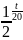 +20
+20
3)
при t=t2
должно быть 30=80* +20,
поэтому
+20,
поэтому
 =3
и t2=60.
=3
и t2=60.
Следовательно тело охладиться до температуры 30˚ через 60 минут.
Порядок дифференциального уравнения.
Порядком дифф уравнения называется наибольший порядок производных, входящих в данное уравнение.
Определение.
Функция y=f(x) называется (частным) решением уравнения, если при подстановке её в уравнение оно становится тождеством.
Определение.
Функция y=y(x,c1, … , cn) от одной переменной х, зависящая от n независимых параметров c1, …, cn называется общим уравнением F(x,y,y’,y”, … , )=0 n-го порядка, если при любых конкретных значениях параметра с1, …, cn она является его частным решением.
Начальные
условия. Если
ищется решение дифф уравнения F(x,y,y’,y”,
… ,
)=0
в области х≥х0, то значения y0=y(x0),
y’0=y’(x0),
… ,
 =
= называют начальным условием.
называют начальным условием.
Общее и частное решение уравнения.
Определение
Общим
решением уравнения y’=f(x,y)
в некоторой области G
плоскости Oxy
называется функция y=φ(x,C)
, зависящая от х и произвольной постоянной
С, если она является решением уравнения
при любом значении постоянной С, и если
при любых начальных условиях таких, что
(х0,y0) G,
существует единственное значение
постоянной С=С0 такое, что функция
y=φ(x,C0)
удовлетворяет данным начальным условиям
φ(x0,C)=y0.
G,
существует единственное значение
постоянной С=С0 такое, что функция
y=φ(x,C0)
удовлетворяет данным начальным условиям
φ(x0,C)=y0.
Определение
Частным решением уравнения y’=f(x,y) в области G называется функция y=φ(x,C0), которая получается из общего решения y=φ(x,C) при определенном значении постоянной С=С0
