
- •Функции и способы их задания. Элементарные функции
- •Предел последовательности. Сходящиеся и расходящиеся последовательности.
- •Определение предела функции. Примеры.
- •Основные свойства пределов. Замечательные пределы.
- •Непрерывность функции. Точки разрыва 1 и 2 рода.
- •Свойства непрерывных функций
- •Производная функции. Геометрический и физический смысл производной.
- •Дифференциал функции. Основные правила дифференцирования.
- •9) Основные правила дифференциального исчисления.
- •10 ) Правило Лопиталя. Формулы Тейлора и Маклорена.
- •11) Исследование функции с помощью дифференциального исчисления.
- •12) Функции нескольких переменных. Частные производные.
- •13) Условный экстремум. Метод множителей Лагранжа.
- •14) Неопределенный интеграл и его основные свойства.
- •15) Замена переменных и интегрирование по частям для неопределенного интеграла.
- •16) Интегрирование рациональных функций.
- •17) (Подписать к графику!!) Интегральная сумма и определенный интеграл.
- •18) Основные свойства определенных интегралов. Методы интегрирования.
- •19) Геометрические приложения определенного интеграла.
- •1) Вычисление площади плоских фигур
- •2) Вычисление объема
- •20) Приближенное вычисление определенного интеграла. Методы интегрирования.
- •1) Формула прямоугольников
- •2) Формула трапеции
- •21) Дифференциальные уравнения. Примеры задач, приводящих к дифференциальным уравнениям.
- •22) Задача Коши и теорема Коши.
- •23) Дифференциальные уравнения с разделяющимися переменными.
- •24) Решение дифференциальных уравнений методом подстановки (метод Бернулли)
- •Первый способ
- •Второй способ
- •25) Решение дифференциальных уравнений методом вариации постоянной (метод Лангранжа) Метод вариации постоянной (метод Лагранжа)
9) Основные правила дифференциального исчисления.
1) Теорема Ролля.
Пусть f(x) непрерывна на отрезке и дифференцируема в каждой внутренней точке. Пусть f(a)=f(b). Тогда на существует хотя бы 1 точка С, такая, что f’(c)=0.
Пример:
f(x)=sin x, a=0, b=П. f(0)= sin0=0.
f(П)=sin П=0.
f(x)= cos x =0⇒
x=
2 ) Теорема Лагранжа.
Пусть
f(x)
непрерывна на отрезке
и дифференцируема в каждой внутренней
точке. Тогда существует С принадлежащая
,
f’(c) =
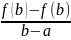
Пример:
f(x)
= x2,
a=0, b=1.
=
 = 4= f’(c) = 2c⇒
c=2
= 4= f’(c) = 2c⇒
c=2
Теорема Ферма.
Пусть f(x) непрерывна на отрезке и дифференцируема. Пусть в некоторой точке С функция принимает макс. и миним. значение. Тогда f’(c)=0.
10 ) Правило Лопиталя. Формулы Тейлора и Маклорена.
Правило Лопиталя.
Теорема: Пусть f(x) и g(x) определены в некоторой окружности точки а (кроме, быть может, самой точки а). Тогда если в точке а существует предел отношения самих функций и эти пределы равны.
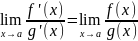
Примеры:
 =
=
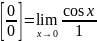 (если при подстановке вместо х 0 (или
∞) получается неопределенность вида
(если при подстановке вместо х 0 (или
∞) получается неопределенность вида
 (или
(или
 ),
то мы используем правило Лопиталя:
находим производную от числителя и
знаменателя и подставляем значение х
уже в производную)
),
то мы используем правило Лопиталя:
находим производную от числителя и
знаменателя и подставляем значение х
уже в производную)
Формулы Тейлора и Маклорена. f(n+1)
Пусть
функция f(x)
имеет в точке а и её окрестности
производных до n-порядка.
Если x-любое число из
указанной окрестности, x≠a,
то
f(x)
= f(a)
+
 (x-a)
+
(x-a)
+
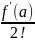 (x-a)2
+ … +
(x-a)2
+ … +
 (x-a)n
+ Rn+1(x)
ф-ла Тейлора.
(x-a)n
+ Rn+1(x)
ф-ла Тейлора.
Rn+1(x)-остаточный член, характеризующий погрешность формулы.
Rn+1(x)=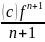 (x-a)n+1,
c-некоторое
число, такое, что a<
c
< x
формула
Маклорена
(x-a)n+1,
c-некоторое
число, такое, что a<
c
< x
формула
Маклорена
11) Исследование функции с помощью дифференциального исчисления.
1) Промежутки возрастания и убывания функции.
Если на (a;b) f’(x)˃0, то f(x) возрастает. Если на (a;b) f’(x)<0, то f(x) убывает.
2 ) Точки локального экстремума.
Точка а – точка локального экстремума функции f(x), если в некоторой окрестности точки а все значения функции строго меньше f(a). Точка локального экстремума - это точки максимума или минимума.
3 ) Достаточное условие локального max и min
Локальный min:
-
X < С
X=C
X ˃ C
f’(x) < 0
f’(x)=0
f’(x) ˃ 0
Локальный max:
-
X < C
X=C
X ˃ C
f’(x) ˃ 0
f’(x)= 0
F’(x) < 0
Т
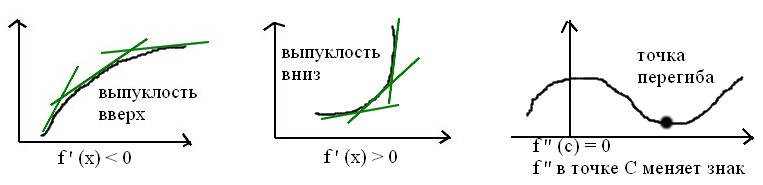 очки
перегиба и выпуклость графика функции.
очки
перегиба и выпуклость графика функции.
Асимптоты графика функции.
Асимптотой называется прямая, к которой сколь угодно близко приближается график функции f(x) при х а или при х∞
В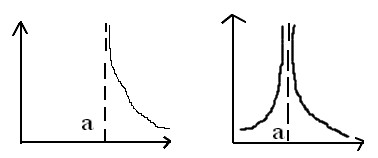 ертикальная
асимптота.
ертикальная
асимптота.
Прямая х=а – вертикальная асимптота.
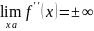
Г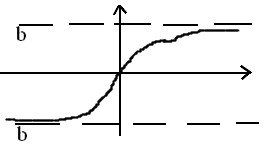 оризонтальная
асимптота:
оризонтальная
асимптота:
Прямая у = b – горизонтальная асимптота.
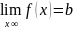 ,
,

Н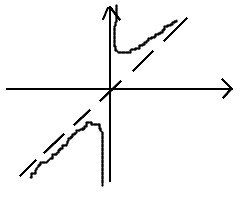 аклонная
асимптота:
аклонная
асимптота:
Прямая
y=
kx
+ b
– накл. асимптота, если
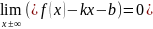
Схема исследования функции:
Область определения
Четность, нечетность, периодичность
Точки пересечения графика с осями координат
Точки разрыва
Точки экстремума, промежутки возрастания и убывания
Точки перегиба, выпуклости
Асимптоты
Построение графика
