40. Понятие случайной величины (св). Виды св.

Величина называется случайной, если она принимает свои значения в зависимости от исходов некоторого испытания (опыта), причем для каждого элементарного исхода она имеет единственное значение.

СВ, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной (ДСВ).

Геометрически множество всех возможных значений дискретной случайной величины представляет конечную систему точек числовой оси.

СВ, которая принимает все значения из некоторого промежутка – непрерывная случайная величина (НСВ).

41. Закон распределения дискретной св. Ряд распределения. Многоугольник распределения.

Пусть X — дискретная случайная величина, возможными и единственно возможными значениями которой являются числа x₁, х₂, …, х_n.

Обозначим через

p_i = Р(Х=х_i) (i = 1, 2…n)

вероятности этих значений (т. е. p_i есть вероятность события, состоящего в том, что X принимает значение x_i).

События X = x_i (i = 1, 2, …, n), очевидно, образуют полную группу событий, поэтому

p₁+p₂+…+p_n=1

Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.

Закон распределения может быть задан таблично, графически и аналитически. При табличном задании 1 строка – значения величина, 2 строка – вероятности.

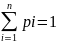
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Для наглядности закон распределения ДСВ изображают графически: в системе координат строят точки (x_i; p_i) и соединяют их отрезками. Полученная ломаная называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

42. Понятие математического ожидания дискретной св, его свойства

Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.

            Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

            Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно.

            С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства:

 1°. Математическое ожидание постоянной С равно этой постоянной. 2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

 3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин.