7. Деформация изгиба

В инженерной практике рассчитывать на изгиб элементы конструкций приходится чаще всего. Эти элементы обычно называют балками. Мы тоже будем использовать этот термин. Рассмотрим изгиб балки, шарнирно закрепленной на двух опорах, рис.1.16.

В идим, что при изгибе верхние волокна балки сжались, а нижние растянулись. Следовательно, основными напряжениями в сечениях балки будут нормальные напряжения σ. В произвольном сечении I - I в общем случае могут возникнуть 3 внутренних усилия: N; Q; Мизг.

Рис.1.16 Однако, в условии прочности учитывается только Мизг. Это не значит, что мы не должны уметь определять N и Q, особенно поперечную силу Q, поскольку в основном она определяет нагрузки в узловых точках балки.

Запишем условие прочности.

σ = Мизг /W ≤ [σ] (1.13)

- условие прочности при изгибе

Здесь W – момент сопротивления сечения изгибу (см. геометрические характеристики сечений).

На рис.1.16 показана эпюра напряжений по высоте сечения. Видим, что максимальные напряжения находятся на периферии сечения, при этом отрицательные напряжения в сжатых волокнах постепенно переходят в положительные напряжения в растянутых волокнах. В средних сечениях балки проходит нейтральный слой (σ = 0). Следовательно, при изгибе балки ее середина (по высоте сечений) не работает. Учитывая этот факт, для уменьшения веса конструкции, необходимо подбирать такие сечения, у которых основной материал расположен на периферии, а в середине он минимален.

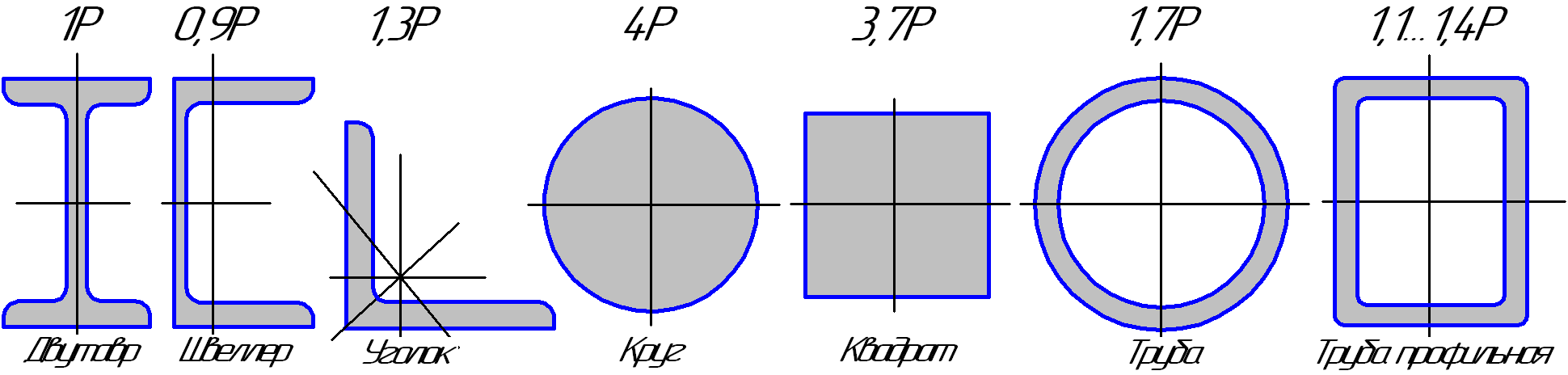
Рис.1.17

На рис.1.17 показано несколько стандартных профилей и дано соотношение их весов при одинаковых значениях W. За 1Р принят вес двутавра.

А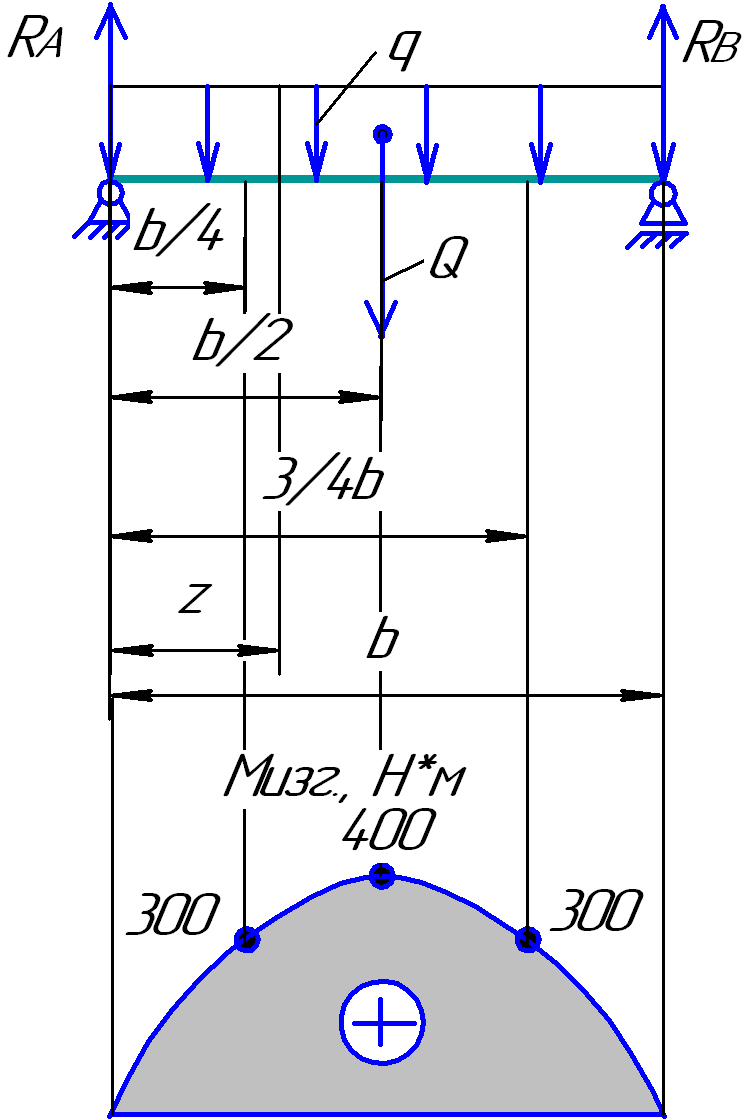 нализируя данные, приведенные на рис.1.17, видим, что при одинаковой прочности наиболее легкой будет конструкция, выполненная из швеллера. Например, конструкция из швеллера весит 100 кг, аналогичная конструкция, выполненная из круга, будет весить 444 кг. А это деньги и не малые, учитывая стоимость металла. Кроме того, такая конструкция из-за больших моссо-габаритных параметров будет не конкурентно способной.

Рассмотрим несколько примеров расчета балок на изгиб. В первую очередь вернемся к рис.1.7. Нужно рассчитать опорные элементы под настил стелажа. Расчетная схема показана на рис.1.18.

Дано:

q = 5000 Н/м; в = 0,8 м; σ_в = 370 МПа; n = 5;

[σ] = σ_в/n = 370/5 = 74 МПа.

Требуется:

подобрать прямоугольную тонкостенную трубу.

Решение.

Определим реакции опор.

Рис.1.18

∑M_В = 0. R_А*b – Q*b/2 = 0.

Здесь Q = q*b – результирующая распределенной нагрузки. R_А = Q*b/2b = Q/2 = 5000*0,8/2 = 2000 Н. Нагрузка симметрична относительно опор, поэтому R_В = R_А = 2000 Н.

Проверка.

∑F_y = 0. R_А + R_В – Q = 0. 2000 + 2000 – 5000*0,8 = 0.

Реакции найдены правильно.

Построим эпюру моментов изгибающих.

М(z) = R_А*z – q*z*z/2. Здесь z – текущая координата.

Поскольку зависимость момента от z квадратичная, необходимо длину балки разбить на несколько участков, найти моменты на границах участков и построить эпюру.

z = 0. М(0) = 0.

z = b/4. М(b/4) = R_А* b/4 - q* b²/32 = 2000*0,8/4 – 5000*0,8²/32 = 300 Н*м.

z = b/2. М(b/2) = R_А* b/2 - q* b²/8 = 2000*0,8/2 – 5000*0,8²/8 = 400 Н*м.

z =3/4b. М(3/4b)= R_А* 3/4b - q*9b²/32 = 2000*3*0,8/4 – 5000*9*0,8²/32 = 300 Н*м.

z = b. М(b) = R_А* b - q* b²/2 = 2000*0,8 – 5000*0,8²/2 = 0.

П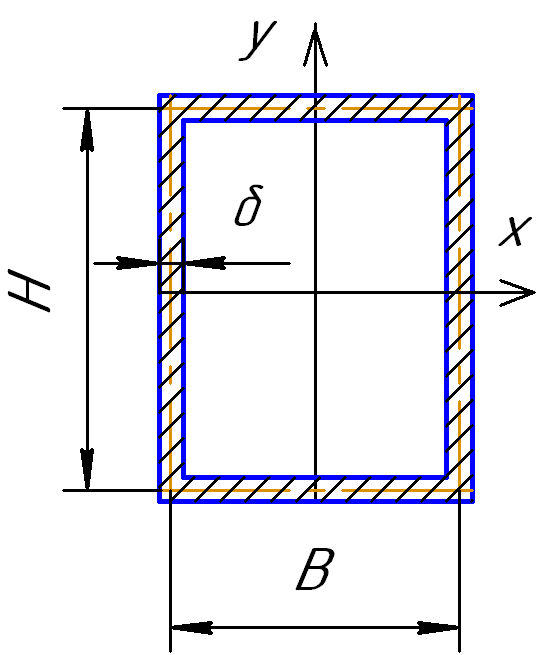 о полученным данным построили эпюру Мизг. (рис.1.18).

Из условия прочности σ = Мизг /W ≤ [σ] выразим W.

W ≥ Мизг/[σ] = 400*10³/74 = 5405 мм³.

Для тонкостенной прямоугольной трубы (рис.1.19) Wх определяется по формуле.

Wх = δ*Н²*(3В/Н + 1)/3.

Предположим, что мы хотим использовать трубу, один из наружных размеров которой равен 40мм. Имеются трубы: 1) 40х40х2; 2) 40х40х2,5; 3) 40х40х3; 4) 40х60х2;

Рис.1.19 5) 40х60х2,5; 6) 40х60х3.

Нам желательна труба с наименьшим весом.

Находим Wх для каждой из труб.

Wх₁ = 2*38²*4/3 = 2888 мм³ < 5405 мм³ – не подходит.

Wх₂ = 2,5*37,5²*4/3 = 4688 мм³ < 5405 мм³ – не подходит.

Рис.1.19 Wх₃ = 3*37²*4/3 = 5476 мм³ > 5405 мм³ – подходит.

Wх₄ = 2*58²*(3*38/58 + 1)/3 = 6650 мм³ > 5405 мм³ – подходит.

Сравниваем две трубы по весу. Их веса пропорциональны площадям сечений.

А₃ = 4Н* δ = 4*37*3 = 444 мм².

А₄ = (2Н + 2В)* δ = (2*58 + 2*38)*2 = 384 мм².

Следовательно труба 40х60х2 легче трубы 40х40х3,

больше того она прочнее в 6650/5476 = 1,2 раза.

Выбор ясен – принимаем трубу 40х60х2.

Решим более сложную задачу.

Необходимо подобрать швеллер для элемента рамы, на который действуют: распределенная нагрузка, изгибающий момент и сосредоточенная сила. Расчетная схема показана на рис.1.20.

Дано:

F = 20 кН; М = 5 кН*м; q = 20 кН/м;

материал Сталь 20, имеющая σ_в = 412 МПа;

a = 2 м; b = 1 м; c = 1 м; d = 1 м; l = 5 м.

Условия работы конструкции не высокой опасности. Достаточно принять коэффициент запаса прочности n = 3.

Соответственно [σ] = σ_в/ n = 412/3 = 137 МПа.

Требуется:

1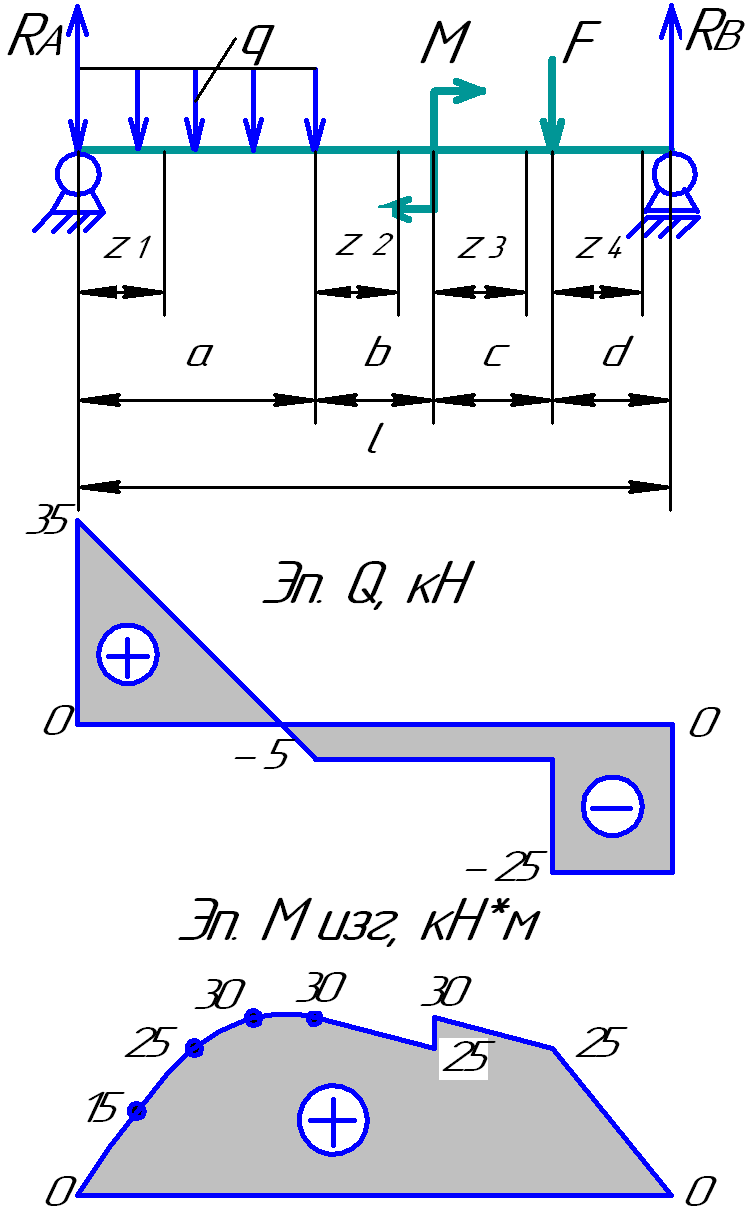 – построить эпюры поперечных сил и изгибающих моментов;

2 – подобрать необходимый швеллер.

Решение.

Запишем условие прочности

σ = Мизг /W ≤ [σ]. Выразим W.

W ≥ Мизг/[σ].

Необходимо найти максимальный Мизг.

Определим реакции опор.

∑M_В = 0.

R_А*l – Q*(a/2 + b + c +d) + M – F*d = 0.

Здесь Q = q* a = 20*2 = 40 кН.

R_А = [Q*(a/2 + b + c +d) - M + F*d]/l =

= [40*(1 + 1 + 1 + 1) – 5 + 20*1]/5 = 35 кН.

∑M_А = 0.

R_В*l – F*( a + b + c) - M - Q*a/2 = 0.

R_В = [F*( a + b + c) + M + Q*a/2]/l =

Рис.1.20 = (20*4 + 5 + 40*1)/5 = 25 кН.

Проверка.

∑F_Y = 0. R_А + R_В – Q – F = 35 + 25 – 40 – 20 = 0.

Построим эпюру поперечных сил.

Q(z₁) = R_А – q* z₁. 0 ≤ z₁ ≤ a.

Q(0) = R_А = 35 кН. Q(а) = R_А – q*а = 35 – 20*2 = - 5 кН.

Q(z₂) = Q(z₃) = R_А – Q = 35 – 40 = - 5 кН.

Q(z₄) = R_А – Q – F = 35 – 40 - 20 = - 25 кН. 0 ≤ z₄ ≤ d.

При z₄ = d, Q(d) = R_А – Q – F + R_В = 35 – 40 –20 +25 = 0.

Таким образом система уравновесилась – с 0 началась и 0-м закончилась.

Построим эпюру моментов изгибающих.

М(z₁) = R_А* z₁ - q* z₁²/2. 0 ≤ z₁ ≤ a. Зависимость М от z₁ не линейная, поэтому, как и в предыдущей задаче, разобьем отрезок а на 4 участка и найдем моменты на границах участков.

М(0) = 0.

М(а/4) = R_А* а/4 - q* а²/32 = 35*0,5 – 20*0,125 = 15 кН*м.

М(а/2) = R_А* а/2 - q* а²/8 = 35*1 – 20*0,5 = 25 кН*м.

М(3/4а) = R_А* 3/4а - q* а²*9/32 = 35*1,5 – 20*1,125 = 30 кН*м.

М(а) = R_А* а - q* а²/2 = 35*2 – 20*2 = 30 кН*м.

М(z₂) = R_А* (а + z₂) – Q*(а/2 + z₂). 0 ≤ z₂ ≤ b.

М(0) = R_А*а – Q*а/2 = 35*2 – 40*1 = 30 кН*м.

М(b) = R_А* (а + b) – Q*(а/2 + b) = 35* 3 – 40*2 = 25 кН*м.

М(z₃) = R_А* (а + b + z₃) – Q*(а/2 + b + z₃) + М. 0 ≤ z₃ ≤ с.

М(0) = R_А*(а + b) – Q*(а/2 + b) + М = 35* 3 – 40*2 + 5 = 30 кН*м.

М(с) = R_А* (а + b + с) – Q*(а/2 + b + с) + М = 35*4 – 40* 3 + 5 = 25 кН*м.

М(z₃) = R_А* (а + b + с + z₄) – Q*(а/2 + b + с + z₄) + М – F* z_4. 0 ≤ z₄ ≤ d.

М(0) = R_А* (а + b + с) – Q*(а/2 + b + с) + М = 35*4 – 40* 3 + 5 = 25 кН*м.

М(d) = R_А* (а + b + с + d) – Q*(а/2 + b + с + d) + М – F* d =

35*5 – 40*4 + 5 – 20*1 = 0.

По полученным данным построена эпюра моментов изгибающих. Максимальный изгибающий момент равен М = 30 кН*м.

Определим Wх.

Wх ≥ Мизг/[σ] = 30*10⁶/ 137 = 219*10³ мм³ = 219 см³.

Сомножитель 10⁶ появился при переводе кН в Н и м в мм.

В справочной литературе Wх дается в см³.

Нам нужен швеллер, у которого Wх ≥ 219 см³.

Ближайший швеллер, который нам подходит, № 24, у него Wх = 242 см³.

Рассмотренная нами методика прочностных расчетов на изгиб позволит Вам решать большинство Ваших реальных инженерных задач. Рекомендую Вам попрактиковаться, решив несколько задач из рекомендованной литературы или из Вашей практической деятельности.