4. Фрикционные передачи

Во фрикционных передачах движение от ведущего звена к ведомому передается за счет сил трения, возникающих между прижатыми друг к другу колесами. Различают передачи с постоянным передаточным отношением и с переменным передаточным отношением. Последние называются фрикционные вариаторы.

Н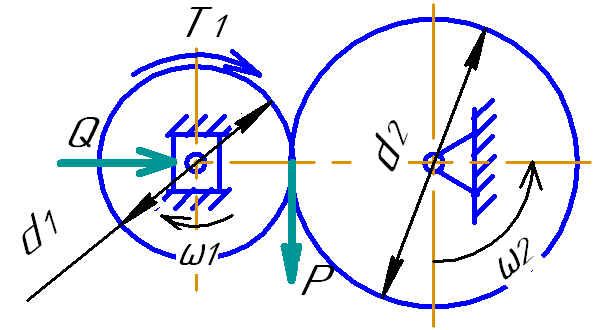 а рис.4.14 показана схема фрикционной передачи с постоянным передаточным отношением.

По этому рисунку составим основы теории фрикционных передач, отметим из достоинства и недостатки.

Ведущий каток передает крутящий момент

Рис. 4.14 Т₁ = Р*d₁/2. В месте касания катков возникает сила трения F = Q*f, где f – коэффициент трения скольжения.

Для предотвращения проскальзывания катков необходим некоторый запас надежности сцепления.

k = F/P = Q* f* d₁/ 2Т₁ > 1, откуда необходимое условие прижатия катков

Q = 2 k* Т₁/( f* d₁) = k*P/f (4.31)

k – коэффициент надежности сцепления.

Для силовых передач принимают k = 1,25…1,5; в приборах k = 3 и более.

Для пары сталь – сталь f = 0,05 при работе со смазкой; f = 0,1…0,15 при работе всухую.

Предположим, что необходима сила Р = 100 Н. Приняли f = 0,12; k = 1,3. Тогда Q = k*P/f = 1,3*100/0,12 = 1083 Н. То есть чтобы получить силу всего 100Н необходимо прижимать катки силой 1083 Н. Это существенный недостаток фрикционных передач с линейным или точечным контактом звеньев. К достоинствам фрикционных передач можно отнести: простоту конструкций; плавность и бесшумность работы; предохранение от поломок при перегрузках (будет происходить проскальзывание).

Расчет элементов передачи проводят, как правило, на контактную прочность по формуле Герца (4.4), аналогично расчету зубчатых колес. Поэтому здесь мы не будем останавливаться на этом вопросе.

Передаточное отношение.

u_1-2 = ω₁/ω₂ = d₂/[d₁*(1 – ξ)], (4.32)

где ξ = 0,002…0,05 – коэффициент, учитывающий проскальзывание в передаче (определяется экспериментально). Довольно широкий диапазон значений говорит о том, что этот коэффициент приблизительный и может меняться в процессе эксплуатации передачи.

Фрикционные вариаторы

На рис. 4.15 приведены три схемы вариаторов. Лобовой вариатор (рис. 4.15, а). В нем при постоянном R₁ меняется R₂, поэтому u = R₂/ R₁ # const. Вариатор с конусными барабанами и промежуточным роликом (рис. 4.15, б), который перемещается вдоль своей оси. При этом R₁ и R₂ изменяются. Соответственно u = R₂/ R₁ # const.

Н а рис. 4.15, в) показан клиноременной вариатор с подвижными конусами. Перемещение конусов ведомого звена осуществляется с помощью винтового механизма. Постоянную натяжку ремня выполняет пружина, установленная на ведущем звене. При этом R₁ и R₂ изменяются.

u = R₂/ R₁ # const.

Все показанные вариаторы могут работать как в режиме понижения оборотов (редуктор) при R₂ > R₁ , так и в режиме повышения оборотов

(мультипликатор) при R₂ < R₁.

Рис.4.15 Вариаторы по схемам (рис. 4.15, а; б) не могут передавать большие крутящие моменты, поэтому применяются в основном в приборах и других маломощных механизмах. Клиноременной вариатор, имея достоинства обычной клиноременной передачи и способный плавно регулировать скорость на ведомом валу, применяется в силовых механизмах и машинах. В частности, на снегоходе «Буран» вместо коробки передач установлен клиноременной вариатор.