Червячные передачи
Ч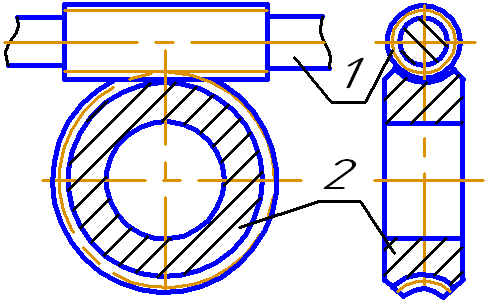
ервячные
передачи (рис. 4.12) относятся к числу
зубчато-винтовых, имеющих характерные
черты зубчатых и винтовых передач. Они
состоят из червяка 1 и червячного колеса
2. Червяк представляет собой винт с
резьбой близкой к трапецеидальной.
Червячное колесо – это косозубое
цилиндрическое колесо, особенностью
которого является огибание
зубьями колеса части
Рис. 4.12 окружности червяка. У червяка нет зубьев, у него есть винтовые нарезки (винтовые линии). Количество винтовых линий (при взгляде с торца червяка) называется числом заходов червяка z1. В червячных редукторах обычно z1 = 1 или 2.
Передаточное отношение равно u = z2/ z1, где z2 – число зубьев червячного колеса.
Основные достоинства червячных передач: большое передаточное число при малых габаритах передачи (в стандартных редукторах u = 8…100); возможность самоторможения (используется в грузоподъемных механизмах); плавность и бесшумность работы.
Н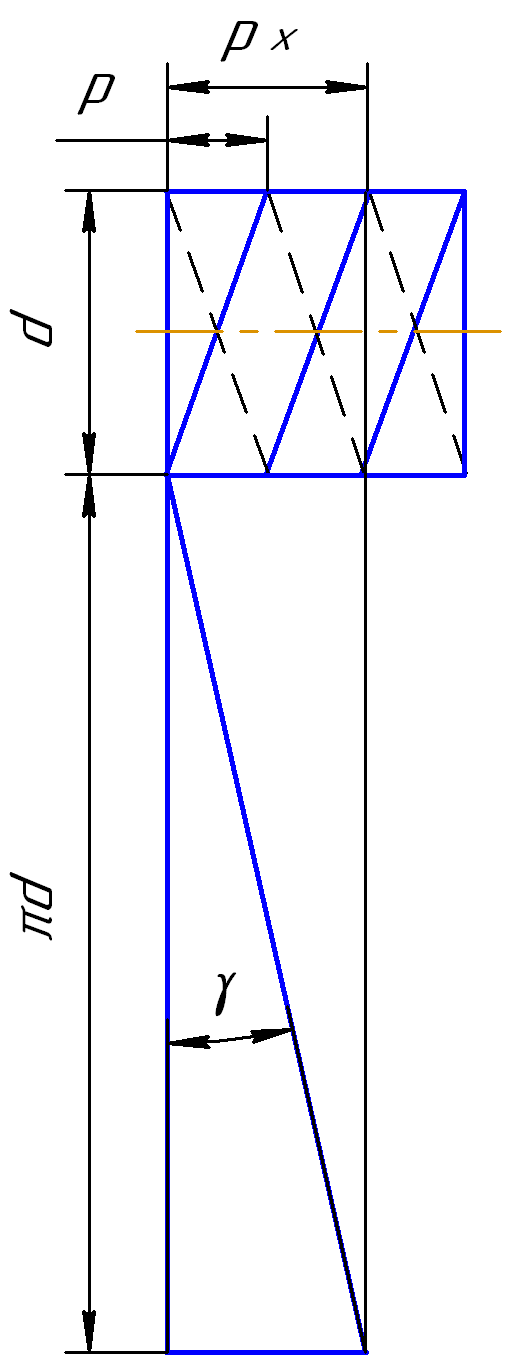
едостатки:
низкий КПД (0,7…0,85); необходимость
применения для колеса дорогостоящих
антифрикционных материалов.
Материалы червячных передач: червяк стальной закаленный и желательно шлифованный; червячное колесо или его венец – бронзовые, в крупногабаритных передачах – чугунные.
На рис. 4.13 показана развертка винтовой линии двухзаходного червяка по делительной окружности. На рисунке приняты обозначения: p – шаг червяка (p = π*m); px – ход винтовой линии; d – делительный диаметр червяка; γ – делительный угол подъема витка червяка.
Очевидно соотношение px = p* z1 = π* m* z1
Видим px/ (πd) = tq γ, отсюда , заменяя px = π* m* z1, получаем
d = m* z1/ tq γ = q* m .
Параметр q = z1/tq γ (4.23)
называется коэффициентом диаметра червяка. Эта
Рис. 4.13 величина стандартизована.
ГОСТ 2144-76 рекомендует ряд значений q в сочетании с рядом модулей.
Остальные параметры (элементы) передачи определяются аналогично зубчатым передачам.
da1 = d1 + 2m = m*( q +2); df1 = d1 – 2,4m = m*( q – 2,4); длину нарезанной части червяка b1 принимают b1 ≥ (11 + 0,06 z2).
d2 = m* z2; da2 = d2 + 2 m = m*( z2 + 2); df2 = d2 – 2,4m = m*( z2 – 2,4); наибольший диаметр червячного колеса определяют по формуле
dam2 ≤ da2 + 6 m/( z1 +2); ширина венца колеса b2 ≤ 0,75 da1.
Коэффициент полезного действия червячного редуктора с учетом потерь в зацеплении и в опорах определяется по формуле
η = (0,95…0,96)*tq γ/[tq(γ + φ')] , (4.24)
где φ' – приведенный угол трения. КПД возрастает с увеличением числа заходов червяка, поскольку увеличивается γ. Приведенный угол трения очень сильно зависит от скорости скольжения
,
(4.25)
где v1 = 0,5ω1*d1*10 –3 и v2 = 0,5ω2*d2*10 –3 – окружные скорости червяка и колеса, м/с; ω1 и ω2 – угловые скорости червяка и колеса, рад/с.
При увеличении скорости скольжения от 0,01 м/с до 15 м/с приведенный угол трения уменьшается от 60 до 10, а следовательно повышается КПД.
В червячной передаче наиболее слабым звеном является колесо, поэтому прочностные расчеты проводят именно червячного колеса. Расчеты выполняются в такой последовательности.
Известно: Т2; u = z2/ z1; принимаете сами z1 и q; выбираете материал колеса и по рекомендациям или задавшись коэффициентом запаса прочности определяете [σ]H.
Определяете межосевое расстояние по формуле
,
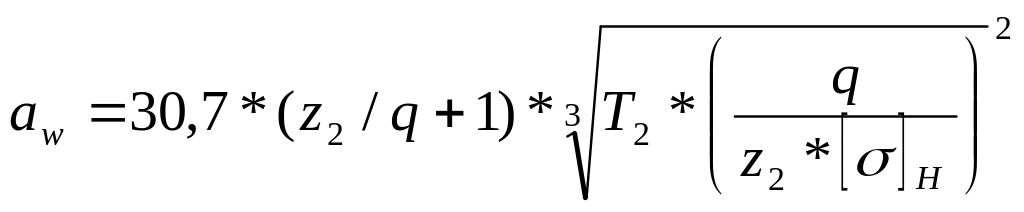(4.26)
где Т2 – крутящий момент на валу колеса, Н*мм (определяется из кинематического расчета).
Учитывая, что aw = (d1 + d2) / 2 = m*( q + z2)/2, (4.27)
m = 2 aw/*( q + z2) (4.28)
Затем определяете все остальные параметры (элементы) передачи по формулам, приведенным выше.
В заключение проводим проверку выполнения условия прочности на изгиб
σF = 1,5YF*KFβ*KFv*cos γ*T2/(d1*d2*m) ≤ [σ]F (4.29)
Все коэффициенты и допустимое напряжение берем из литературы.
В случае не выполнения условия прочности, определяем модуль по формуле
(4.30)