2. Передаточное отношение, передаточное число

Передаточное отношение – это отношение мгновенных угловых или линейных скоростей ведущего и ведомого звеньев. u = ω₁/ω₂.

Передаточное число – это отношение чисел зубьев или диаметров (радиусов) ведомого и ведущего звеньев. i = z₂/z₁.

В производственном лексиконе эти два понятия зачастую путают, поскольку в численном выражении u = i. Определим u и i при последовательном и параллельном соединении зубчатых колес.

Последовательное соединение (рис.4.3).

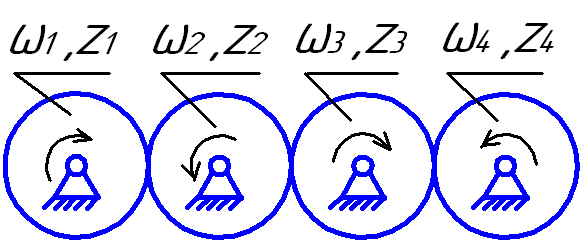u _1-4 = ω₁/ω₂* ω₂/ω₃* ω₃/ω₄ = ω₁/ω₄

i _1-4 = z₂/z₁* z₃/z₂* z₄/z₃ = z₄/z₁

Видим, что промежуточные шестерни z₂ и z₃ не влияют на передаточное отношение и передаточное число. Эти шестерни называются паразитными. Они

Рис. 4.3 устанавливаются в двух случаях:

1 – для изменения направления вращения; 2 – для получения большого межосевого расстояния при малых поперечных габаритах передачи.

Параллельное соединение (рис.4.4).

u _1-4 = ω₁/ω₂* ω₃/ω₄ = ω₁/ω₄,

ω₂ = ω₃ – это один вал.

i _1-4 = z₂/z₁* z₄/z₃

При параллельном соединении нет паразитных шестеренок. Больше того, у зубчатых колес 1-й ступени (z₁ и z₂) модуль меньше чем модуль колес 2-й ступени (z₃ и z₄), поскольку крутящий момент на входе 1-й ступени в i _1-2 = z₂/z₁ раз меньше момента на входе 2-й ступени (при условии, что обе

Рис. 4.4 ступени редукторные, то есть

z₂ > z_{1 ;} z₄ > z₃ , соответственно i _1-2 > 1 и i _3-4 > 1).

Редуктор –понижает обороты, но увеличивает крутящий момент.

Мультипликатор – повышает обороты, но понижает крутящий момент.

3. Силы в зацеплении цилиндрических зубчатых колес

В цилиндрической косозубой передаче силу в зацеплении раскладывают на составляющие (рис.4.5).

Окружная сила F_t определяется по формуле

F_t = 2T₁/d₁ , (4.1)

где T₁ – крутящий момент на валу шестерни;

d₁ – делительный диаметр шестерни .

Радиальная сила равна

F_r = F_t*tq α/cos β , (4.2)

Рис. 4.5

где α = 20^о – стандартный угол эвольвентного зацепления; β – угол наклона зубьев.

Осевая сила равна

F_а = F_t*tq β (4.3)

В цилиндрической прямозубой передаче β = 0, поэтому F_r = F_t*tq α, а F_а = 0.

4. Прочностной расчет цилиндрических зубчатых передач

В инженерной практике может возникнуть необходимость в двух видах расчетов: проверочном и проектировочном. В первом случае Вам известны все элементы передачи, а так же крутящие моменты на валах. Задача – определить напряжения и сравнить с допустимыми. Во втором случае необходимо найти элементы передачи, удовлетворяющие условию прочности.

Зубчатые передачи рассчитывают на контактную прочность (σ_H ≤ [σ_H]) и на изгиб зубьев (σ_F ≤ [σ_F]) .

1. Расчет зубьев на контактную прочность

Расчеты на контактную прочность базируются на формуле Герца

, (4.4)

где q – нагрузка на единицу длины контактной линии;

Е = 2*Е₁*Е₂/( Е₁+Е₂) – приведенный модуль упругости материалов зубчатых колес; ρ_пр = ρ₁*ρ₂/( ρ₁+ρ₂) – приведенный радиус кривизны контактирующих элементов; μ – коэффициент Пуассона.

Опуская промежуточные выкладки (они описаны в приведенной литературе), запишем условия контактной прочности: прямозубых передач

; (4.5)

косозубых передач

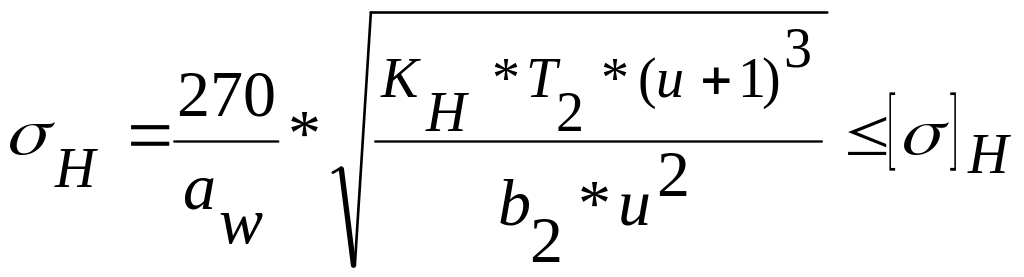. (4.6)

Здесь a_w = a – межосевое расстояние; Т₂ – крутящий момент на валу зубчатого колеса;

b₂ – ширина колеса; u – передаточное отношение пары зацепления;

K_H = K_Ha* K_Hβ* K_Hv – комплексный коэффициент. K_Ha – учитывает неравномерность распределения нагрузки между зубьями; K_Hβ – учитывает неравномерность распределения нагрузки по ширине венца; K_Hv – зависит от скорости и степени точности передачи. Значения коэффициентов даны в литературе.

Допускаемое контактное напряжение [σ]_H определяется по формуле

[σ]_H = σ_{Н lim b}*K_НL/[n]_Н , (4.7)

где σ_{Н lim b} – предел контактной выносливости при базовом числе циклов нагружения;

K_НL – коэффициент, учитывающий число циклов ( в большинстве случаев принимают K_НL = 1); [n]_Н – коэффициент безопасности; для колес из нормализованной и улучшенной стали, а также при объемной закалке принимают [n]_Н = 1,1…1,2; при поверхностном упрочнении зубьев [n]_Н = 1,2…1,3.

σ_{Н lim b} определяются по формулам (см. таблицу 4.1).

Таблица 4.1

Способы термохимической обработки зубьев	Твердость поверхностей зубьев	Сталь	σН lim b, МПа
Нормализация или улучшение	< НВ 350	Углеродистая и легированная	2 НВ + 70
Объемная закалка	38…50 НRС	Углеродистая и легированная	18 НRС + 150
Поверхностная закалка	48…54 НRС	Углеродистая и легированная	17 НRС + 200
Цементация и нитроцементация	56…63 НRС	Низкоуглеродистая	23 НRС
Азотирование	57…67 НRС	Легированная (38ХМЮА)	1050

В таблице НВ – твердость по Бринеллю; НRС – твердость по Роквеллу. 1 НRС ≈ 10 НВ

Предположим, Вы применили углеродистую Сталь 45, термообработка – нормализация, твердость НВ 200. Тогда σ_{Н lim b} = 2 НВ + 70 = 470 МПа. Эта же сталь при объемной закалке может дать твердость 40 НRС. В этом случае

σ_{Н lim b} = 18 НRС + 150 = 870 МПа. А если Вы применили Сталь 12ХН3А, термообработка – цементация и закалка, твердость 60 НRС, то

σ_{Н lim b} = 23 НRС = 1380 МПа. Разница весьма существенная. Учитывая, что межосевое расстояние (a_w) обратно пропорционально допускаемому напряжению (формулы 4.5 и 4.6), габаритные размеры в 1-м и 3-ем случаях будут отличаться почти в 3 раза. Если бы шестерни в коробках передач автомобилей делали из не термообработанной стали, то коробки пришлось бы возить в кузове.

Для косозубых передач рекомендуется допускаемое контактное напряжение определять по формуле

[σ]_H = 0,45*([σ]_H1 + [σ]_H2), (4.8)

где [σ]_H1 и [σ]_H2 – допускаемые контактные напряжения соответственно для шестерни и колеса.

По формулам (4.5) и (4.6) проводится проверочный расчет. При проектировочном расчете из формул выделяют a_w. При этом ширина колеса b₂ заменяется выражением b₂ = Ψ_ba* a_w. Ψ_ba – коэффициент ширины зубчатого венца. Рекомендуется:

для прямозубых передач Ψ_ba = 0,125…0,25; для косозубых передач

Ψ_ba = 0,25…0,40. В результате получают формулы для проектировочного расчета:

прямозубых передач

(4.9)

косозубых передач

(4.10)

В формулах (4.5); (4.6); (4.9); (4.10) для получения требуемой размерности крутящий момент Т₂ следует подставлять в Н*мм.

После определения межосевого расстояния выбирают стандартный нормальный модуль в интервале

m = m_n = (0,01…0,02)*a_w..

Определяют суммарное число зубьев, предварительно задавшись углом наклона зубьев (для косозубых колес) в интервале β = 8…15^о.

z_∑ = 2*a_w*cos β/m_n (4.11)

Определяют числа зубьев шестерни и колеса

z ₁ = z_∑/(u + 1); z ₂ = z ₁* u (4.12)

При расчетах числа зубьев могут получиться не целыми. Их округляют до ближайших целых чисел и уточняют: для прямозубых передач – межосевое расстояние; для косозубых – угол наклона зубьев.

Затем, по зависимостям, приведенным в п.4.1.1, определяют все остальные элементы шестерни и колеса.

В завершение проводят проверку контактных напряжений по формулам (4.5) или (4.6). В случае невыполнения условия прочности увеличивают b₂ (при малых расхождениях σ_H и [σ]_H) или увеличивают a_w (при значительных расхождениях σ_H и [σ]_H).