IV Детали машин

Курс «Детали машин» завершает цикл общеинженерных дисциплин и одновременно является первым из расчетно-конструкторских курсов, в котором изучают основы проектирования машин и механизмов.

В курсе изучают детали (узлы) машин общего назначения, то есть такие, которые встречаются во всех машинах и механизмах или в большинстве из них. К таким деталям (узлам) относятся: передачи (зубчатые, червячные, фрикционные, гибкой связью); соединения (разъемные, не разъемные); валы, оси; подшипники качения и скольжения; муфты; пружины. Этот перечень говорит об объеме курса. Естественно, что по курсу имеется достаточно много литературы, как учебной, так и вспомогательной (различные справочники, атласы конструкций и др.).

В нашем курсе «Прикладная механика» дисциплина «Детали машин» входит всего лишь заключительным разделом. Очевидно, что мы не сможем «объять необъятное». Сконцентрируем наше внимание на методике элементарных расчетов и возможности практического (прикладного) применения полученных знаний.

1. Зубчатые передачи.

1. Элементы зубчатых колес.

В паре зубчатого зацепления колесо с меньшим числом зубьев обычно называют шестерней, с большим – зубчатым колесом. Большинство зубчатых колес имеют эвольвентный профиль зуба.

Э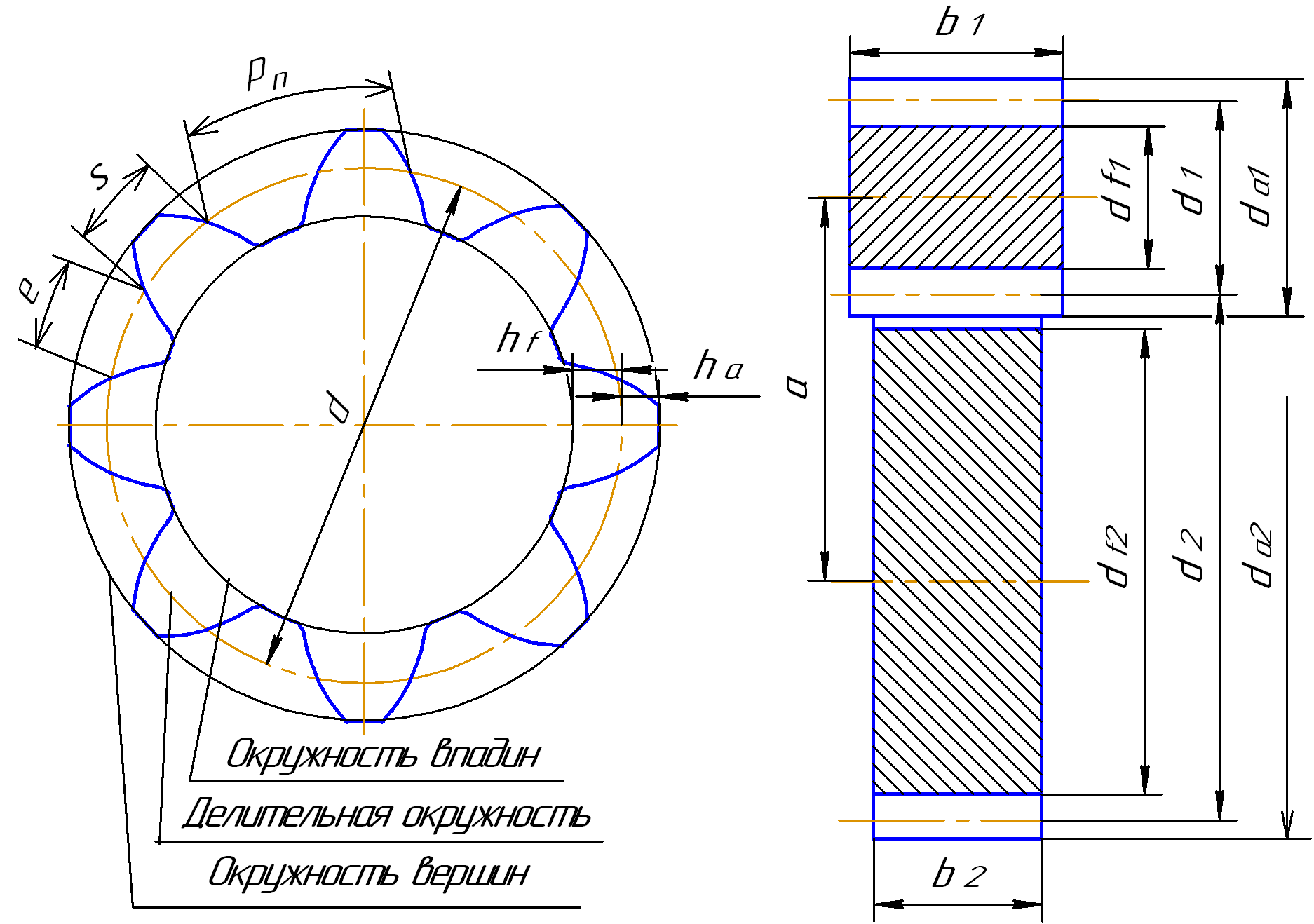 вольвентой называется кривая, которую описывает любая точка прямой линии, прокатываемой по окружности без скольжения. Сама окружность называется основной окружностью или эволютой.

Основные геометрические параметры (элементы) зубчатых колес показаны на рис.4.1. Индекс 1 относится к шестерне, индекс 2 – к колесу.

Рис. 4.1

d₁, d₂ – делительные диаметры; d_a1, d_a2 – диаметры вершин зубьев; d_f1, d_f2 – диаметры впадин зубьев; a – межосевое расстояние; b₁ – ширина шестерни;

b₂ – ширина колеса; h_a – высота головки зуба; h_f – высота ножки зуба; s – толщина зуба; e – ширина впадины; p_n – нормальный шаг зубьев; z₁, z₂ – числа зубьев.

Длина делительной окружности равна πd, с другой стороны она равна p_n*z, следовательно d = (p_n/π)* z. Величина m = p_n/π называется нормальным модулем или просто модулем зубчатого колеса. Модуль является основным, самым главным параметром зубчатого колеса, все остальные зависят от него. Модуль – величина стандартизованная, то есть существует стандартный ряд модулей, отступление от которого не допускается, иначе колесо не будет нарезано, поскольку весь зуборезный инструмент модульный.

Как только определился модуль, все остальные элементы приобретают вид:

d = m* z; h_a = m; h_f = 1,25 m; d_a = d + 2 h_a = m*( z + 2);

d_f = d - 2 h_f = m*( z – 2,5); p_n = m*π;

s ≈ e = p_n/2 = m*π/2; a = (d₁ + d₂)/2 = m*( z₁ + z₂)/2;

b₂ = ψ_ba* a = ψ_ba* m*( z₁ + z₂)/2, где ψ_ba = b₂/ a – рекомендуемая величина.

Ширина шестерни b₁ берется больше ширины колеса на 2…10 мм с тем, чтобы даже при небольшом осевом смещении в процессе сборки или эксплуатации колесо находилось в зацеплении с шестерней по всей ширине. То есть

b₁ = b₂ + (2…10) = ψ_ba* m*( z₁ + z₂)/2 + (2…10) .

Видим, что все геометрические параметры (элементы) зубчатых колес зависят от модуля.

Все, приведенные выше данные, относятся к прямозубым колесам. Для косозубых цилиндрических колес (рис.4.2) нужно учитывать угол наклона зубьев β. На рис.4.2 зубья условно срезаны до делительной окружности.

Для косозубых колес вводится понятие окружной шаг p_t. Из рисунка видим, что p_t = p_n/cosβ. Величина m_t = p_t/π называется окружным модулем. Очевидно соотношение m = m_t* cosβ или m_t = m/ cosβ.

Подставив в формулы параметров (кроме h_a и h_f) вместо m - m_t, получим размеры элементов

Рис.4.2 косозубой передачи, в частности

d = m* z/ cosβ; d_a = m*z / cosβ + 2 m; d_f = m*z / cosβ – 2,5 m.

h_a = m и h_f = 1,25 m не зависят от вида передачи (прямозубая или косозубая).

Практические способы определения модуля.

В инженерной практике не редки случаи, когда возникает необходимость определения модуля вышедшей из строя шестерни с тем, чтобы изготовить новую шестерню. Применяется два способа: а) измеряют окружной шаг и угол наклона зубьев β (если шестерня косозубая); б) измеряют диаметр вершин зубьев. Определяют модуль: а) m = p_t * cosβ/ π; б) m = d_a/( z / cosβ + 2).

Полученные значения модуля округляют до ближайшего стандартного значения.