1. Определение положений и перемещений звеньев механизма

Решение задачи проведем графическим и аналитическим методами. В качестве примера возьмем кривошипно-ползунный механизм.

Дано: длина кривошипа r = 150 мм; длина шатуна l = 450 мм; ведущий кривошип (ω = const.)

Положение кривошипа задается углом φ. Цикл движения такого механизма осуществляется за один полный оборот кривошипа – период цикла Т = 60/n = 2π/ω, с. Где n - число оборотов в минуту; ω – угловая скорость, с^-1. При этом φ = 2π, рад.

Вычерчиваем кинематическую схему механизма в выбранном масштабе (рис.3.5). На рис.3.5 принят масштаб 1:10. Строим схему механизма в восьми положениях кривошипа (чем больше положений механизма, тем выше точность полученных результатов). Отмечаем положение ползуна (рабочее звено). По полученным данным строим график зависимости перемещения точки В ползуна от угла поворота кривошипа φ (S_В = f(φ)). Этот график называется кинематической диаграммой перемещений точки В.

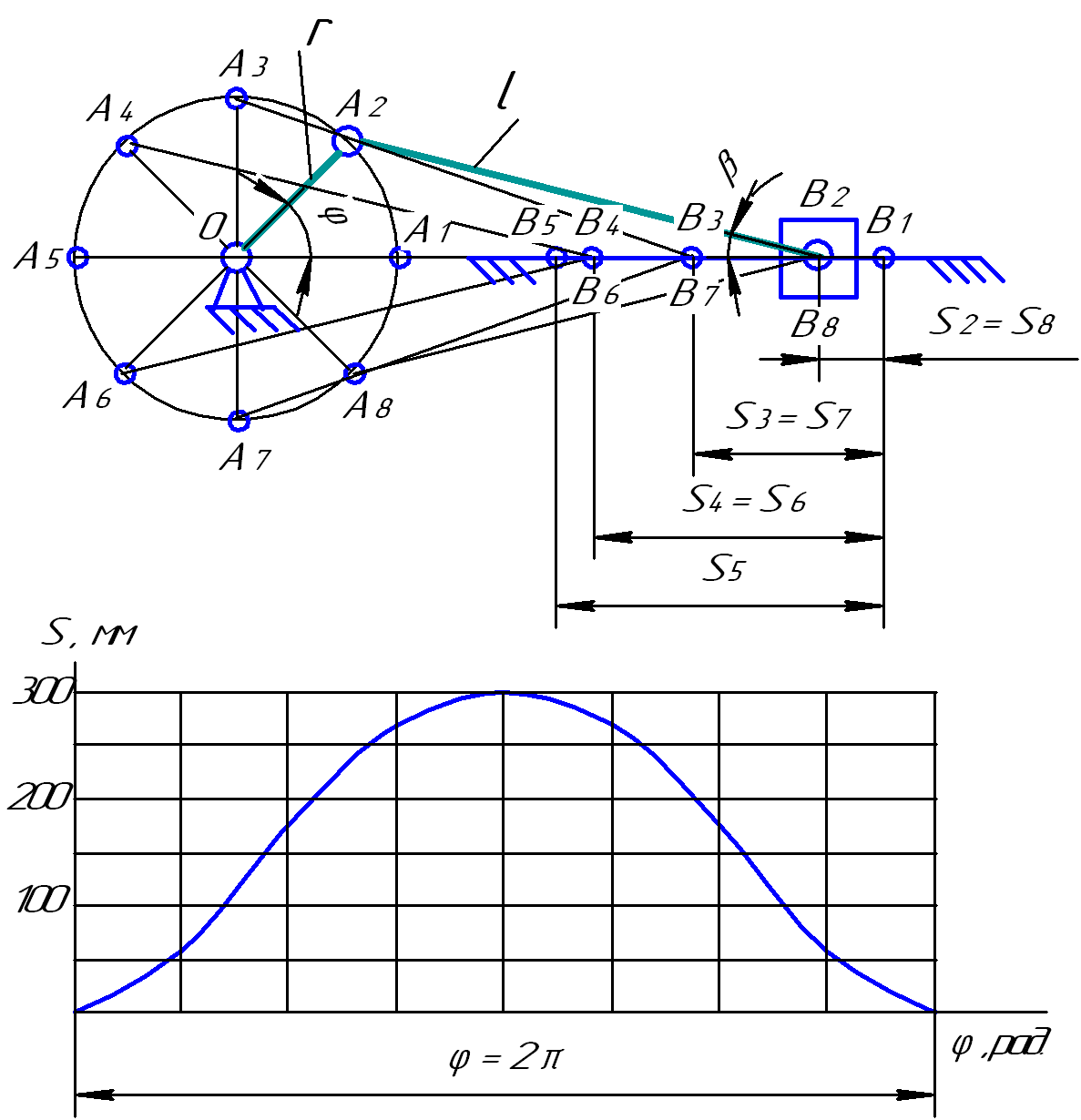
Аналитический метод

Перемещение ползуна отсчитывается от крайнего правого положения (рис.3.5). Анализируя рисунок, можно записать уравнения

S =(r+l)–(r*cosφ+l*cosβ) (3.1)

r*sin φ = l*sin β

Обозначив r/ l = λ, можно записать

β = arcsin(λ* sin φ).

Следовательно, для каждого угла φ не сложно определить соответствующий угол β, а затем решить первое уравнение системы (3.1). При

Рис. 3.5 этом точность результатов будет определяться только заданной точностью расчетов.

В [1] приведена приближенная формула для определения перемещений ползуна

S = r*(1 - cos φ + sin² φ* λ /2) (3.2)

2. Определение скоростей и ускорений точек и звеньев механизма

Скорости и ускорения ведомых звеньев механизма могут быть определены методами планов, кинематических диаграмм и аналитическими. Во всех случаях в качестве исходных должны быть известны: схема механизма при определенном положении ведущего звена, его скорость и ускорение.

Рассмотрим применение указанных методов на примере кривошипно-ползунного механизма (рис.3.5) при φ = 45^о и n = 1200 об/мин, соответственно ω = π*n/30 = 125,7 с^-1.

План скоростей (ускорений) механизма.

Планом скоростей (ускорений) механизма называется фигура, образованная векторами скоростей (ускорений) точек звеньев при заданном положении механизма.

Построение плана скоростей

Известно

По величине V_АО = ω* r = 125,7*0,15 = 18,9 м/с.

Выбираем масштаб построения, например, 1м/(с*мм).

Отмечаем какую-нибудь точку в качестве полюса Р при построении плана скоростей (рис.3.6).

От полюса откладываем вектор ,

Рис. 3.6 перпендикулярно АО. Вектор скорости точки В находим путем графического решения уравнения Известно направление векторов. Вектор лежит на горизонтальной прямой, а вектор перпендикулярен ВА. Из полюса и конца вектора проводим соответствующие прямые и замыкаем векторное уравнение. Замеряем расстояние Pb и ba и, с учетом масштаба, находим

V_В = 16,6 м/с, V_ВА = 13,8 м/с.

Построение плана ускорений (рис.3.7)

Ускорение точки А равно , поскольку = 0. . По величине нормальное ускорение aⁿ_АО = ω²* r =

= 125,7²*0,15 = 2370 м/с².

Касательное ускорение a^t_АО = ε* r = 0, так как угловое ускорение ε = 0, поскольку ω = const.

Рис. 3.7

Выбираем масштаб построения, например, 100м/(с²*мм). Откладываем от полюса р_а вектор , параллельный АО от А к О. Вектор ускорения точки В находим путем графического решения уравнения . Вектор направлен параллельно ВА от В к А, его величина равна aⁿ_ВА = V_ВА²/ l = 13,8²/0,45 = 423 м/с².

a_В = 1740 м/с²; a^t_ВА = 1650 м/с².

Метод кинематических диаграмм (рис.3.8)

Метод кинематических диаграмм – это графический метод. Он включает в себя графическое дифференци-рование сначала графика перемещений, а затем графика скорости. При этом кривые перемещений и скорости заменяются ломаной линией. Значение средней скорости на элементарном участке пути можно выразить в виде

µ_S – масштаб перемещения.

µ_t – масштаб времени.

В нашем случае

µ_S = 0,01 м/мм;

µ _t = 0,000625 с/мм.

Масштаб скорости равен

µ_V = µ_S/(µ _t*H_V) =

0,01/(0,000625*30) =

= 0,533 м/(с*мм).

Масштаб ускорения равен

µ_а = µ_V/(µ _t* H_а) =

0,533/(0,000625*30) =

= 28,44 м/(с²*мм).

Порядок построения диаграммы скорости.

На расстоянии H_V (20…40мм) ставится точка О – полюс построения. Из полюса проводятся прямые, параллельные отрезкам ломаной линии графика перемещения, до пересечения оси ординат. Ординаты переносятся на график скорости в середину соответствующих участков. По полученным точкам проводится кривая – это и есть диаграмма скорости.

Диаграмма ускорения строится аналогично, только исходным графиком становится диаграмма скорости, замененная ломаной линией.

Для указания численных значений скорости и ускорения рассчитывается масштаб построения, как показано выше.

Скорости и ускорения ползуна можно определить и аналитическим способом, путем последовательного дифференцирования приближенного уравнения (3.2).

(3.3)

(3.4)

Знание скоростей и ускорений звеньев механизма необходимо для динамического анализа механизма, в частности, для определения сил инерции, которые могут при больших ускорениях (как в нашем случае) многократно превышать статические нагрузки, например, вес звена.

Ввиду краткости нашего курса, мы не проводим силовое исследование механизмов, но Вы самостоятельно можете ознакомиться с ним по литературе, в частности, рекомендованной в этом разделе.

В теории механизмов и машин рассматриваются вопросы геометрии зубчатого зацепления, а так же вопросы трения в кинематических парах. Мы тоже рассмотрим эти вопросы, но в разделе « детали машин », применительно к конкретным случаям и задачам.

Литература

1. Первицкий Ю.Д. Расчет и конструирование точных механизмов. – Л.: Машиностроение,

1976. – 456 с.

2. Заблонский К.И. Прикладная механика. – Киев : Вища школа, 1984. – 280 с.

3. Королев П.В. Теория механизмов и машин. Конспект лекций. – Иркутск : Издательство

ИрГТУ, 2001. – 104 с.