4. Структурный синтез и анализ механизмов

Структурный синтез механизмов является начальной стадией составления схемы механизма, удовлетворяющего заданным условиям. Исходными данными обычно являются виды движения ведущего и рабочего звеньев механизма. Если элементарный трех- или четырехзвенный механизм не решает задачу требуемого преобразования движения, схема механизма составляется путем последовательного соединения нескольких элементарных механизмов.

Основные принципы структурного синтеза и анализа механизмов с КП 5-го класса и классификацию таких механизмов впервые предложил русский ученый Л.В. Ассур в 1914году, а развил идеи Л.В. Ассура академик И.И. Артоболевский. Согласно предложенной классификации механизмы объединяются в классы от первого и выше по структурным признакам. Механизм первого класса состоит из ведущего звена и стойки, соединенных кинематической парой 5-го класса. Механизмы более высоких классов образуются последовательным присоединением к механизму первого класса кинематических цепей, не изменяющих степени подвижности исходного механизма, то есть имеющих степень подвижности, равную нулю. Такая кинематическая цепь называется структурной группой. Поскольку в структурную группу входят только КП 5-го класса, а степень подвижности группы равна нулю, то можно записать

W = 3n - 2P₅ = 0, откуда P₅ = 3/2 n.

Следовательно, в структурную группу может входить только четное число звеньев, поскольку P₅ может быть только целым числом.

Структурные группы различают по классу и порядку. Группа 2-го класса и 2-го порядка состоит из двух звеньев и трех КП. Класс группы (выше 2-го) определяется числом внутренних КП, образующих подвижный замкнутый контур из наибольшего числа звеньев группы.

Порядок группы определяется числом свободных элементов звеньев, которыми группа присоединяется к механизму.

На рис.3.4 показан механизм 1-го класса, а так же структурные группы 2-го и 3-го классов. В результате структурного синтеза (присоединение структурных групп к механизму 1-го класса) получены четырехзвенные механизмы 2-го класса и шестизвенный механизм 3-го класса (рис.3.4).

При структурном анализе определяется степень подвижности механизма и разложение его кинематической цепи на структурные группы и ведущие звенья. При этом удаляются лишние степени свободы (если они есть) и пассивные связи (при их наличии).

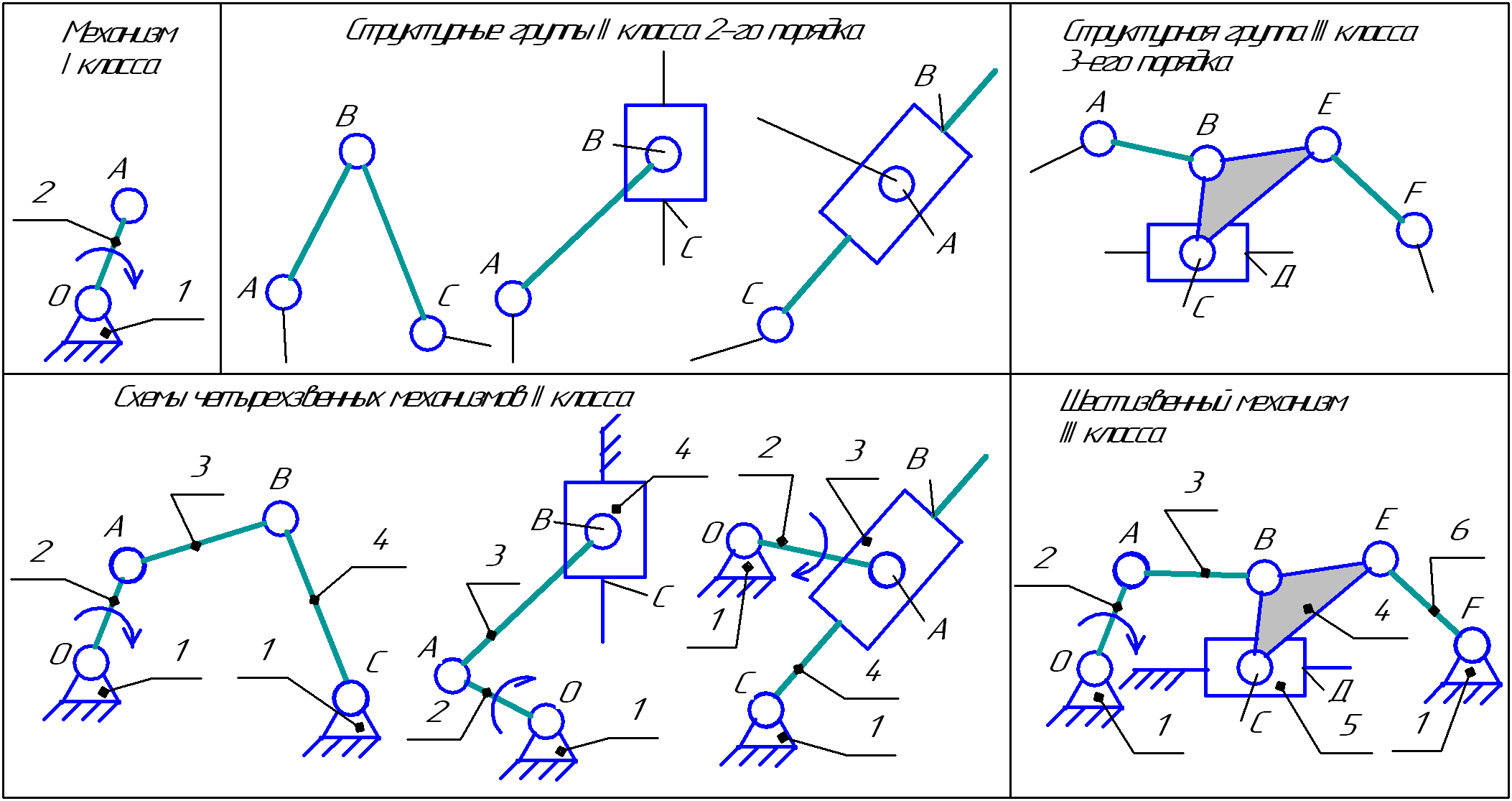
Рис. 3.4

2. Кинематический анализ механизмов

Целью кинематического анализа является изучение движения звеньев механизма независимо от действующих на них сил. При этом принимаются допущения: звенья абсолютно жесткие и в кинематических парах отсутствуют зазоры.

Решаются следующие основные задачи: а) определение положений звеньев и построение траекторий движения отдельных точек или звеньев в целом; б) нахождение линейных скоростей точек механизма и угловых скоростей звеньев; в) определение линейных ускорений точек механизма и угловых ускорений звеньев.

Исходными данными являются: кинематическая схема механизма; размеры всех звеньев; законы движения ведущих звеньев.

При кинематическом анализе механизмов используются аналитические, графоаналитические и графические методы. Обычно рассматривается полный цикл движения механизма.

Результаты кинематического анализа позволяют при необходимости скорректировать схему механизма, кроме того, они необходимы для решения задач динамики механизма.