
- •Первый тип задач на касательную
- •3) Найдём y’
- •1). Уравнение касательной имеет вид:
- •4). Получим уравнение касательной
- •Второй тип задач на касательную.
- •Третий тип задач на касательную – это геометрический смысл производной функции в точке.
- •Четвертый тип задач на касательную
- •Пятый тип задач на касательную - уравнение общей касательной нескольких кривых
- •Шестой тип задач на касательную – расстояние между кривыми.
Пятый тип задач на касательную - уравнение общей касательной нескольких кривых
Говорят, что прямая y=kx + b является общей касательной графиков функций y=f1(x) и y=f2(x), если она касается как одного, так и другого графиков, но не обязательно в одной и той же точке.
Правило.
Функции y=f1(x) и y=f2(x) имеют в точке пересечения M(x0;y0) общую невертикальную касательную, если
f1’(x0) = f2’(x0)
ЗАДАЧА. Докажите, что параболы y1=3x²-5x-2 и y2=2x²-x-6 имеют в их общей точке общую касательную. Найти уравнение этой общей касательной.
Найдем точку пересечения парабол
3x²-5x-2 = 2x²-x-6
x²-4x+4 = 0
(x-2)² = 0
x = 2
y(2)= 2·4-2-6=0 y(2)=3·4-5·2-2=0
значит, у парабол одна точка пересечения (2;0)
Теперь перейдем к составлению уравнений касательных
y(1)=6x -5 y(1)(2) = 12-5=7
y(2)=4x-1 y(2)(2) = 8-1=7
Получим уравнение касательной
y=0+7(x-2)
y=7x-14
Ответ: y=7x-14
ЗАДАЧА. Найти уравнение всех общих касательных к графикам функции y=x²+1 и y=4x²-2
Составим уравнение касательной в точке x0 = a к графику
y=x²+1
y(a)=a²+1
y’=2x
y’(a)=2a
Получим уравнение касательной
y=a²+1+2a(x-a)
y=a²+1+2ax-2a²
y=2ax-a²+1
Составим уравнение касательной в точке с абсциссой x0=b к графику y=4x²-2
y(b)=4b²-2
y’=8x
y’(b)=8b
Получим уравнение касательной
y=4b²-2+8b(x-b)
y= 4b²-2+8bx-8b²
y=8bx-4b²-2
Уравнения прямых совпадают, если угловые коэффициенты и свободные члены равны, т.е.
![]()
![]()
Подставим a=4b во второе уравнение, получим
-16b2 +1 = -4b2 -2
12b2 = 3
b2
= ![]()
![]()
![]()
Получим уравнения касательных
y=4x-3 y=-4x-3
Ответ: y=4x-3 y=-4x-3
Шестой тип задач на касательную – расстояние между кривыми.
Пусть дана функция y = f(x) и прямая y = kx +b, тогда можно составить уравнение касательной, параллельной данной прямой. Проведенная касательная разделит плоскость на две части: в одной из них будет находиться заданная прямая, а в другой график функции y = f(x).
Кратчайшее расстояние между кривой y = f(x) и прямой y = kx +b можно посчитать по формуле :
![]() =
=
![]()
Задача. Найти
кратчайшее расстояние между параболой
y
= x2
и прямой y
= ![]()
Убедимся, что графики не имеют общих точек, для этого решим уравнение:
x2
=![]() ,
,
3x2 – 4x +6 = 0,
D = 16-72< 0.
Нет корней, нет общих точек.
Найдем точку, в которой касательная параллельна прямой y =

y = x2,
y’ = 2x,
2x = ![]() ,
,
x= ![]() ,
,
x0 = ,
y0
= ![]() .
.
Получим касательную y =

y
= ![]()
Прямая y
= ![]() и парабола y
= x2
лежат по разные стороны от касательной
y
=
,
тогда расстояние от прямой y
=
до параболы y
= x2,
это расстояние от точки M
(x0;y0),
лежащей на параболе, до прямой y
=
,
находим его по формуле
и парабола y
= x2
лежат по разные стороны от касательной
y
=
,
тогда расстояние от прямой y
=
до параболы y
= x2,
это расстояние от точки M
(x0;y0),
лежащей на параболе, до прямой y
=
,
находим его по формуле
![]() =
=
![]() =
=  .
.
Ответ: ![]()
Задача. Найти
расстояние между касательными к графику
функции ![]() ,
образующими с положительным направлением
оси Ох угол 450.
,
образующими с положительным направлением
оси Ох угол 450.
y’ =
 =
= 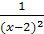
y0’ = tg 450
= 1
![]()
x= 3 x= 1
x0= 3 x0= 1
Составим уравнение касательной в точке x0= 3
y(3) = 0
y = 0 +
1![]() (x-3)
(x-3)
y = x-3
Составим уравнение касательной в точке x0= 1
y(1) = 2
y = 2 + 1 (x-3)
y = x+1
Пусть y = x +1 – данная прямая,
![]() - данная кривая,
- данная кривая,
y = x-3 - данная касательная,
=
![]()
Ответ : ![]()
