Четвертый тип задач на касательную

В задачах этого типа необходимо составить уравнение касательной к графику y = f(x), проходящей через заданную точку М(х;у), не лежащую на данной кривой y= f(x)

№ 845 Мордкович А.Г.

Через точку В провести касательную к графику функции y = f(x), если

f(x) = _, В(-2:3)

1. Проверим, проходит ли график у = через точку В(-2;3)

у(-2) = = ≠ 3, значит точка В не является точкой касания.

2. Составим уравнение касательной в точке х₀

   1. у₀ =

б) у’ = -

=

в) Получим уравнение касательной

у = - (х - х₀)

3. Полученная касательная проходит через точку В(-2:3) т.е.

3 = - (-2- х₀)

Решим полученное уравнение, которое определено,

если 3 – х > 0

х₀ < 3

6 = 2(3- х₀) + 2 + х₀

6 = 6 - 2х₀ + 2 + х₀

6 = 8 - х₀

Уравнение равносильно системе:

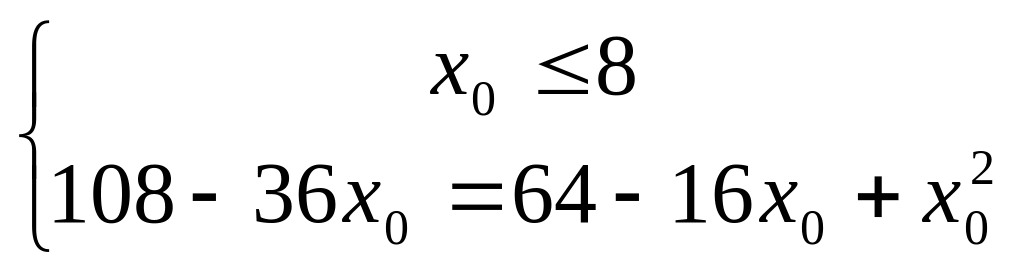
1. + 20х₀ – 44 = 0

х₀ = -22 х₀ = 2

Получили две точки касания при х₀ = -22 х₀ = 2

у = 8 + (х - )

у = 8 + х -

у = х + - 7

1. Касательная проходит через точку (1;3) значит

3 = + - 7

= 4 + 4 -

4 - + 4 = 0

2 - + 2 = 0

4. При х₀ = -22 уравнение касательной имеет вид:

у = - (х + 22)

у = 5 - (х + 22)

у = -0,1х + 2,8

5. При х₀ = 2 уравнение касательной имеет вид:

у = - (х - 2)

у = 1 - (х - 2)

у = -0,5х + 2

Ответ: у = -0,5х + 2 ;

у = -0,1х + 2,8

Задача:

Найти уравнение прямой проходящей через точку (1:3) касающуюся графика функции у = 8 и пересекающий в двух различных точках график функции у =

2. Точка (1:3) не является точкой касания, т.к.

3. Составим уравнение касательной к графику у = 8 в точке

1. = 8

б) у’ =

в)

г) Получим уравнение касательной

b = 1 b = 4

= = 2

4. При = получим уравнение касательной:

у = (4: ) х + 4∙ - 7

у = 8х – 5

5. Проверим, сколько точек пересечения у прямой у = 8х – 5 с параболой у = х² + 4х – 1

х² + 4х – 1 = 8х – 5

(х-2)² = 0

х-2 = 0

х = 2

Одна точка пересечения

6. При = 2, получим уравнение касательной:

у = х + 4∙2 – 7

у = 2х + 1

7. Проверим сколько точек пересечения имеет прямая у = 2х + 1 с параболой у = х² + 4х – 1

х² + 4х – 1 = 2х + 1

х² + 2х – 2 = 0

D = 4 +8 = 12

х = - = -1 - х = -1 +

Получили две точки пересечения.

Ответ: у = 2х + 1