
- •Первый тип задач на касательную
- •3) Найдём y’
- •1). Уравнение касательной имеет вид:
- •4). Получим уравнение касательной
- •Второй тип задач на касательную.
- •Третий тип задач на касательную – это геометрический смысл производной функции в точке.
- •Четвертый тип задач на касательную
- •Пятый тип задач на касательную - уравнение общей касательной нескольких кривых
- •Шестой тип задач на касательную – расстояние между кривыми.
Третий тип задач на касательную – это геометрический смысл производной функции в точке.
Вспомним геометрический смысл производной в точке, т.е. если прямая y= kx+ b является касательной к графику функции y=f(x) в точке с абсциссой x=x0, то величина угла φ между этой прямой и положительным направлением оси Ох удовлетворяет соотношению
k=tgφ = f’ (х0)
Отсюда находим, что
![]()
№ 814г Мордкович А.Г.
Найти угловой
коэффициент касательной, проведенной
к графику функции y
= ![]() в точке x0
= 1
в точке x0
= 1
y ’ =
 =
=  =
= 
y0’ = y’(1) =

k = y0’ =

Ответ: 0,75
Задача. Найти
тангенс угла наклона касательной к
графику функции y
= ![]() в точке х0=1
в точке х0=1
 =
=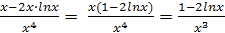
y0’ = y(1) =

tg
 = y0’
=1
= y0’
=1
Ответ: tg = 1
Правило.
Углом между графиком функции y=(f) в точке x0 и осью 0х называется угол между положительным направлением оси 0х и касательной к графику функции в точке х=х0 такой, что f(x0)=0.
Задача. Под каким углом график функции y=sinx
пересекает ось абсцисс в точке х0=0?
1) y’=cos x
2) y’0 = y’(0) = cos0 = 1
3) tg = y0’ =1
4) tg = 1
=450
Ответ : 450
Задача. Найти
координаты точек пересечения с осями
координат тех касательных к графику
функции y
=![]() ,
у которых угловой коэффициент равен 4.
,
у которых угловой коэффициент равен 4.
Пусть (х0; f(x0)) – точка графика функции y =
 ,
в которой касательная к ее графику
имеет угловой коэффициент, равный 4, а
y
= kx
+ b
уравнение этой касательной.
,
в которой касательная к ее графику
имеет угловой коэффициент, равный 4, а
y
= kx
+ b
уравнение этой касательной.
Тогда k = f ‘(x0) = 4
f ’(x)
=![]() =
= ![]()
f ’(x0) =
 = 4
= 4
(x0+1)2=1
x0+1=1 x0+1= -1
x0=0 x0= -2
Составим уравнение касательной в каждой точке х0
Пусть х0=0
f(x0)=-2, тогда получим уравнение касательной
у = -2+4(х-0)
у = 4х-2
Пусть х0=-2
f
(x0)
= ![]() = 6,
= 6,
тогда получим уравнение касательной
у = 6 + 4(х+2)
у = 4х + 14
Найдем координаты точек пересечения касательной
у=4х-2 с осями координат
x=0, y =0
y =-2 x =0,5
получим точки (0;-2); (0,5 ;0)
Найдем координаты точек пересечения касательной у=4х + 14 с
осями координат
х=0 у = 0
у=14 х= -3,5
получим точки (0; 14); (-3,5; 0)
Ответ: (0; -2); (0,5; 0); (0; 14); (-3,5; 0)
№ 830 Мордкович А.Г.
На графике функции y = x3 -3x2 +4x +1 найдите точку, в которой касательная образует с положительным направлением оси абсцисс угол 450. Составьте уравнение этой касательной.
Пусть (xо;f(xо)) - точка графика функции y =x3-3x2+4x+1, в которой касательная к ее графику образует с положительным направлением оси Ox угол 45о, а y=kx+b – уравнение этой касательной, тогда k=f’(xо)=tg45о =1
Найдем f’(x) =(x3-3x2+4x+1)’ =3x2-6x+4
Получим уравнение
f’(xо) =1
3x2-6x+4 =1
3x2-6x+3 =0
x2-2x+1 =0
(x-1) 2 =0
x-1 =0
x =1
4) Составим уравнение касательной
yо = y(1) =1-3+4+1=3
y = 3+1(x-1)
y = 3+x-1
y = x+2
Ответ: xо = 1; y = x+2
Правило:
если даны две
прямые y
= k1x+b1
и y
= k2x+b2
, (k
≠ 0, k2
≠ 0), то
величина угла φ ( 0 ≤ φ ≤ ![]() )
между этими прямыми находится из
соотношений:
)
между этими прямыми находится из
соотношений:
tgφ
=![]() если k1
∙ k2
≠ -1
если k1
∙ k2
≠ -1
φ = ![]() ,
если k1
∙ k2
= -1
,
если k1
∙ k2
= -1
№ 527. Алимов Ш.А.
Под каким углом пересекаются графики функций
y = ln (1+x) и y = ln (1-x) ?
1). Найдем точки пересечения графиков
ln (1+x) = ln (1-x)
1+x = 1-x
x = 0
2) Составим уравнение касательной к y = ln (1+х) в точке хо = 0
уо = ln1 = 0
у’
=
![]()
у’о
=
![]() = 1
= 1
Получим уравнение касательной
у = 0+1(х-0)
у = х
k = 1
3) Cоставим уравнение касательной к кривой у = ln (1-x) в точке
xо = 0
уо = ln1 = 0
у’
=
![]()
у’о
=
![]() = -1
= -1
Получим уравнение касательной:
у = 0+1(х-0)
у = -х
k = -1
4) Найдем угол между касательными
k1 ∙k2 = -1
φ =
![]()
Ответ:
Задача: Прямая
у = -![]() х-
х-
![]() является касательной к линии, заданной
является касательной к линии, заданной
уравнением
у =
![]() х4
– х. Найти
координаты точек касания.
х4
– х. Найти
координаты точек касания.
Найдем точки касания
х4 – х = - х-
16х4 – 32х = -24х -3
16х4 – 8х + 3 = 0
Корнем этого уравнения является х = , проверим это по схеме Горнера
![]()



xо =
Это сложное уравнение можно заменить более простым решением. Из
условия задачи следует, что у’(xо) = - получим уравнение
∙4 xо3 -1 = -
2 xо3
=
![]()
xо3
=
![]()
xо =
3) Найдем уо
уо
=
∙![]() 4-
=
4-
=
![]() -
=
-
-
=
-
![]() = -
= -![]()
Значит точка
касания
![]()
Ответ:
Правило:
для того, чтобы прямая y = kx+b была касательной к графику функции
y = f(x), необходимо и достаточно существования хотя бы одного числа xо, для которого выполняется система
![]()
Задача: При каких значениях параметра а , прямая у = ах + 2 является
касательной к кривой у = ln х ?
Для того, чтобы прямая y = ax+2 ,была касательной к кривой y= lnx, должна выполняться система





Ответ: а=е-3
Задача. Под каким углом к оси Ох наклонена касательная к графику функции у = x2 ∙ln x в точке с абсциссой xо = 1 ?
Найдем у’
у’ = 2x ln х + х2 ∙ = 2x ln х + х
Найдем у’о = у’(1)
у’о = 2∙1∙ln 1 + 1 = 2∙0+1 =1
Найдем у’о = tg φ
tg φ = 1
φ =450
Ответ: φ =450
Задача. В каких точках угловой коэффициент касательной к графику
функции у = 2х3 – 2х2 + х – 1 равен 3?
Найдем у’
у’ = 2∙3х2 – 2∙2х + 1 = 6х2 – 4х + 1
По условию задачи у’о = 3
6xо2 - 4xо + 1 = 3
6xо2 - 4xо – 2 = 0
3xо2 - 2xо – 1 = 0
xо
= 1
xо
= -![]()
y(1) = 2 – 2 + 1 – 1 = 0
Получим точку (1:0)
y(- ) = 2∙(-
 )
– 2∙
)
– 2∙ -
- 1 = -
-
- 1 = -
 -
-
 -
-
 =
=
 = -
= -
Получим точку (- ; - )
Ответ: (1:0); (- : - )
