ТИПЫ ЗАДАЧ

НА КАСАТЕЛЬНУЮ

В ШКОЛЬНОМ КУРСЕ

АЛГЕБРЫ И НАЧАЛ АНАЛИЗА

МОУ СОШ № 10

Г. Новороссийск

Учитель математики

Волкова О.А.

Данная работа является систематизацией задач на

касательную, входящих в учебники по алгебре и началам

анализа Мордковича А.Г. и Алимова Ш.А., а так же задач,

входящих в различные сборники текстов вступительных

экзаменов в ВУЗы.

Материал может быть использован при подготовке к урокам

при систематизации знаний, а так же в качестве различных этапов

урока.

Первый тип задач на касательную

В задачах данного типа необходимо составить уравнение касательной в

точке М (x₀ ;y₀) принадлежащей графику y=f(x), т.е. М(x₀ ;y₀) –точка касания.

№823г Мордкович А.Г.

Составить уравнение касательной к графику функции

в точке х₀ = -1.

1. Уравнение касательной имеет вид

,

Где y₀ - значение функции в точке М(x₀ ;y₀)

y₀^’- значение производной в точке М(x₀ ;y₀)

2. Найдём y₀

_{y0 = y(x0) = y( -1) = 1+3+5 = 8}

3) Найдём y’

y^’ =( x² -3x +5)^’ =2x-3

y₀ ^‘ = y^’(x₀) =2∙(-1) -3 =5

4. Получим уравнение касательной:

y = 8+5(x+1)

y = 8+5x+5

y = 5x+13

Ответ: y = 5x+13

№826г Мордкович А.Г.

Составить уравнение касательной к графику функции

в точке х₀ =3

1). Уравнение касательной имеет вид:

_{y= y0 + y0}^’_(x-x0)

2).

3).

4). Получим уравнение касательной

y = 1-(x-3)

y = 1- x + 3

y = - x + 4

Ответ: y = - x + 4

Второй тип задач на касательную.

В задачах такого типа точка касания не задана явно, ее нахождение требует дополнительных рассуждений.

№828 Мордкович А.Г.

Напишите уравнение касательных к графику функции y = 9 –x² в точках его пересечения с осью абсцисс.

1). Найдём точки пересечения графика с осью абсцисс

x + 3=0 x -3 =0

x = -3 x =3

Получим две точки касания x₀ = 3 и x₀ = -3, в которых нужно составить уравнение касательной.

2). Составим уравнение касательной в точке x₀ = 3, y₀ = 0 , т.к. это точка пересечения графика с осью абсцисс

Получим уравнение касательной

3). Составим уравнение касательной в точке x₀ = -3

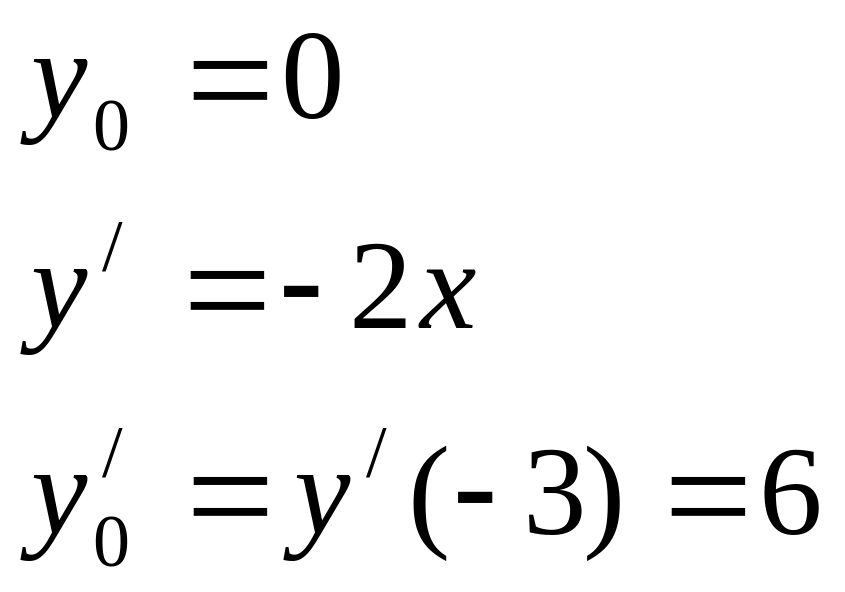
Получим уравнение касательной

Ответ:

№ 829 Мордкович А.Г.

Напишите уравнение касательных к параболе y = x² -3x в точках с ординатой 4.

1).Найдём точки касания

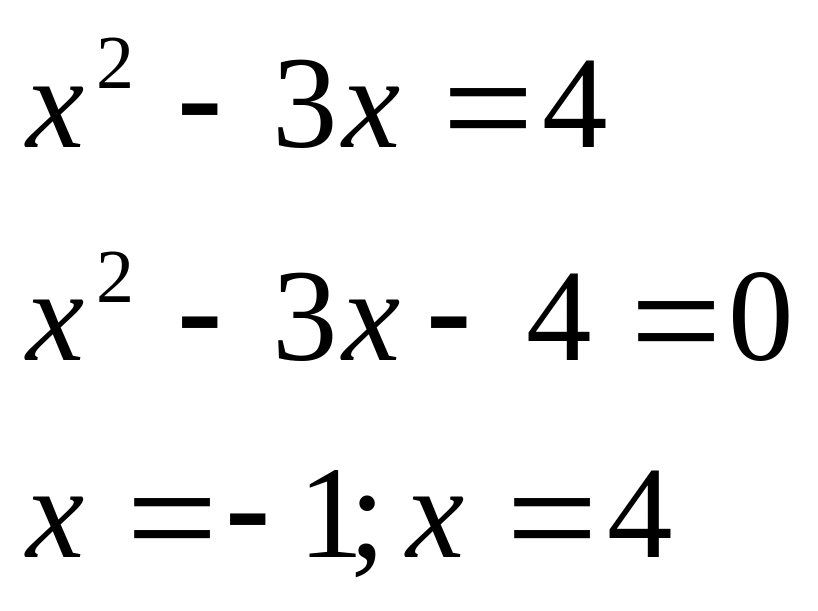
Получим две точки касания с абсциссами x₀ = -1 и x₀ = 4, в которых

нужно составить уравнение касательных.

2). Составим уравнение касательной в точке касания (-1; 4)

Получим уравнение касательной

3). Составим уравнение касательной в точке касания (4; 4)

Получим уравнение касательной

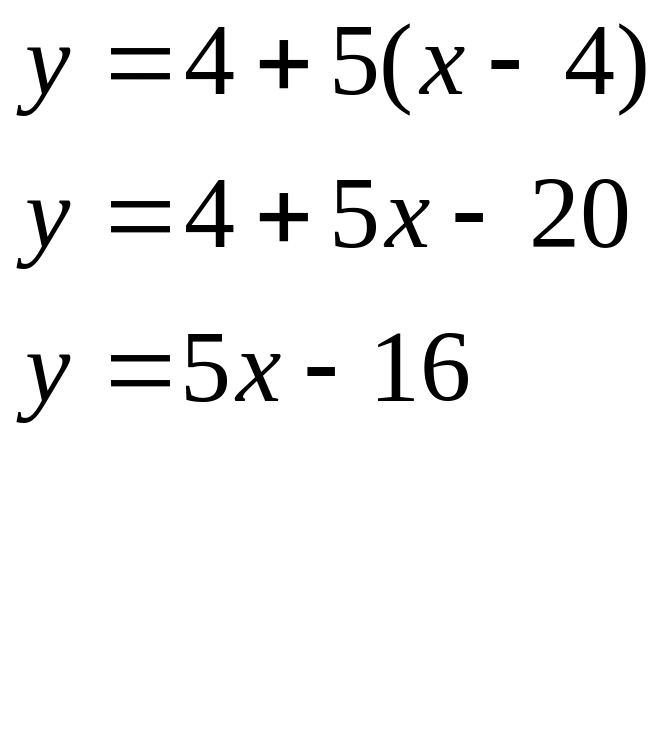
Ответ: