21) Уравнение Шредингера для частицы вблизи потенциального барьера прямоугольной формы.

С тационарные уравнения Шредингера имеют вид:

где , – волновые вектора, – постоянная Планка. Решение волнового уравнения при ищем в виде суммы падающей и отражённой волны , а решение при – в виде прошедшей волны . решение в области потенциального барьера  есть . Постоянные коэффициенты a, b, c, d определяются из условия непрерывности волновой функции и в точках  и .

В качестве коэффициента прозрачности барьера D естественно взять отношение плотности потока вероятности прошедших частиц к плотности потока вероятности частиц, падающих на барьер. В рассматриваемом случае, это отношение будет просто равно квадрату модуля волновой функции, оказавшейся за барьером, так как амплитуда падающей волны принята за единицу, а волновые вектора падающей и прошедшей волны совпадают.

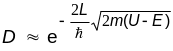
Как видно из полученного соотношения, вероятность прохождения тем больше, чем уже барьер (меньше L) и чем он ниже (меньше разность U - E).

2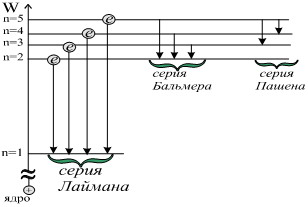 2) Квантовый гармонический осциллятор - это колеблющаяся по гармоническому закону микрочастица, находящаяся в связанном состоянии внутри атома или ядра.

потенциальная энергия .

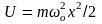стационарное уравнение Шредингера

приобретает вид:

.

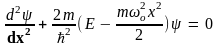Спектр собственных значений энергий:

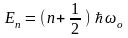
,где квантовое число n = 0, 1, 2, 3 ... . Таким образом, существует и "нулевая энергия"

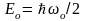
Существование отличной от нуля минимально возможной энергии осциллятора имеет глубокий смысл. Это означает, что колебания микрочастиц не прекращаются никогда, что в свою очередь означает недостижимость абсолютного нуля температуры.

23) Боровская теория атома водорода

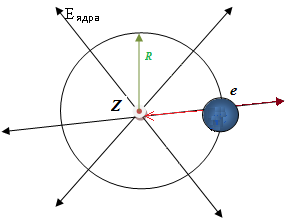Электроны притягиваются к ядру за счет электростатических сил взаимодействия. Однако электроны не падают на ядро, поскольку вращаются вокруг него с определенной скоростью, т.е. имеют определенную кинетическую энергию.

Электрон находится на определенном расстоянии от ядра, так как обе силы -  центростремительная F_цс, связывающая заряженные частицы, и центробежная F_цб, стремящаяся оторвать электрон от ядра, - уравновешивают друг друга, т.е. 

F_цс = F_цб.

Постулаты Бора — основные допущения для объяснения закономерности линейчатого спектра атома водорода и водородоподобных ионов и квантового характера испускания и поглощения света.

Первый постулат Бора (постулат стационарных состояний): электроны в атоме могут обладать лишь определенными (разрешенными) значениями энергии, другими словами-находиться на определенных энергетических уровнях, образующих дискретный энергетический спектр атома.

Второй постулат Бора (правило частот): при определенных условиях электроны могут переходить с одного уровня на другой (или с одной орбиты на другую), поглощая или испуская фотон.Существует орбита с наименьшей возможной энергией, на которой электрон может находиться неограниченно долго

это его основное состояние. При переходе с низшего энергети ческого уровня на высший электрон возбуждается, но при каждом удобном случае всегда стремиться вернуться из возбужденного состояния обратно в основное.

Правило квантования орбит: из всех орбит электрона возможны только те, для которых момент импульса равен целому кратному постоянной Планка

Уравнение движения электрона по круговой орбите:

Серия Бальмера — спектральная серия в спектре атома водорода.

Данная серия образуется при переходах электронов с возбужденных энергетических уровней на второй в спектре излучения и со второго уровня на все вышележащие уровни при поглощении.

Ф ормула Бальмера

Где n — главное квантовое число — натуральное число, большее или равное 3.

Достоинства теории Бора

1)Объяснила дискретность энергетических состояний водородоподобных атомов.

2)Теория Бора подошла к объяснению внутриатомных процессов с принципиально новых позиций, стала первой полуквантовой теорией атома.

3)Эвристическое значение теории Бора состоит в смелом предположении о существовании стационарных состояний и скачкообразных переходов между ними. Эти положения позднее были распространены и на другие микросистемы.

Недостатки теории Бора

1)Не смогла объяснить интенсивность спектральных линий.

2 )Справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева.

3)Теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно — уравнение движения электрона — классическое, другое — уравнение квантования орбит — квантовое.

24) уравнение Шредингера для атома водорода

Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, где , h — постоянная Планка, E — полная энергия электрона, — оператор Лапласа.

И уравнение Шредингера в сферических координатах:

Пространственное квантование -квантование не только вектора, но и его проекции. Оно приводит к «расщеплению» энергетических уровней на ряд подуровней.

Вырождение энергетических уровней, существование двух или более стационарных состояний квантовой системы (атома, молекулы) с одинаковыми значениями энергии. С истема, полная энергия которой определяется заданием оператора Я (гамильтониана), может иметь т стационарных состояний, для которых ур-ние Шрёдингера определяет соответствующие волновые ф-ции (i = 1, 2, ..., т)и одно значение энергии Е, одинаковое для всех т состояний. Энергетич. уровень с энергией Е при наз. вырожденным, число т разл. независимых волновых ф-ций - кратностью вырождения уровня. О состояниях с волновыми ф-циями говорят как о состояниях, вырожденных по энергии, или вырожденных состояниях. Если одному значению энергии отвечает одно состояние, т.е. m=1, уровень наз. невырожденным.