Энтропия по Больцману

где константа k = 1,38×10⁻²³ Дж/К постоянная Больцмана, а Ω — статистический вес состояния, является числом возможных микросостояний (способов) с помощью которых можно перейти в данное макроскопическое состояние.

6) Предположим, что на N одинаковых микрочастиц приходится G различных состояний, в которых может находиться отдельная микрочастица. Мерой частоты «встреч» микрочастиц может служить отношение N/G. Микрочастицы будут встречаться редко, если выполнено следующее условие: N/G<<1

В этом случае число различных вакантных состояний много больше числа микрочастиц. Подобные коллективы называются невырожденными, условие N/G<<1 называют условием невырожденности.

Если число состояний G оказывается одного порядка с числом частиц N, то вопрос о том, как заселять состояния — поодиночке или коллективно, становится весьма актуальным. В этом случае специфика фермионов и бозонов проявляется в полной мере, оказывая значительное влияние на свойства коллектива как целого. Такие колективы называются вырожденными. Вырожденные коллективы могут образовываться только квантово-механическими объектами.

Р аспределение Максвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию, также применимо для электронных процессов переноса и к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Так, мы получили - функцию плотности вероятности, которая и называется распределением Максвелла.

н аиболее вероятная скорость, — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению . Чтобы найти её, необходимо вычислить , приравнять её нулю и решить относительно :

Среднеарифметическую:

7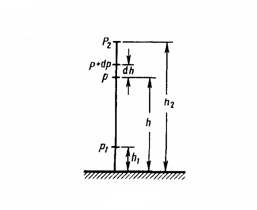 ) Барометрическая формула. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту Если температура не зависит от высоты, то давление газа меняется с высотой по закону: ,

где  — высота,  — молярная газовая постоянная,  — постоянная Больцмана,  — ускорение свободного падения вблизи поверхности земли,  — молярная масса газа,  — масса одной молекулы,  — абсолютная температура.

Поделив барометрическую формулу на , с учетом уравнения состояния идеального газа, получим распределение Больцмана — зависимость концентрации молекул от потенциальной энергии: , где  — потенциальная энергия молекулы. В однородном поле силы тяжести .

График температур сканировать