7.1. Ентропія

Як уже вказувалося, теплота q не є функцією стану, і dq = du + pdv не буде повним диференціалом; dq являє собою тільки деяку нескінченно малу величину. Для того щоб проінтегрувати праву частину рівняння першого закону термодинаміки dq= du + pdv, повинна бути відома залежність р від v (або р від Т). У математиці доводиться, що диференційний двочлен завжди можна перетворити в повний диференціал шляхом ділення (або множення) на інтегруючий дільник. Таким інтегруючим дільником для елементарної кількості теплоти dq є абсолютна температура Тº К.

Покажемо це на прикладі ідеального газу. Маємо dq = c_v dT + pdv, або, замінивши р на RT/v, получимо dq = c_v dT + RTdv/v.

Розділивши обидві частини останнього рівняння на Т, знаходимо

dq/T =c_v dT/T + Rdv/v, ( 6-38)

Звідси вираження dq/T при оборотній зміні стану газу є повний диференціал деякої функції змінних Т и v (с_v залежить тільки від температури, а R — величина постійна). Клаузиус назвав цю функцію ентропією й позначив буквою S. Виміряється повна ентропія S у джоулях на градус (дж/град), а питома ентропія s — у джоулях на кілограм на градус (дж/( кг-град)).

Таким чином, диференціал ентропії для оборотної зміни стану визначається як

ds = dq/T, ( 6-39)

Ентропія є однозначна функція стану газу, що приймає для кожного його стану цілком певне значення. Ентропія є екстенсивним (залежить від маси ре-

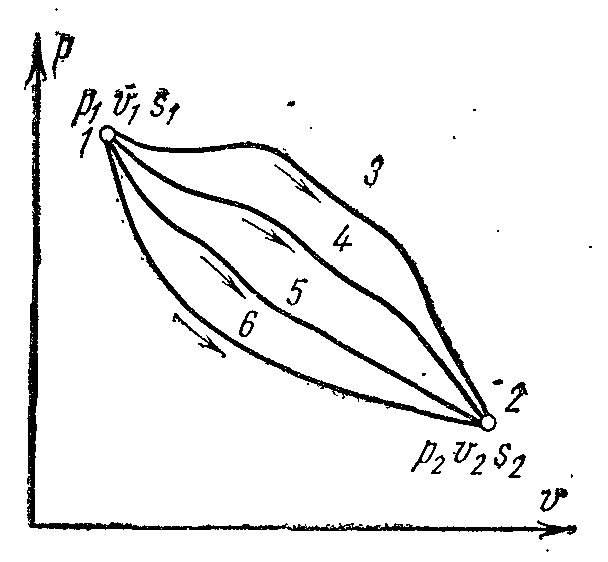
човини) параметром стану й зміна її в будь-якому термодинамічному процесі повністю визначається крайніми станами тіла й не залежить від шляху процесу. У зв'язку із цим ентропія газу, будучи параметром стану, у процесах 1-3-2, 1-4-2, 1-5-2, 1-6-2 (мал. 6-1) буде змінюватися однаково. Ця властивість відноситься як до оборотних, так і необоротних процесах. Тому

Оскільки ентропія має властивість адитивності, то алгебраїчна сума змін ентропії окремих тіл, що складають термодинамічну систему, буде дорівнювати зміні ентропії всієї термодинамічної системи в цілому. Причому зміни ентропії окремих тіл залежно від процесу можуть бути як позитивними, так і негативними величинами.

Ентропія може бути визначена як функція основних параметрів стану:

Повні диференціали ентропії мають вигляд:

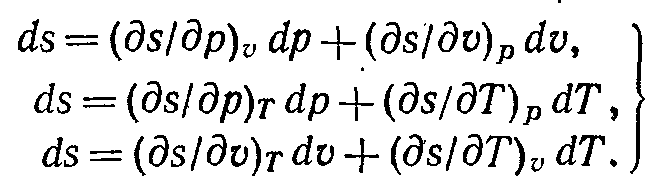(6-40)

Частинні похідні ентропії, що входять у ці рівняння, обчислюються за рівняннями, які виведені в гл. X.

Для одержання зміни ентропії як функції Т і v співвідношення (6-38) представимо в наступному виді:

^(6-41)

Інтегруючи, при с_v = const знайдемо для ідеального газу

^(6-42)

Для одержання зміни ентропії як функції Т і р слід з рівняння (6-41) виключити v. З рівняння Клапейрона після диференціювання одержимо:

Підставляючи значення dv/v у рівняння (6-41), маємо

Інтегруючи при c_p = const, знаходимо

^(6-43)

Для одержання зміни ентропії як функції р і v треба з рівняння (6-41) виключити Т. Користуючись тим же методом, одержимо

звідки

Інтегруючи, визначаємо

(6-44)

З огляду на те, що зміна ентропії тіла не залежить від характеру процесу, отримані рівняння (6-42), (6-43) і (6-44) застосовні як для оборотних, так і для необоротних процесів.

З рівняння (6-39) можна одержати загальну формулу для визначення теплоємності.

Теплоємність с_х будь-якого процесу дорівнює добутку абсолютної температури Т на частинну похідну ентропії s по температурі Т при х = const:

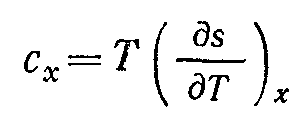( 6-45)

Підставивши в рівняння (5-9) і (5-13) значення dq з рівняння (6-39), одержимо

^(6-46)

^(6-47)

Рівності (6-46) і (6-47) містять тільки параметри стану і їхні диференціали й носять назву термодинамічних тотожностей; вони відносяться до оборотних процесів.

Якщо в термодинамічній системі крім роботи зміни об'єму відбувається робота dl_v, не пов'язана зі зміною об'єму тіла, то термодинамічні тотожності мають вигляд

^{( 6-48)}

^{( 6-49)}

У термодинаміку внутрішня енергія, ентальпія, ентропія, теплоємності називаються калоричними властивостями речовини, а питомий об'єм, абсолютний тиск, температура — термічними властивостями.