5.5. Перше начало термодинаміки

Нехай 1 кг робочого тіла здійснює деякий процес (мал. 5-10), на елементарній ділянці якого а-b підводять нескінченно малу кількість енергії у формі теплоти, при цьому температура й об'єм тіла збільшуються відповідно на нескінченно малі величини dТ і dv.

З підвищенням температури тіла на dТ збільшується швидкість молекул або збільшується його внутрішня кінетична енергія. Зі збільшенням об'єму тіла на dv збільшується відстань між молекулами, що пов'язане зі збільшенням його внутрішньої потенційної енергії.

Сума змін внутрішньої, кінетичної й внутрішньої потенційної енергії представляє повну зміну внутрішньої енергії dи. Зі збільшенням об'єму на dv тіло здійснює зовнішню роботу з подолання зовнішніх сил, що позначають dl. Якщо, у робочому тілі не відбувається яких-небудь інших явищ і відсутня кінетична енергія видимого руху, то, відповідно до закону збереження енергії, можна написати для елементарного процесу з урахуванням обраного правила знаків наступне

рівняння:

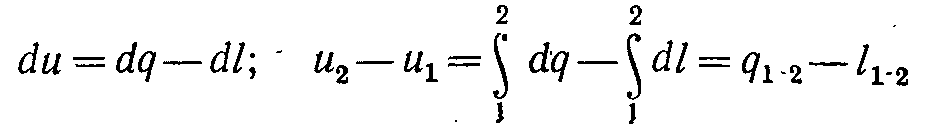( 5-8)

або для оборотних процесів

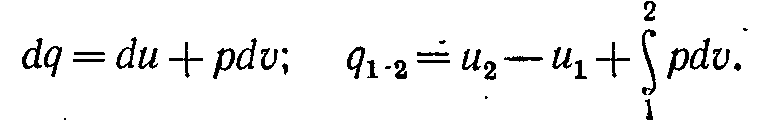(5.9)

Отримане рівняння є математичним (аналітичним) вираженням першого закону термодинаміки. Воно формулюється так: зміна внутрішньої енергії термодинамічної системи дорівнює алгебраїчній сумі отриманою системою енергії у формі теплоти dq і виконаної нею зовнішньою роботою dl, або підведена до робочого тіла енергія у формі теплоти витрачається на зміну внутрішньої енергії тіла й на здійснення тілом зовнішньої роботи.

Основне рівняння першого закону термодинаміки ( 5-9) як закону збереження енергії було отримано для процесів, у яких не відбувається переміщення робочого тіла в просторі. В останньому випадку в основне рівняння необхідно ввести додатковий доданок _, що враховує приріст кінетичної енергії 1 кг газу при його переміщенні в просторі на ділянці розглянутого процесу. Тоді рівняння першого закону термодинаміки приймає вид

^{( 5-10)}

де dl' — робота газу проти зовнішніх сил при його русі, або робота проштовхування (вона не дорівнює роботі розширення dl); — приріст зовнішньої кінетичної енергії газу при його переміщенні, називане роботою, що є у розпорядженні.

Отримане рівняння першого закону термодинаміки ( 5-8) справедливо для будь-яких робочих тіл і, зокрема, для ідеальних газів. Це рівняння описує як оборотні, так і необоротні процеси. Дійсно, для необоротних процесів

, ( 5-11)

де dq_Tp — теплота тертя; dl_Tp — робота проти сил тертя. Але оскільки робота, витрачена на подолання сил тертя, переходить повністю в теплоту тертя, то dq_TР = dl_TP. Отже, рівняння ( 5-8) описує й необоротні процеси.

Всі величини, що входять у рівняння( 5-8), можуть бути як позитивними, так і негативними й у деяких випадках можуть приймати нульові значення.

5.6. Ентальпія.

Якщо за незалежні параметри вибрати тиск р і температуру Т, то можна одержати для оборотних процесів інший вид аналітичного вираження першого закону термодинаміки:

dq = du + pdv = dp + d (pv) - vdp = d (u + pv) - vdp.

Як бачимо, тут з'явилася нова функція:

^{, (5.12)}

яку назвали ентальпією.

Тоді dq = di — vdp , ( 5-13)

а 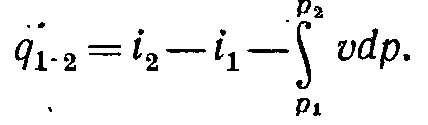( 5-14)

Абсолютне значення ентальпії термодинамічної системи можна одержати, проінтегрував рівняння ( 5-13). У результаті інтегрування у вираження для i увійде постійна інтегрування i₀:

^{( 5-15)}

тобто ентальпія системи визначається з точністю до деякої адитивної постійної i₀. Цю постійну вибирають довільно, і в більшості випадків ентальпію ідеального газу (при р 0) уважають рівної нулю при 0° С, а константу інтегрування не враховують.

Якщо в термодинамічній системі протікають оборотні процеси й поряд з роботою зміни об'єму pdv виконується робота, не пов'язана зі зміною об'єму системи, яка віддається зовнішньому об'єкту, то в праві частини рівнянь ( 5-9) і ( 5-13) увійде додатковий член l_v:

^{( 5-16)}

^{( 5-17)}

Рівняння ( 5-16) і ( 5-17) є найбільш загальним аналітичним вираженням першого закону термодинаміки для оборотних процесів зміни стану термодинамічної системи.

При р = const рівняння ( 5-13) перетворюється в

dq_p = di. ( 5-18)

Диференціал ентальпії di є елементарна кількість теплоти, що беруть участь у процесі при постійному тиску. Вся теплота в процесі при постійному тиску витрачається на зміну ентальпії:

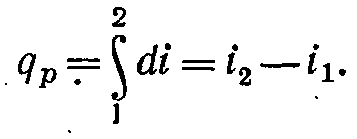(5.19)

З рівняння ( 5-13) слідує, що

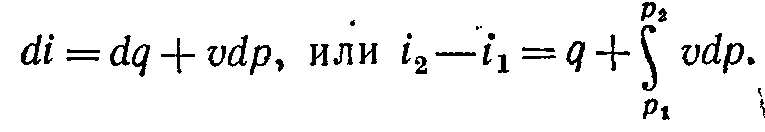( 5-20)

Ентальпія більше зовнішньої теплоти на величину робота vdp, що на рv-діаграмі зображується елементарною площадкою abed (мал. 5-11),

Зміна ентальпії повністю визначається початковим і кінцевим станами робочого тіла й не залежить від проміжних станів. Зміна ентальпії газу в циклах дорівнює нулю, тобто,

Оскільки ентальпія є функцією основних параметрів стану, то di є повний диференціал цієї функції при будь-яких незалежних змінних, що характеризують стан газу:

звідки

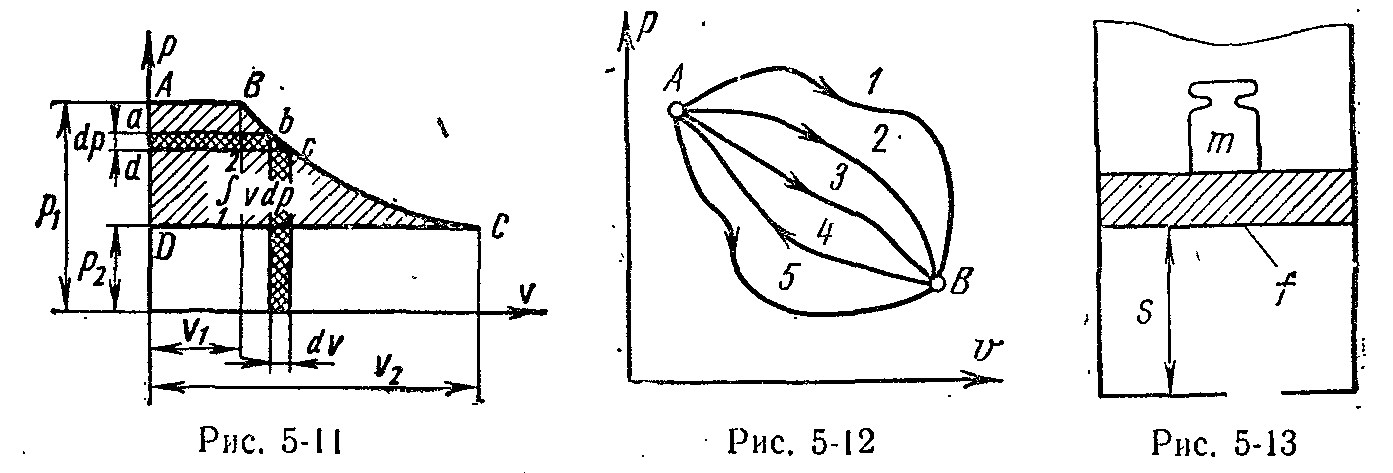
Зміна ентальпії у всіх процесах, що протікають між двома точками А та В, однакова (мал. 5-12). Фізичний зміст ентальпії буде зрозумілий з розгляду наступного приклада. На поршень, що переміщається, у циліндрі з 1 кг газу поміщена гиря масою m кг (мал. 5-13). Площа поршня f, внутрішня енергія робочого тіла u. Потенційна енергія гирі дорівнює добутку маси гирі m на висоту S. Оскільки тиск газу р урівноважується масою гирі, то потенційну енергію її можна виразити так:

Добуток fS є питомий об'єм газу. Звідси

Добуток тиску на об'єм є робота, яку треба затратити, щоб увести газ об'ємом v у зовнішнє середовище з тиском р. Таким чином, робота pv є потенційна енергія газу, що залежить від сил, що діють на поршень. Чим більше ці зовнішні сили, тим більше тиск р і тем більше потенційна енергія тиску pv.

Якщо розглядати газ, що перебуває в циліндрі, і поршень із вантажем як одну систему, що будемо називати розширеною системою, то повна енергія Е цієї системи складається із внутрішньої енергії газу u і потенційної енергії поршня з вантажем, рівної pv:

Звідси видно, що ентальпія i дорівнює енергії розширеної системи — тіла й навколишнього середовища. У цьому й полягає фізичний зміст ентальпії.

Значення ентальпії для пар, газів, газових сумішей приводяться в технічній і довідковій літературі. Користуючись цими даними, можна визначати кількість теплоти, що бере участь у процесі при постійному тиску. Ентальпія має велике значення й застосування при розрахунках теплових і холодильних установок і як параметр стану робочого тіла значно спрощує теплові розрахунки. Вона дозволяє застосовувати графічні методи при дослідженні всіляких термодинамічних процесів і циклів.

Ентальпією особливо доцільно користуватися тоді, коли як основні параметри приймають р і Т. Це наочно можна бачити, якщо ентальпію i зрівняти із внутрішньою енергією и. При v = const рівняння першого закону термодинаміки перетворюється в dq_v = du, або q_v = u₂ — u₁, а при р = const q_р = i₂ – i₁.

Ентальпія ідеального газу, так само, як і внутрішня енергія, є функцією температури й не залежить від інших параметрів. Дійсно, для ідеального газу

отже (оскільки обоє доданків залежать тільки від температури),

i = f (Т).

Тоді за аналогією із внутрішньою енергією маємо

(di/dТ)_p = (di/dТ)_v = di/dТ,

тобто у будь-якому процесі зміни стану ідеального газу похідна від зміни ентальпії по температурі буде повною похідною.