14.1. Максимальна робота й функції стану.

Внутрішня енергія тіла U, його ентальпія I та ентропія S є функціями стану; тому й будь-яка їхня комбінація з термічними параметрами р, V, Т буде являти собою функцію станів тіла. Із усіх цих комбінацій особливе значення мають ті, за допомогою яких найбільше просто виражається робота, вироблена тілом при зміні його стану.

Максимальна робота. Максимальна корисна зовнішня робота L'_max являє собою роботу, що провадить система над зовнішнім теплоізольованим об'єктом роботи в оборотному процесі 1—2. Роботу, що повинно затратити зовнішнє джерело роботи, щоб повернути систему зі стану 2 у вихідний стан 1 у тих же самих умовах, тобто роботу зворотного оборотного процесу 2—1, називають мінімальною роботою; при цьому L'_max = – L'_min.

У самому загальному випадку L'_max складається із двох частин: роботи, пов'язаної зі зміною об'єму, і роботи L_(V), не пов'язаної зі зміною об'єму.

Надалі розглядаються наступні два випадки: 1) робота виробляється одиночним однорідним тілом при наявності джерел тепла різної температури; 2) робота виробляється тілом, що перебуває в навколишньому середовищі, тиск р' і температура Т' якого незмінні.

1.1. Максимальна робота тіла. Зовнішній об'єкт роботи (джерело роботи), передбачається теплоізольованим від тіла, внаслідок чого взаємодія між тілом і джерелом роботи має винятково механічний характер: у кожній точці оборотного процесу джерело роботи здійснює на тіло тиск, у точності рівний тиску тіла.

Знайдемо вираження для максимальної роботи, чиненої тілом при переході з початкового стану 1 у кінцевий стан 2 в умовах, коли один з термодинамічних параметрів зберігає незмінне значення.

1.1.1. Розглянемо спочатку оборотний ізоентропічний процес зміни стану тіла, що характеризується сталістю ентропії тіла: S = const.

У цьому випадку з першого та другого начал термодинаміки

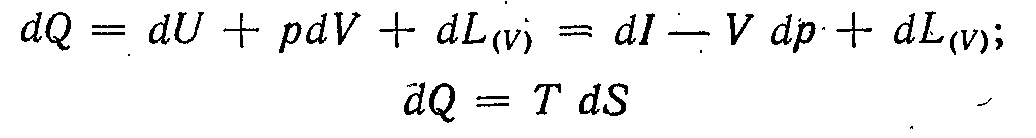
або, що те ж саме, з термодинамічної тотожності

слідує

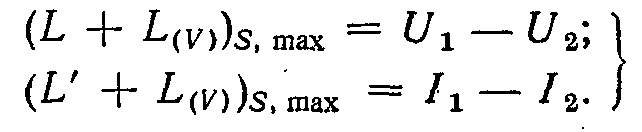( 3-1)

При L_(V) = 0

Таким чином, при ізоентропічному процесі максимальна робота зміни об'єму дорівнює втраті внутрішньої енергії, а максимальна корисна зовнішня робота, пов'язана зі зміною об'єму, дорівнює втраті ентальпії.

1.1.2. Визначимо тепер максимальну роботу, здійснену при ізотермічному процесі, тобто при Т = const. Зважаючи на те, що в оборотному процесі як початковий, так і кінцевий стан, є рівноважними й характеризуються тим самим значенням температури, для здійснення такого процесу може бути використане джерело теплоти тієї ж температури, що й температура тіла в початковому стані.

Складемо з U, S, Т наступне вираження:

F = U — TS. (3.2)

Функцію стану F називають енергією Гельмгольца (раніше вона називалася вільною енергією).

Неважко переконатися, що зменшення цієї функції, тобто різниця F₁ — F₂, чисельно дорівнює максимальній роботі зміни об'єму, чиненої тілом при оборотному ізотермічному переході з початкового стану 1 у кінцевий стан 2. Дійсно, відповідно до першого початку термодинаміки

але внаслідок оборотності процесу й сталості температури тіла

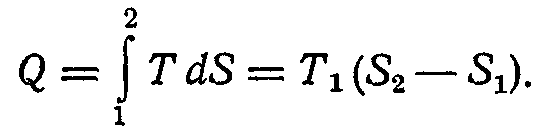^{( 3-А)}

Таким чином,

або

^(3.3)

Визначимо максимальну корисну зовнішню роботу, що може бути здійснена тілом над зовнішнім об'єктом роботи при оборотному ізотермічному процесі.

Оскільки відповідно до першого начала термодинаміки

а при оборотному ізотермічному процесі Q береться з ( 3-А), то

Величину I – TS, що представляє собою функцію стану, називають енергією Гиббса (ізобарним потенціалом) і позначають через Ф:

^(3.4)

Як ми тільки що переконалися,

^(3.5)

тобто максимальна корисна зовнішня робота при ізотермічному процесі дорівнює втраті енергії Гіббса.

1.2. Максимальна робота, вироблена тілом, що перебуває в навколишнім середовищі. Якщо тіло перебуває в навколишнім середовищі, температура й тиск якої постійні й є рівними Т', р', то корисна зовнішня робота, що може бути зроблена тілом у процесі 1—2 над зовнішнім об'єктом роботи, відповідно до рівняння (2.96) становить

де U, S, V — відповідно внутрішня енергія, ентропія й об'єм тіла;

U* = U + V, S* = S+ S', V* = V + V' - відповідно внутрішня енергія, ентропія й об'єм всієї системи в цілому, тобто тіла й навколишнього середовища.

Максимальна робота L'_max виробляється тілом при оборотному проведенні процесу 1—2, коли ∆S* = 0; вона дорівнює взятої зі зворотним знаком мінімальній роботі L'_min , тобто

^(3.6)

При цьому передбачається, що вся робота над зовнішнім об'єктом (джерелом) роботи виробляється тільки тілом; навколишнє середовище із зовнішнім джерелом роботи не взаємодіє й зовнішньої корисної роботи не робить. Відповідно до цього при оборотній зміні стану навколишнього середовища на підставі термодинамічної тотожності маємо

Оскільки при ∆S* = 0 зміна ентропії навколишнього середовища й тіла пов'язані співвідношенням а за умовою сталості об'єму всієї системи в цілому то це співвідношення може бути переписане у вигляді

^(3.7)

1.3. Визначимо тепер корисну зовнішню роботу, вироблену адіабатно ізольованою системою, що складає тіло разом з навколишнім середовищем.

Ізольована система має постійний об'єм, тому вся вироблена нею корисна зовнішня робота не пов'язана зі зміною об'єму.

Оборотна зміна стану складної ізольованої системи означає наступне. Ізольована система складається в самому загальному випадку з окремих частин, що відрізняються одна від другої (наприклад, по температурі, тиску, сполуці й т.д.), і які в загальному випадку можуть бути навіть не зв'язані між собою. Ентропія, внутрішня енергія й об'єм системи в цілому дорівнюють відповідно сумі ентропії, внутрішніх енергій і об'ємів частин, що становлять систему. Коли температура, тиск, склад або які-небудь інші властивості різних частин системи відрізняються, то стан системи не є, природно, станом повної термодинамічної рівноваги й повинен підтримуватися дією різних регуляторів: адіабатичних перегородок, твердих стінок, напівпроникних перегородок і т.д. Якщо дія регуляторів здійснюється досить повільно, тобто квазістатично, так щоб у будь-який момент часу кожна із частин системи перебувала в локальній рівновазі, а загальна ентропія й об'єм системи зберігали незмінні значення, то стан системи буде змінюватися оборотним образом.

Підставивши в рівняння (3-6) значення

що є рівним, як було показано вище, переконуємося, що максимальна корисна зовнішня робота адіабатично ізольованої системи дорівнює втраті внутрішньої енергії системи

^(3.8)

Величина являє собою максимальну корисну зовнішню роботу адіабатно ізольованої системи при оборотній зміні її стану коли об'єм V* і ентропія S* системи зберігають незмінне значення.

1.4.-1.4.1. З термодинамічної тотожності можна одержати також вираження для максимальної корисної зовнішньої роботи в тому випадку, коли при оборотній зміні стану системи не міняються величини V* і U*

^(3.9)

1.4.2. Знайдемо тепер роботу, вироблену тілом при ізоентропічному процесі. Якщо стан тіла, що перебуває в навколишнім середовищі, змінюється ізоентропічно, то S₂ + S₁, і тому відповідно до рівняння (3.6) максимальна корисна зовнішня робота

^(3.10)

1.4.3. Якщо тиск тіла при ізоентропічному процесі не міняється й дорівнює тиску навколишнього середовища, тобто р = р', то на підставі вираження ( 3-10)

^(3.11)

Вираження (3.11) зберігає свою силу й у тому випадку, якщо тиск тіла в початковому й кінцевому станах дорівнює тиску навколишнього середовища а в проміжних станах р ≠ р', тобто тіло в початковому й кінцевому станах перебуває в рівновазі з навколишнім середовищем, а в проміжних станах рівновага між тілом і середовищем відсутній.

Оскільки тіло разом з навколишнім середовищем являють собою адіабатно ізольовану систему, то рівняння (3.11) визначає також корисну зовнішню роботу адіабатно ізольованої системи за умови S = const, p'= const.

1.5. Обчислимо, далі, роботу, вироблену тілом в ізотермічному процесі, коли температура тіла дорівнює температурі навколишнього середовища, тобто Т = Т'. Якщо до того ж об'єм тіла не міняється, тобто V = const, то відповідно до вираження (3.6)

^{( 3-12)}

Ясно, що при V = const корисна зовнішня робота не пов'язана зі зміною об'єму тіла, тобто дорівнює L_(V).

Вираження (3.12) справедливо й у тому випадку, коли в проміжних станах Т ≠ Т ' і V ≠ const, але в кінцевому й початковому станах Т ₂ = Т ₁ = Т ', V₂= V₁ .

Якщо тиск тіла незмінний, а температура тіла дорівнює температурі навколишнього середовища (або якщо в початковому й кінцевому станах Т ₁ = Т ₂ = Т ', р₁ = р₂ = р' ) , то

^(3.13)