9.3. Ізобарний процес

При ізобарному процесі виконується умова dp = 0 або р = const.

Такий термодинамічний процес може протікати в циліндрі, поршень якого переміщається без тертя так, що тиск у циліндрі дорівнює постійному тиску навколишнього середовища, що діє на поршень іззовні (мал. 7-4, а).

Рівняння ізобарного процесу може бути отримане з рівняння стану ідеального газу при р = const. У цьому випадку

^{( 7-5)}

Таким чином, при ізобарному процесі (постійному тиску) об'єм тієй самої кількості газу завжди пропорційний абсолютній температурі.

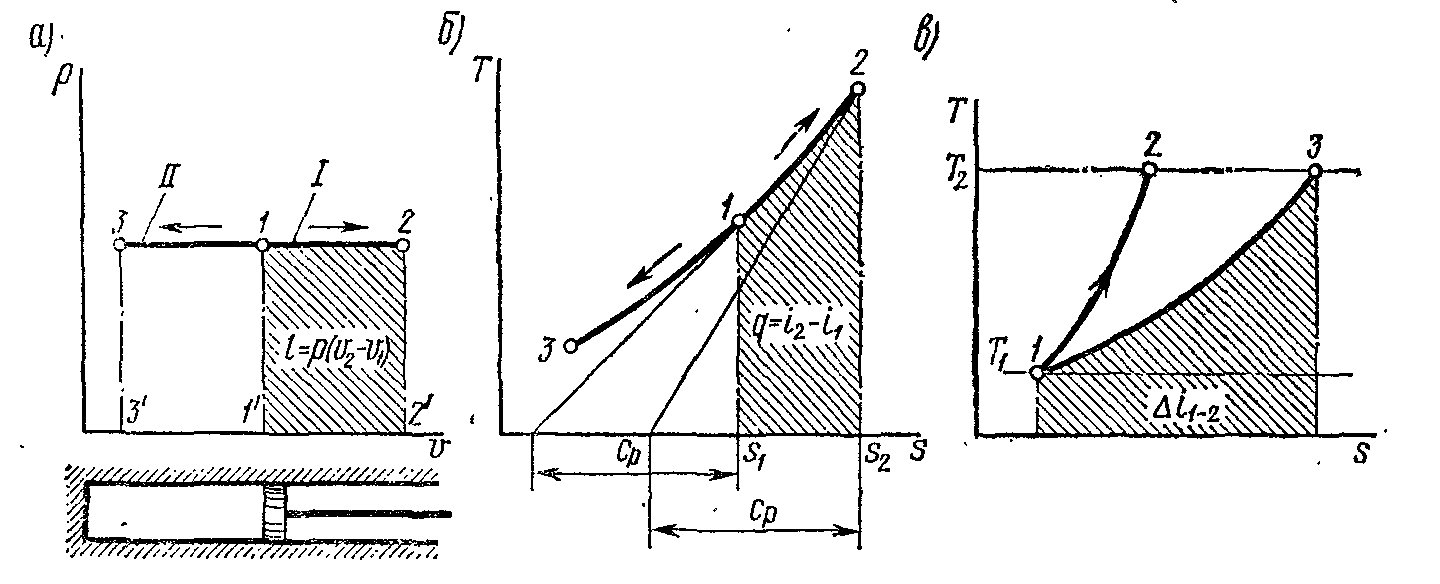
Рис. 7-4, а – в

На мал. 7-4, а зображений графік процесу. Крива процесу називається ізобарою.

Це співвідношення називається законом Гей-Люссака.

При розширенні газу його температура зростає, при стисненні - зменшується.

Питома робота зміни об'єму при цьому виражається наступним рівнянням:

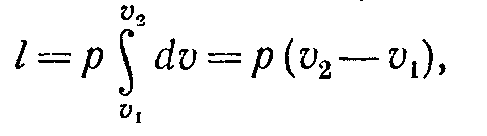( 7-6)

або з урахуванням того, що p v₁ = RT₁, і pv₂ = RT₂, , ( 7-6')

тобто робота газу при ізобарному процесі позитивна тільки в тому випадку, якщо температура газу збільшується.

Корисна зовнішня робота при цьому (робота, що є у розпорядженні)

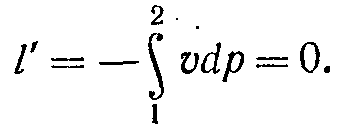
На vp-діаграмі робота газу зображується у вигляді пл. 11'22' під процесом 1-2 (рис. 7-4, а), причому l > 0, якщо v₂ > v₁.

Поклавши у формулі ( 7-6') T₂ - T₁ = 1º, знайдемо l = R. Отже, питома газова постійна - це робота 1 кг газу в ізобарному процесі при збільшенні температури на 1º.

При відомому значенні істинної питомої теплоємності ізобарного процесу с_p питома теплота q, що підводиться до робочого тіла (або що відводиться), при dp = 0 визначається рівнянням

звідки

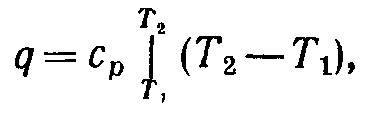
де с_p |^T_2T1 — середня ізобарна теплоємність в інтервалі температур від T₁ до Т₂.

Якщо с_p = const, то

^{( 7-7)}

Із цього співвідношення видно, що теплота, підведена до робочого тіла в ізобарному процесі, йде на збільшення його ентальпії.

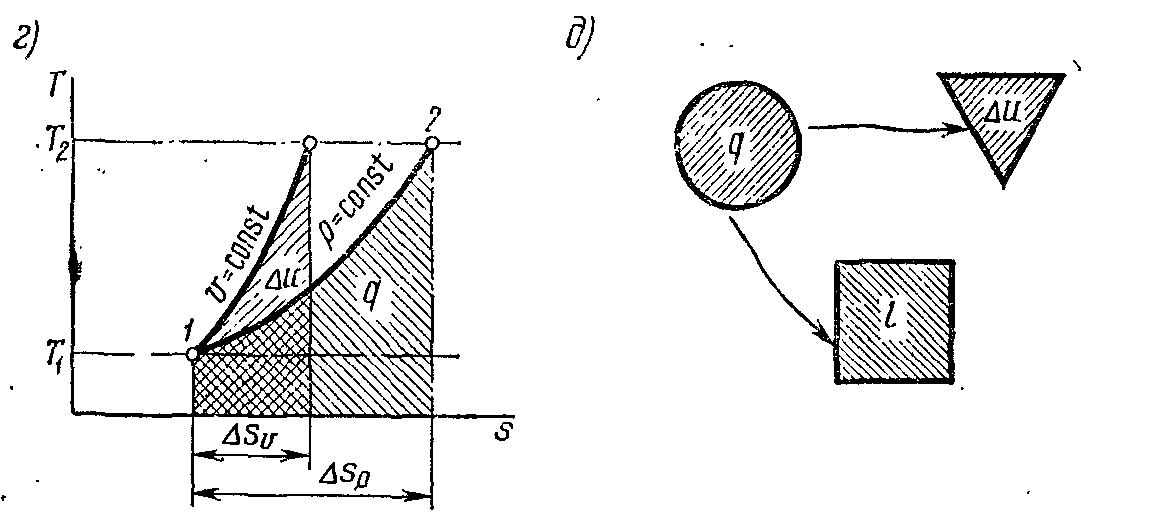
Рис. 7-4, г – д

При ізобарному процесі міняється температура робочого тіла отже, і його внутрішня енергія.

Тому на здійснення зовнішньої роботи витрачається лише частина наданої тілу ззовні теплоти q_{p, 1-2} , яка дорівнює р(v₂ – v₁), а інша частина йде на збільшення внутрішньої енергії тіла. Перетворення енергії при ізобарному розширенні газу ілюструється схемою на мал. 7-4, д

Для визначення частки теплоти, затрачуваної в ізобарному процесі на зовнішню роботу, треба всі члени рівняння першого закону термодинаміки розділити на dq:

1 = du/dq + dl/dq,

звідки з урахуванням співвідношення k = γ = c_p/c_v

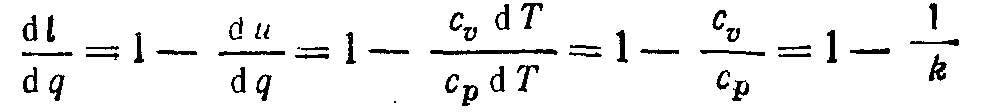
и

d u/dq = 1/k.

Якщо прийняти k = 1,4, що відповідає двохатомним газам, то

dl/dq = 0,285 і du/dq = 0,715.

Отже, 28,5% всієї підведеної до робочого тіла теплоти в ізобарному процесі двохатомного газу витрачається на здійснення зовнішньої роботи, а 71,5% - на зміну внутрішньої енергії.

Для оборотного ізобарного процесу при постійній теплоємності зміна ентропії знаходиться з рівняння ( 6-43):

але при р = const ln p₂/p₁ = 0, тому

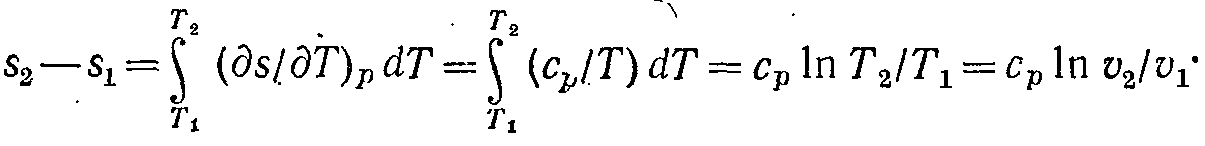( 7-8)

Таким чином, ізобара на sТ-діаграмі є деякою логарифмічною кривою (див. рис. 7-4,б) і, подібно ізохорі, звернена опуклістю долілиць.

Якщо Т₂ > T₁ то відповідно до вираження (7-8) ∆s_p = s₂ – s₁ > 0, тобто ізобарний процес на sТ-діаграмі (рис. 7-4, б) протікає так, що при збільшенні ентропії збільшується й температура. Якщо провести міркування, аналогічні таким щодо ізохорного процесу (мал.7-2, б), то неважко довести, що піддотична до кривої ізобарного процесу дорівнює с_p.

Оскільки с_p > c_v, то ізобарний процес на sТ-діаграмі протікає більш полого, ніж ізохорний процес того ж газу (риc. 7-4, г).

Всі ізобари є еквідистантними кривими, що мають при одній і тій же температурі однакові кутові коефіцієнти. Горизонтальна відстань між ізобарами різних тисків визначається по рівнянню ( 6-43) при Т = const (див. мал. 7-3):

З останнього рівняння слідує, що відстань між ізобарами залежить від величини тисків і природи газу. Чим більше тиск газу, тим ізобара ближче до осі ординат.

Із зіставлення рівнянь (7-3) і (7-8) слідує, що у випадку здійснення ізохорного й ізобарного процесів в одному інтервалі температур зростання ентропії буде більше в ізобарному процесі, тому що c_р завжди більше c_v.

З мал. 7-4, б з урахуванням рівняння ( 7-7) слідує, що площа під ізобарним процесом чисельно дорівнює зміні ентальпії. Оскільки зміна ентальпії робочого тіла визначається зміною тільки його температури, то в будь-яких термодинамічних процесах, що протікають у тому самому інтервалі температур, ентальпія змінюється на те саме значення. Тому площа під ізобарним процесом на sТ-діаграмі в інтервалі температур Т₂ – T₁ дає зміну ентальпії у будь-якому іншому термодинамічному процесі, що протікає в цьому ж інтервалі температур. Отже, для визначення зміни ентальпії в довільному процесі 1-2 (рис. 7-4, в) необхідно цей процес зобразити в sТ-діаграмі, визначити T₂ і T₁, вибрати в цьому інтервалі будь-який ізобарний процес (наприклад, 1 - 3) і тоді площа під процесом 1-3, заштрихована на мал. 7-4,в, дасть зміну ентальпії у процесі 1-2.

Оскільки при ізобарному розширенні газу Т₂ > Т₁, то ∆i ₁-₂ > 0.