7 Идеальный канал без помех, канал с неопределенной фазой сигнала и аддитивным шумом, канал с межсимвольной интерференцией (мси) и аддитивным шумом

Идеальный канал без помех. Канал отображается линейной цепью с постоянной передаточной функци­ей, обычно сосредоточенной в ограниченной полосе частот Допустимы любые входные сигналы, спектр которых лежит в определенной полосе частот F_c, имеющие ограниченную среднюю мощность Р_с (либо пиковую мощность Р_пик) – ограничения характерны для всех непрерывных каналов, и в даль­нейшем о них не говорится.

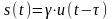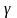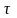В идеальном канале выходной сигнал s(t) при заданном входном u(t) де­терминирован и определяется , где – постоян­ный коэффициент передачи каната, – постоянная задержка. Эту модель ино­гда используют для описания кабельных каналов. Однако, строго говоря, она не пригодна для реальных каналов, в которых неизбежно присутствуют, хотя бы и очень слабые, аддитивные помехи.

Канал с аддитивным гауссовским шумом. Сигнал на выходе такого канала 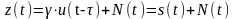, где 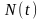– гауссовский аддитивный шум с нулевым математическим ожидани­ем и заданной корреляционной функцией Чаще всего рассматривается белый гауссовский шум (БГШ) либо квазибелый (с равномерной спектральной плот­ностью в полосе спектра сигнала s(t)). Часто при анализе можно не учиты­вать, что соответствует изменению начала отсчета времени на выходе канала, Некоторое усложнение модели получается, если коэффициенты передачи у и запаздывания т считать известными функциями времени:

.

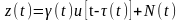Такая модель удовлетворительно описывает многие проводные каналы, ра­диоканалы при связи в пределах прямой видимости, а также радиоканалы с медленными общими замираниями, при которых можно надежно предсказать значения и .

Канал с неопределенной фазой сигнала и аддитивным шумом. Эта модель отличается от предыдущей тем, что в ней запаздывание явля­ется случайной величиной. Для узкополосных сигналов выра­жение при постоянном у и случайных т можно представить в виде

,

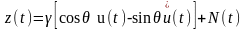где 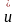- преобразование Гильберта от u(t); 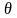= - случайная фаза. Рас­пределение вероятностей предполагается заданным, чаще всего равномерным на интервале от 0 до 2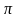 . Эта модель удовлетворительно описывает те же кана­лы, что и предыдущая, если фаза сигнала в них флуктуирует. Такая флуктуа­ция вызывается небольшими изменениями протяженности канала, свойств среды, в которой проходит сигнал, а также фазовой нестабильностью опорных генераторов.

Однолучевой гауссовский канал с общими замираниями (флуктуациями амплитуд и фаз сигнала) также описывается этой формулой, но множитель у, как и фаза , считаются случайными процессами. Иными словами, случайны­ми будут квадратурные компоненты

.

При изменении квадратурных компонент 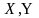во времени принимаемое ко­лебание:

.

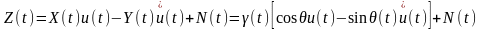Как отмечалось выше, одномерное распределение коэффициента передачи канала может быть рэлеевским или обобщенным рэлсевским. Такие каналы называют соответственно каналами с рэлеевскими или обобщенными рэлеевскими (или райсовскими) замираниями. В рамках общей гауссовской модели канала у имеет четырехпараметрическое распределение. Модель однолучевого канала с замираниями достаточно хорошо описывает многие каналы ра­диосвязи в различных диапазонах волн, а также некоторые другие каналы.

Многолучевой гауссовский канал с селективными по частоте замираниями обобщает модель:

,

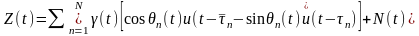где N – число лучей в канале; 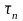– среднее время задержки для n-го луча. Многолучевая общая гауссовская модель хорошо описывает многие каналы ра­диосвязи.