
- •1 Простые типы данных языка программирования си.
- •2 Операции над данными (операция присваивания, арифметические операции, операции над битами, операции отношения, логические операции, операция условия) языка программирования си.
- •4. Операторы организации цикла
- •5.Операторы continue, break
- •15 Численные методы решение алгебраических уравнений: постановка задачи, табличный способ отделения корней.
- •16 Численные методы решение алгебраических уравнений: метод половинного деления. Метод половинного деления
- •17 Численные методы решение алгебраических уравнений: метод хорд
- •18 Численные методы решение алгебраических уравнений: метод Ньютона, модифицированный метод Ньютона. Метод Ньютона
- •19 Численные методы решение алгебраических уравнений: метод секущих. Метод секущих
- •Метод простых итераций
- •21 Численные методы решения систем линейных уравнений (слау): постановка задачи.
- •23 Численные методы решения систем линейных уравнений (слау): метод Гаусса
- •24 Численные методы решения систем линейных уравнений (слау): метод простых итераций
- •25 Численные методы решения систем линейных уравнений (слау): метод Зейделя.
- •26 Численные методы восстановления функций: постановка задачи.
- •27 Численные методы восстановления функций: интерполяция полиномом Лагранжа. Интерполяционные формулы Лагранжа и Ньютона.
- •28 Численные методы восстановления функций: погрешность интерполирования (остаточный член интерполяционной формулы и оптимальный выбор узлов).
- •2 9 Численные методы восстановления функций: интерполяция кубическим сплайном.
- •30 Численные методы восстановления функций: метод наименьших квадратов.
- •31 Методы численного интегрирования: постановка задачи, метод прямоугольников. Общие положения
- •Метод прямоугольников
- •32 Методы численного интегрирования: постановка задачи, метод трапеций. Метод трапеции
- •33 Методы численного интегрирования: постановка задачи, метод Симпсона. Метод Симпсона
- •34 Методы численного интегрирования: постановка задачи, методы Монте–Карло.
- •35 Решение математических задач в excel.
- •36 Понятие информационной системы. Виды информационных систем.
- •37 Виды и модели данных.
- •38 Понятие базы данных. Виды баз данных.
- •39 Элементы баз данных. Принципы создания базы данных. Языковые средства баз данных.
- •Работа с данными в среде FoxPro
- •Создание программных продуктов
- •Системный интерфейс FoxPro
- •Главное меню субд
- •Меню FoxPro для dos
- •Главное окно и меню FoxPro для Windows.
- •Обозначения и структура команд субд
- •Знаки операций
- •Структура команд
- •Создание файла базы данных
- •Создание структуры файла
- •Заполнение базы данных
- •Дополнение бд
- •Окно редактирования
- •Перемещения в базе данных
- •Просмотр данных
- •Удаление данных
- •Изменение данных
- •Фильтрация данных
- •Последовательный поиск
- •Продолжение поиска
- •43 Индексирование базы данных в foxpro индексирование баз данных
- •44 Работа с несколькими базами данных: связь одна запись к одной в foxpro. Работа с несколькими базами
- •Понятие о рабочих областях
- •Связь вида одна_запись_к_одной
- •Связь вида одна_запись_ко_многим
- •Команды ввода-вывода
- •Работа с переменными
- •Команды управления
- •48 Команды организации циклов в foxpro. Организация циклов Цикл с условием
- •50 Понятие компьютерной сети, назначение.
- •51Общие принципы организации и функционирования сети. Общие принципы организации и функционирования компьютерных сетей
- •52 Протоколы передачи данных в сети. Протоколы передачи данных
- •Работа протоколов
- •53 Каналы связи в сети. Типы кабелей. Беспроводная среда. Каналы связи
- •Типы кабелей
- •54 Классификация компьютерных сетей.
- •55 Локальные сети: понятие и особенности. Локальные сети
- •56 Особенности организации локальной сети: одноранговая сеть, сеть с выделенным сервером. Особенности организации локальных сетей
- •2.3.1. Одноранговая сеть
- •Сеть с выделенным сервером
- •57 Топология локальных сетей: понятие и виды. Топология локальных сетей
- •Топология "звезда"
- •58 Глобальные сети: понятие и особенности.
19 Численные методы решение алгебраических уравнений: метод секущих. Метод секущих
Далеко не всегда бывает удобно находить аналитическое выражение для производной функции, в таком случае можно использовать метод секущих.
Для начала итерационного процесса необходимо задать два начальных приближения х0 и х1.
Если
х0
и
x1
расположены достаточно близко друг к
другу, то производную
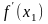 можно заменить ее приближенным значением
в виде отношения приращения функции
равного
можно заменить ее приближенным значением
в виде отношения приращения функции
равного
 к отношению приращения аргумента равного
(x1
– x0):
к отношению приращения аргумента равного
(x1
– x0):
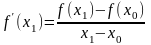 (2.4)
(2.4)
Таким образом, формула метода секущих может быть получена из формулы Ньютона (2.2) заменой производной выражением (2.4) и записана в виде:
 (2.5)
(2.5)
Однако
следует помнить, что при этом нет
необходимости, чтобы значения функции
и
 обязательно имели разный знак, как в
методе половинного деления.
обязательно имели разный знак, как в
методе половинного деления.
Процесс нахождения корня при использовании метода секущих можно считать законченным, когда выполняется следующее условие:
(2.6)
Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако не требует вычислений производной левой части уравнения.
Таким образом, для реализации метода секущих необходимо:
Задать в явном виде уравнение , корни которого необходимо определить.
Определить начальные приближения х0 и х1, обеспечивающие быструю сходимость метода.
Задать точность нахождения корня уравнения .
Реализовать в программе итерационную процедуру, реализующую формулу (2.5).
20 Численные методы простых итераций.
Метод простых итераций
Предположим, что уравнение (1) при помощи некоторых тождественных преобразований приведено к виду (2):
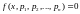 (1)
(1)
 (2)
(2)
Пусть
известно начальное приближение к корню
 ,
тогда подставим его в правую часть
уравнения (2) и получим новое приближение
(3):
,
тогда подставим его в правую часть
уравнения (2) и получим новое приближение
(3):
 (3)
(3)
Затем
аналогичным образом получим
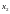 и т.д.:
и т.д.:
 (4)
(4)
З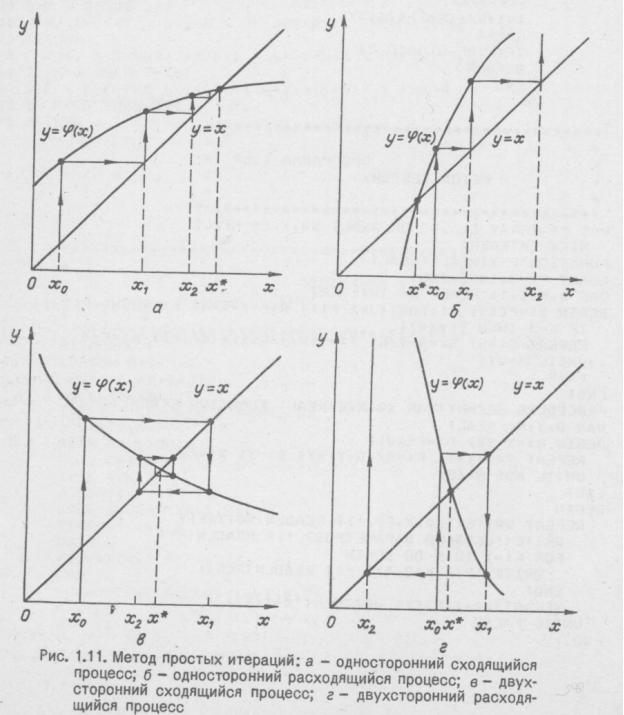 аметим:
тот факт, что
аметим:
тот факт, что
 корень уравнения
,
означает, что
есть
абсцисса точки пересечения графика
корень уравнения
,
означает, что
есть
абсцисса точки пересечения графика
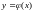 с
прямой
с
прямой
 .
.
Необходимо установить, при каких условиях итерационный процесс будет сходиться к корню уравнения .
Рассмотрим процесс графически (рисунок 1).
Рисунок 1
Из
графиков видно, что при
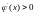 и
при
и
при
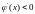 возможны
как сходящиеся, так и расходящиеся
итерационные процессы.
возможны
как сходящиеся, так и расходящиеся
итерационные процессы.
Скорость
сходимости зависит от абсолютной
величины производной функции
 .
Чем меньше
.
Чем меньше
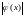 вблизи корня, тем быстрее сходится
процесс.
вблизи корня, тем быстрее сходится
процесс.
Установим теперь критерий сходимости математически.
Будем считать, что в итерационной формуле (4)
 (5)
(5)
где
 ,
,
 - отклонения k
и k+1приближения
к корню. Если процесс уточнения
осуществляется вблизи корня
,
то функцию
можно
приближенно представить двумя членами
ряда Тейлора. Тогда итерационная формула
(4) примет вид (6):
- отклонения k
и k+1приближения
к корню. Если процесс уточнения
осуществляется вблизи корня
,
то функцию
можно
приближенно представить двумя членами
ряда Тейлора. Тогда итерационная формула
(4) примет вид (6):
 (6)
(6)
но
так как
является
корнем уравнения, то
 и,
следовательно (7),
и,
следовательно (7),
 (7)
(7)
Для того чтобы итерационный процесс был сходящимся, необходимо выполнить условие (8)
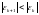 (8)
(8)
или
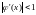
Переход
от уравнения (1) к уравнению (2) можно
осуществить разными способами в
зависимости от вида функции
 .
При таком переходе необходимо построить
функцию
так,
чтобы выполнялось условие сходимости
(8).
.
При таком переходе необходимо построить
функцию
так,
чтобы выполнялось условие сходимости
(8).
Рассмотрим один из общих алгоритмов перехода от уравнения (1) к уравнению (2).
Умножим
левую и правую части уравнения (1) на
произвольную константу
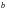 и
добавим к обеим частям неизвестное
и
добавим к обеим частям неизвестное
 .
При этом корни исходного уравнения не
изменятся (9):
.
При этом корни исходного уравнения не
изменятся (9):
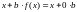 (9)
(9)
Введем обозначение (10)
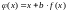 (10)
(10)
и перейдем от соотношения (9) к уравнению (2).
Произвольный
выбор константы
позволит
обеспечить выполнение условия сходимости
(8). Желательно выбрать величину
такой,
чтобы
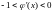 ,
тогда сходимость итерационного процесса
будет двухсторонней. В этом случае в
наиболее простом виде можно представить
критерий окончания итерационного
процесса (11)
,
тогда сходимость итерационного процесса
будет двухсторонней. В этом случае в
наиболее простом виде можно представить
критерий окончания итерационного
процесса (11)
 (11)
(11)
где
 -
заданная абсолютная погрешность
вычисления корня.
-
заданная абсолютная погрешность
вычисления корня.
Если функция выбрана в виде (1.33), то производная по от этой функции будет (12)
 (12)
(12)
Наибольшую
скорость сходимости получим при
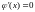 ,
тогда
,
тогда

и итерационная формула (4) переходит в формулу Ньютона (13)

