
- •1 Простые типы данных языка программирования си.
- •2 Операции над данными (операция присваивания, арифметические операции, операции над битами, операции отношения, логические операции, операция условия) языка программирования си.
- •4. Операторы организации цикла
- •5.Операторы continue, break
- •15 Численные методы решение алгебраических уравнений: постановка задачи, табличный способ отделения корней.
- •16 Численные методы решение алгебраических уравнений: метод половинного деления. Метод половинного деления
- •17 Численные методы решение алгебраических уравнений: метод хорд
- •18 Численные методы решение алгебраических уравнений: метод Ньютона, модифицированный метод Ньютона. Метод Ньютона
- •19 Численные методы решение алгебраических уравнений: метод секущих. Метод секущих
- •Метод простых итераций
- •21 Численные методы решения систем линейных уравнений (слау): постановка задачи.
- •23 Численные методы решения систем линейных уравнений (слау): метод Гаусса
- •24 Численные методы решения систем линейных уравнений (слау): метод простых итераций
- •25 Численные методы решения систем линейных уравнений (слау): метод Зейделя.
- •26 Численные методы восстановления функций: постановка задачи.
- •27 Численные методы восстановления функций: интерполяция полиномом Лагранжа. Интерполяционные формулы Лагранжа и Ньютона.
- •28 Численные методы восстановления функций: погрешность интерполирования (остаточный член интерполяционной формулы и оптимальный выбор узлов).
- •2 9 Численные методы восстановления функций: интерполяция кубическим сплайном.
- •30 Численные методы восстановления функций: метод наименьших квадратов.
- •31 Методы численного интегрирования: постановка задачи, метод прямоугольников. Общие положения
- •Метод прямоугольников
- •32 Методы численного интегрирования: постановка задачи, метод трапеций. Метод трапеции
- •33 Методы численного интегрирования: постановка задачи, метод Симпсона. Метод Симпсона
- •34 Методы численного интегрирования: постановка задачи, методы Монте–Карло.
- •35 Решение математических задач в excel.
- •36 Понятие информационной системы. Виды информационных систем.
- •37 Виды и модели данных.
- •38 Понятие базы данных. Виды баз данных.
- •39 Элементы баз данных. Принципы создания базы данных. Языковые средства баз данных.
- •Работа с данными в среде FoxPro
- •Создание программных продуктов
- •Системный интерфейс FoxPro
- •Главное меню субд
- •Меню FoxPro для dos
- •Главное окно и меню FoxPro для Windows.
- •Обозначения и структура команд субд
- •Знаки операций
- •Структура команд
- •Создание файла базы данных
- •Создание структуры файла
- •Заполнение базы данных
- •Дополнение бд
- •Окно редактирования
- •Перемещения в базе данных
- •Просмотр данных
- •Удаление данных
- •Изменение данных
- •Фильтрация данных
- •Последовательный поиск
- •Продолжение поиска
- •43 Индексирование базы данных в foxpro индексирование баз данных
- •44 Работа с несколькими базами данных: связь одна запись к одной в foxpro. Работа с несколькими базами
- •Понятие о рабочих областях
- •Связь вида одна_запись_к_одной
- •Связь вида одна_запись_ко_многим
- •Команды ввода-вывода
- •Работа с переменными
- •Команды управления
- •48 Команды организации циклов в foxpro. Организация циклов Цикл с условием
- •50 Понятие компьютерной сети, назначение.
- •51Общие принципы организации и функционирования сети. Общие принципы организации и функционирования компьютерных сетей
- •52 Протоколы передачи данных в сети. Протоколы передачи данных
- •Работа протоколов
- •53 Каналы связи в сети. Типы кабелей. Беспроводная среда. Каналы связи
- •Типы кабелей
- •54 Классификация компьютерных сетей.
- •55 Локальные сети: понятие и особенности. Локальные сети
- •56 Особенности организации локальной сети: одноранговая сеть, сеть с выделенным сервером. Особенности организации локальных сетей
- •2.3.1. Одноранговая сеть
- •Сеть с выделенным сервером
- •57 Топология локальных сетей: понятие и виды. Топология локальных сетей
- •Топология "звезда"
- •58 Глобальные сети: понятие и особенности.
16 Численные методы решение алгебраических уравнений: метод половинного деления. Метод половинного деления
Для
применения метода половинного деления
необходимо установить окрестность или
отрезок [a,
b], на котором
расположен один из корней уравнения,
который необходимо уточнить с погрешностью
Е
(рис.2.1).
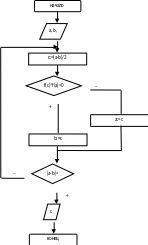

Рис. 2.1. Метод половинного деления.
Пусть
дано уравнение
 ,
где
,
где
 непрерывна на отрезке [a,
b] и
непрерывна на отрезке [a,
b] и
 .
.
Метод половинного деления, или дихотомии, заключается в следующем. Для нахождения корня уравнения, принадлежащего отрезку [a, b], делим отрезок пополам, т.е. выбираем начальное приближение, равное:

и
вычисляем значение функции
 .
Если
.
Если
 ,
то
,
то
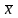 является корнем уравнения. Если
является корнем уравнения. Если
 ,
то выбираем, одну из двух частей отрезка
,
то выбираем, одну из двух частей отрезка
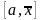 или
или
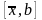 для дальнейшего уточнения корня.
Естественно, что корень будет находиться
в той половине отрезка, на концах которого
функция
имеет разные знаки, а именно проверяем
условие:
для дальнейшего уточнения корня.
Естественно, что корень будет находиться
в той половине отрезка, на концах которого
функция
имеет разные знаки, а именно проверяем
условие:
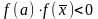 .
На рис.2.1 это будет отрезок
,
т. е. для очередного шага уточнения точку
b
перемещаем в середину отрезка
.
На рис.2.1 это будет отрезок
,
т. е. для очередного шага уточнения точку
b
перемещаем в середину отрезка
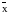 (b=
)
и продолжаем процесс деления как с
первоначальным отрезком [a,
b].
(b=
)
и продолжаем процесс деления как с
первоначальным отрезком [a,
b].
Итерационный (повторяющийся) процесс деления будет продолжаться до тех пор, пока не будет выполнено условие:
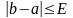 .
.
За приближенное решение принимается средняя точка последнего промежутка.
Таким образом, для реализации метода дихотомии необходимо:
Задать в явном виде уравнение , корни которого необходимо определить.
Определить начальный интервал [a, b], внутри которого лежит корень.
Задать точность нахождения корня уравнения .
Реализовать в программе итерационную процедуру, описанную выше.
17 Численные методы решение алгебраических уравнений: метод хорд



18 Численные методы решение алгебраических уравнений: метод Ньютона, модифицированный метод Ньютона. Метод Ньютона
П редположим,
что у нас определено начальное приближение
х0
к одному из корней уравнения (2.1). Тогда
в точке х0
можно вычислить левую часть решаемого
уравнения
редположим,
что у нас определено начальное приближение
х0
к одному из корней уравнения (2.1). Тогда
в точке х0
можно вычислить левую часть решаемого
уравнения
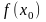 .
.
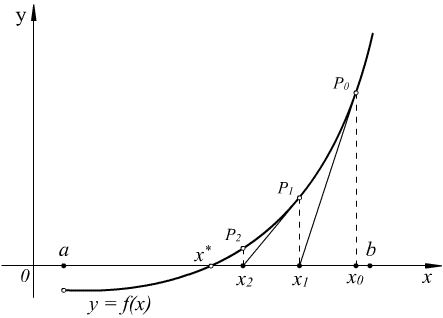
Рис.2.2. Метод Ньютона
Рассмотрение
метода Ньютона начнем с его геометрического
представления (рис. 2.2). Возьмем точку
х0
отрезка [a,
b]
и проведем
в точке P0
с координатами
 касательную к кривой y=
до пересечения с осью 0х.
Получим значение х1,
в котором касательная пересекает ось
0x.
Угловой коэффициент касательной равен
значению производной от функции
в точке
касания. Следовательно, уравнение
касательной, проходящей через точку с
координатами
имеет вид :
касательную к кривой y=
до пересечения с осью 0х.
Получим значение х1,
в котором касательная пересекает ось
0x.
Угловой коэффициент касательной равен
значению производной от функции
в точке
касания. Следовательно, уравнение
касательной, проходящей через точку с
координатами
имеет вид :
 .
.
Полагая y=0, находим точку пересечения касательной с осью 0х, которую обозначим через х1:
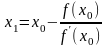
Абсциссу
х1
точки пересечения можно взять в качестве
приближенного значения корня. Проведя
касательную через новую точку с
координатами
 и находя
точку ее пересечения с осью 0х,
получим второе приближения корня х2
. Аналогично определяются последующие
приближения.
и находя
точку ее пересечения с осью 0х,
получим второе приближения корня х2
. Аналогично определяются последующие
приближения.
Следующие приближения находим соответственно по формулам:

……………………

В общем случае для k-го шага итерационного процесса последнее соотношение принимает вид:
 (2.2)
(2.2)
Из
формулы (2.2) вытекает необходимость
вычисления значения производной функции
в каждой точке. Процесс нахождения корня
может считаться законченным, когда
модуль отношения значения функции в
точке xk
к ее производной меньше заданной величины
погрешности
 ,
т.е. когда выполняется следующее условие:
,
т.е. когда выполняется следующее условие:
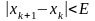 (2.3)
(2.3)
Таким образом, для реализации метода Ньютона необходимо:
Задать в явном виде уравнение , корни которого необходимо определить.
Определить первую производную функции в аналитическом виде.
Определить начальное приближение х0, обеспечивающее быструю сходимость метода.
Задать точность нахождения корня уравнения .
Реализовать в программе итерационную процедуру, реализующую формулу (2.2).
