
- •12. Теорема – необходимое условие линейной независимости решений линейного однородного дифференциального уравнения.
- •13.Теорема о структуре общего решения линейного однородного дифференциального уравнения.
- •14.Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.
- •15. Метод вариации произвольных постоянных.
- •16.Линейные однородные дифференциальные уравнения с постоянными коэффициентами (для 2-го порядка).
- •Уравнение второго порядка
- •17.Линейные однородные дифференциальные уравнения с постоянными коэффициентами (для n-го порядка).
- •Уравнение порядка n
- •18.Неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида.
- •19.Системы дифференциальных уравнений. Нормальная система дифференциальных уравнений. Задача Коши. Решение системы дифференциальных уравнений методом исключения. Пример.
- •Примеры нормальных форм
- •Различные постановки задачи Коши
- •Теоремы о разрешимости задачи Коши для оду
- •Метод исключения — сведение системы ду к одному уравнению
- •20.Комплексные числа. Алгебраическая, тригонометрическая и показательная формы.
- •Определения
- •Стандартная модель
- •Связанные определения
- •Модуль и аргумент
- •Сопряжённые числа
- •Представление комплексных чисел Алгебраическая форма
- •Тригонометрическая и показательная формы
Модуль и аргумент
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль
комплексного числа z обозначается | z | и
определяется выражением ![]() .
Часто обозначается буквами
.
Часто обозначается буквами ![]() или
или ![]() .
Если z является вещественным
числом,
то | z | совпадает
с абсолютной
величиной этого
вещественного числа.
.
Если z является вещественным
числом,
то | z | совпадает
с абсолютной
величиной этого
вещественного числа.
Для
любых ![]() имеют
место следующие свойства модуля. :
имеют
место следующие свойства модуля. :
1) ![]() ,
причём
,
причём ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() ;;
;;
2) ![]() (неравенство
треугольника);
(неравенство
треугольника);
3) ![]() ;
;
4) ![]() .
.
Из
третьего свойства следует ![]() ,
где
,
где ![]() .
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру
двумерного нормированного
пространства над
полем
.
.
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру
двумерного нормированного
пространства над
полем
.
5) Для пары комплексных чисел z1 и z2 модуль их разности | z1 − z2 | равен расстоянию между соответствующими точками комплексной плоскости.
Угол ![]() (в
радианах) радиус-вектора точки,
соответствующей числу z,
называется аргументом числа z и
обозначается
(в
радианах) радиус-вектора точки,
соответствующей числу z,
называется аргументом числа z и
обозначается ![]() .
.
Из этого определения следует, что
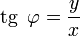 ;
; 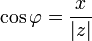 ;
; 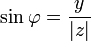 .
.Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2kπ, где k — любое целое число.
Главным значением аргумента называется такое значение , что
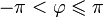 .
Часто главное значение обозначается
.
Часто главное значение обозначается 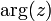 [4].
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного:
[4].
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного:
![]() .
.
Сопряжённые числа
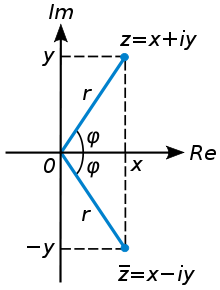
Геометрическое представление сопряжённых чисел
Если
комплексное число z = x + iy,
то число ![]() называется сопряжённым (или
комплексно сопряжённым) к z(обозначается
также z * ).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
называется сопряжённым (или
комплексно сопряжённым) к z(обозначается
также z * ).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
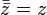 (сопряжённое
к сопряжённому есть исходное).
(сопряжённое
к сопряжённому есть исходное).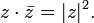
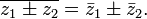
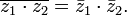
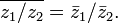
Обобщение: ![]() ,
где p(z) —
произвольный многочлен с вещественными
коэффициентами.
,
где p(z) —
произвольный многочлен с вещественными
коэффициентами.
Значимость
сопряжения объясняется тем, что оно
является образующей группы
Галуа ![]() .
.
Представление комплексных чисел Алгебраическая форма
Запись
комплексного числа z в
виде x + iy, ![]() ,
называется алгебраической
формой комплексного
числа.
,
называется алгебраической
формой комплексного
числа.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2 = − 1):
(a + ib) + (c + id) = (a + c) + i(b + d);
![]()
Тригонометрическая и показательная формы
Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме
z = r(cos φ + isin φ).
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
z = reiφ,
где eiφ — расширение экспоненты для случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
![]()
