
- •9 Понятие деления. Структура деления. Виды деления. Правила деления и возможные ошибки.
- •Суждение
- •[Править]По отношению между подлежащим и сказуемым
- •]Другие
- •22. Законы логики
- •31. Фигуры простого категорического силлогизма, их правила и значения.
- •33. Умозаключения изложенных суждений. Их виды.
- •§ 2. Виды аналогии
- •§ 2. Состав аргументации: субъекты, структура Субъекты аргументации
- •1. Правила и условия, относящиеся к тезису.
- •2. Правила и условия, относящиеся к аргументам.
- •3. Правила и условия, относящиеся к демонстрации.
- •Уловка в доказательстве
- •Виды спора
- •1. Правила и условия, относящиеся к тезису.
- •2. Правила и условия, относящиеся к аргументам.
- •3. Правила и условия, относящиеся к демонстрации.
- •Уловка в доказательстве
- •Виды спора
31. Фигуры простого категорического силлогизма, их правила и значения.
Первая
фигура силлогизма- это такое расположение
его терминов, при котором первая посылка
начинается со среднего термина, а вторая
заканчивается средним термином. Пример:

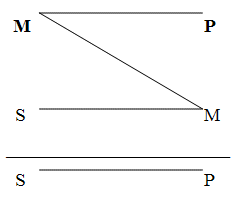
Вторая фигура силлогизма- это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Пример:

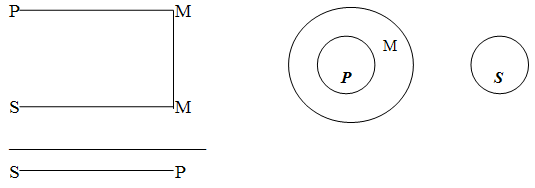
Третья фигура силлогизма- это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Пример:

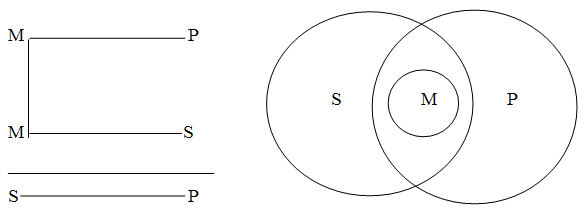
Четвертая фигура силлогизма- это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Пример:
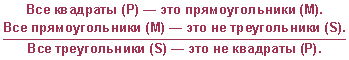
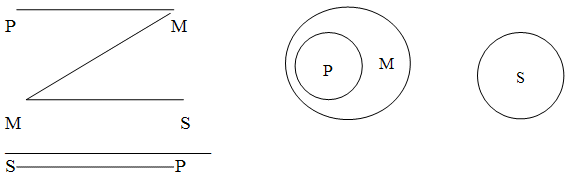
Правила категорического силлогизма:
Правила терминов. 1. В каждом силлогизме должно быть только три термина (S, P, M). 2. Средний термин должен быть распределен по крайней мере в одной из посылок. 3. Термин распределен в заключении, если и только если он распределен в посылках, поэтому заключение ложное.
Правило посылок. 1. Из двух отрицательных посылок нельзя сделать никакого заключения. 2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным. Если одна из посылок частная, то и заключение должно быть частным.
32. Модусы силлогизма. Правила выводов модуса. Модусами категорического силлогизма называются разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключения. Модус простого силлогизма составляет три суждения. Например, в силлогизме:
Все небесные тела движутся.
Все планеты — это небесные тела.
------------
Все планеты движутся.
Первая посылка является простым суждением вида А (общеутвердительным), вторая посылка — это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус ААА. Силлогизм:
Все журналы периодические издания.
Все книги не являются периодическими изданиями.
------------
Все книги не являются журналами.
имеет модус АЕЕ. Силлогизм:
Все углероды простые тела.
Все углероды электропроводны.
------------
Некоторые электропроводники — простые тела.
имеет модус ААI. Всего модусов во всех четырех фигурах, то есть возможных комбинаций простых суждений в силлогизме, — 256. В каждой фигуре 64 модуса. Однако из всех этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность ее выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные — неправильными.
Правила вывода модуса. Modus ponens (правило заключения): если A и A→B — выводимые формулы, то B также выводима.
Форма записи: ![]() ,
где A, B —
любые формулы.
,
где A, B —
любые формулы.
Modus ponens — правило вывода в исчислении высказываний. Является частным случаем правила резолюций.
33. Умозаключения изложенных суждений. Их виды.
34.Силлогизм – это такое умозаключение, в котором из двух суждений получается третье суждение, называемое выводом.
В медицине чаще всего пользуются следующими силлогизмами:
- категорическим силлогизмом первой фигуры;
- категорическим силлогизмом второй фигуры;
- условно-категорическим силлогизмом;
- разделительным силлогизмом.
Для того чтобы создать силлогизм, требуется сопоставить два суждения (посылки). Первое суждение называется большим, второе – меньшим. Помимо субъекта и предиката, которые в силлогизме используются как посылки, в суждениях обязательно наличествует так называемый средний термин. Указанный средний термин играет особую связующую роль, но отсутствует в выводе.
Категорический силлогизм первой фигуры
Это умозаключение имеет следующую структуру.
М-Р.
S-M.
Следовательно, S есть Р.
S и Р являются субъектом и предикатом (подлежащим и сказуемым) суждений, а М (medius) представлен средним термином. Мы сопоставили субъект и предикат с грамматическим сказуемым и подлежащим. Это следует рассматривать лишь как сравнение, ибо субъектом в суждении может выступать сразу несколько слов. То же самое относится к предикату.
Категорический силлогизм первой фигуры в логике уже более 2 тысяч лет относится к самым достоверным и убедительным умозаключениям. В медицине данный силлогизм очень часто применяется для доказательства или отрицания самых разных положений.
Для правильного построения первой фигуры категорического силлогизма необходимо соблюсти два правила:
1. Большая посылка всегда носит общий характер, но может быть утвердительной или отрицательной. Другими словами, большая посылка заключает в себе общее и достоверное знание утверждающего или отрицающего характера.
2. Меньшая посылка всегда утвердительная.
В зависимости от содержания (утвердительного или отрицательного) большей посылки умозаключение по первой фигуре носит вид подтверждающего или отрицающего суждения.
Категорический силлогизм второй фигуры
Этот силлогизм предназначен только для достоверного отрицания, для доказательства отсутствия сходства между понятиями или признаками. Структура его такова:
Р-М.
S-M.
Cледовательно, S не есть Р.
В практической жизни данный вид силлогизма настолько привычен в мышлении, что им пользуются в сокращенном виде, мысленно убирая большую посылку, вернее, подразумевая ее.
Условно-категорический силлогизм
Условно-категорическим силлогизмом называется такой вид умозаключения, в котором большая посылка представлена условным суждением, а меньшая посылка представляет собой категорическое суждение. В результате вывод (умозаключение) носит также категорический характер.
Вследствие комбинаций утвердительных и отрицательных форм составных частей суждения, условно-категорические силлогизмы делятся на 4 модуса (разновидности).
Разберем вначале первый модус, который называется утверждающим (modus ponens) и в сокращенной форме имеет следующий вид:
Если Б-Р, toS1-P1.
S есть Р.
Следовательно, S1 есть Р1
Первая посылка в данном типе силлогизма всегда представлена условным суждением типа «если…, то…». Условие, выраженное в суждении «если S – Р», называется основанием, а вторая часть первой посылки в виде суждения S, – Р| именуется следствием. Когда в меньшей посылке (доктор А. является хорошим диагностом) нечто подтверждает условие, то вывод, т.е. следствие, считается доказанным. Другими словами, в утверждающем модусе из истинности основания вытекает правильность следствия.
Второй логически правильный модус условно-категорического силлогизма именуется отрицающим (modus tollens) и имеет следующий вид:
Если S – Р, то S, – Р,
Si не есть Р,
Следовательно, S не есть Р.
Этот модус основан на логическом правиле, что из ложности следствия вытекает неистинность основания.
Повторяем два главных правила условно-категорических силлогизмов, соблюдение которых оформляет наше знание логически безупречным образом:
1) из истинности основания следует истинность следствия;
2) из ложности следствия вытекает ошибочность основания.
Только два указанных модуса дают верное знание с точки зрения логики: подтверждающий и отрицающий.
Условно-категорический силлогизм, как и другие виды дедуктивных умозаключений, нужен для вывода частного знания из общего закона. Этот тип силлогизма предназначен для выяснения истинности логической связи между двумя явлениями, между причиной и следствием. Условно-категорический силлогизм в выводе позволяет получать высокодостоверное знание. Это подтверждается той легкостью, с которой условно-категорический силлогизм превращается в категорический и обратно. Для этой операции лишь меняется грамматическая структура первой (большей) посылки.
Два оставшихся модуса условно-категорического силлогизма дают неопределенное или неправильное знание. Для того чтобы предостеречь вас от использования этих неправильных модусов, приведем их формулы и дадим примеры:
Если S – Р, то S1 – P1
S не есть Р.
Следовательно, S1 не есть Р1.
Это неправильный отрицающий модус, где из ложности основания не может быть выведена ложность следствия. Другими словами, если мы связываем два суждения причинной связью, но при этом отрицаем (считаем ложным) основание (S не есть Р), то следствие, или вывод, становится неопределенным..
Также неверным предстает модус условно-категорического силлогизма следующей формулы:
Ecjih S-P, то S1-Р1.
S1 есть Р1.
Следовательно, S есть Р.
Этот модус якобы выводит истинность основания из истинности следствия. Данный вид ошибки в логике именуется «после того, значит вследствие того» (post hoc ergo propter hoc).
Человеческое мышление склонно связывать причинно-следственными отношениями события, которые следуют одно за другим. В части случаев это оказывается правильным, но в целом нельзя увязывать два факта только по той причине, что один следовал за другим.
Разделительный силлогизм
Это такой силлогизм, в котором по крайней мере большая посылка является разделительным суждением.
Мы уже напоминали о чрезвычайной важности разделительных суждений для дифференциального диагноза. По сути вся дифференциальная диагностика строится по схеме утвердительного (чаще) или отрицательного разделительного умозаключения.
Схема утвердительного разделительного силлогизма:
S есть или Р1 или Р2, или Р3.
S не оказался ни Р1 ни Р2.
Следовательно, S есть Р3.
Схема отрицательного разделительного силлогизма:
S есть или Р1 или Р2, или Р3.
S есть Р|.
Следовательно, S не является ни Р2, ни Р3
Существуют два правила построения разделительных силлогизмов:
1. В большей посылке должны быть перечислены все члены дизъюнкции. Другими словами, объем предикатов должен равняться объему субъекта, иначе вывод не будет доказательным.
2. Предикаты должны исключать друг друга и не перекрещиваться. Нарушение данного правила ведет к тому, что суждение в малой посылке «S есть Pi» не вполне точно отражает действительность, и это неизбежно повлияет на достоверность вывода.
35.
Разделительно-категорический и чисто разделительный силлогизмы
Умозаключения, которые содержат в себе разделительные, (дизъюнктивные) суждения называются разделительными. В мышлении и речи часто используется разделительно-категорический силлогизм, в котором, как явствует из названия, первая посылка представляет собой разделительное (дизъюнктивное) суждение, а вторая посылка – простое (категорическое). Например:
Учебное заведение может быть начальным, или средним, или высшим. МГУ является высшим учебным заведением. МГУ – это не начальное и не среднее учебное заведение.
Разделительно-категорический силлогизм имеет два модуса:
1. Утверждающе-отрицающий модус, у которого первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, вторая утверждает один из них, а вывод отрицает все остальные (таким образом, рассуждение движется от утверждения к отрицанию). Например:
Леса бывают хвойными, или лиственными, или смешанными. Этот лес хвойный. Этот лес не лиственный и не смешанный.
С помощью условных обозначений логических союзов можно представить форму данного силлогизма в виде следующей записи:
(( a b c) ? a)?(¬ b? ¬ c), где ( a b c) – это первая посылка в виде строгой дизъюнкции трёх простых суждений; a– это вторая посылка в виде утверждения одного из них; (( a b c) ? a) – это две посылки силлогизма, соединённые знаком конъюнкции; (¬ b? ¬ c) – это вывод силлогизма в виде конъюнкции отрицаний двух оставшихся простых суждений, входивших в первую посылку; знак импликации «?» показывает, что из посылок следует вывод.
2. Отрицающе-утверждающий модус, у которого первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, вторая отрицает все данные варианты, кроме одного, а вывод утверждает один оставшийся вариант (таким образом, рассуждение движется от отрицания к утверждению).
Например:
Люди бывают европеоидами, или монголоидами, или негроидами. Этот человек не монголоид и не негроид. Этот человек является европеоидом.
С помощью условных обозначений логических союзов можно представить форму данного силлогизма в виде следующей записи:
(( a b c) ? (¬ b? ¬ c)) ? a, где ( a b c) – это первая посылка в виде строгой дизъюнкции трёх простых суждений; (¬ b?¬ c) – это вторая посылка в виде конъюнкции отрицаний двух из них;
( a b c) ? (¬ b?¬ c) – это две посылки силлогизма, соединённые знаком конъюнкции; a– это вывод силлогизма в виде утверждения третьего простого суждения, входившего в первую посылку; и наконец, импликацией объединяются посылки и вывод силлогизма.
Первая посылка разделительно-категорического силлогизма является строгой дизъюнкцией, т. е. представляет собой уже знакомую нам логическую операцию деления понятия. Поэтому неудивительно, что правила этого силлогизма повторяют известные нам правила деления понятия:
1. Деление в первой посылке должно проводиться по одному основанию. Например:
Транспорт бывает наземным, или подземным, или водным, или воздушным, или общественным. Пригородные электропоезда – это общественный транспорт. Пригородные электропоезда – это не наземный, не подземный, не водный и не воздушный транспорт.
Силлогизм построен по утверждающе-отрицающему модусу: в первой посылке представлено несколько вариантов, во второй посылке один из них утверждается, в силу чего в выводе отрицаются все остальные. Однако из двух истинных посылок вытекает ложный вывод. Почему так получается? Потому что в первой посылке деление проводилось по двум разным основаниям: в какой природной среде передвигается транспорт и кому он принадлежит. Подмена основания деления в первой посылке разделительно-категорического силлогизма приводит к ложному выводу.
2. Деление в первой посылке должно быть полным. Например:
Математические действия бывают сложением, или вычитанием, или умножением, или делением. Логарифмирование – это не сложение, не вычитание, не умножение и не деление. Логарифмирование – это не математическое действие.
В силлогизме неполное деление в первой посылке обусловливает ложный вывод, вытекающий из истинных посылок.
3. Результаты деления в первой посылке не должны пересекаться, или дизъюнкция должна быть строгой. Например:
Страны мира бывают северными, или южными, или западными, или восточными. Канада – это северная страна. Канада – это не южная, не западная и не восточная страна.
В силлогизме вывод является ложным, т. к. Канада в такой же степени северная страна, в какой и западная. Ложный вывод при истинных посылках объясняется в данном случае пересечением результатов деления в первой посылке, или, что одно и то же, – нестрогой дизъюнкцией .Следует отметить, что нестрогая дизъюнкция в разделительно-категорическом силлогизме допустима в том случае, когда он построен по отрицающе-утверждающему модусу. Например:
Он силён от природы или же постоянно занимается спортом. Он не является сильным от природы. Он постоянно занимается спортом.
В силлогизме нет ошибки, несмотря на то, что дизъюнкция в первой посылке была нестрогой. Таким образом, рассматриваемое правило безоговорочно действует только для утверждающе-отрицающего модуса разделительно-категорического силлогизма.
4. Деление в первой посылке должно быть последовательным. Например:
Предложения бывают простыми, или сложными, или сложносочинёнными.
Это предложение сложносочинённое. Это предложение не простое и не сложное.
В силлогизме ложный вывод следует из истинных посылок по той причине, что в первой посылке был допущен скачок в делении.
Разделительно-категорический силлогизм в логике часто называют просто разделительно-категорическим умозаключением. Помимо него существует также чисто разделительный силлогизм( чисто разделительное умозаключение), обе посылки и вывод которого являются разделительными (дизъюнктивными) суждениями.
Например:
Зеркала бывают плоскими или сферическими. Сферические зеркала бывают вогнутыми или выпуклыми. Зеркала бывают плоскими, или вогнутыми, или выпуклыми.
Форму приведённого чисто разделительного силлогизма можно представить следующим образом: (( a b) ? ( b 1 b 2)) ? ( a b 1 b 2), где ( a b) – первая посылка; ( b 1 b 2) – вторая посылка; ( a b 1 b 2) – вывод.
36.
Условно-категорический, эквивалентно-категорический и чисто условный силлогизмы
Умозаключения, которые содержат в себе условные (импликативные) суждения называются условными. В мышлении и речи часто используется условно-категорический силлогизм, название которого свидетельствует о том, что в нём первая посылка является условным (импликативным) суждением, а вторая посылка – простым (категорическим). Например:
Если взлётная полоса покрыта льдом, то самолёты не могут взлетать.
Сегодня взлётная полоса покрыта льдом.
Сегодня самолёты не могут взлетать.
Условно-категорический силлогизм имеет два модуса:
1. Утверждающий модус, у которого первая посылка представляет собой импликацию, состоящую, как мы уже знаем, из двух частей – основания и следствия, вторая посылка является утверждением основания, а в выводе утверждается следствие. Например:
Если вещество – металл, то оно электропроводно.
Данное вещество – это металл.
Данное вещество электропроводно.
Форма утверждающего модуса условно-категорического силлогизма: (( a? b) ? a) ? b, где ( a? b) – это первая посылка в виде импликации основания и следствия; (( a? b) ? a) – это две посылки силлогизма в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и утверждения основания; b– это вытекающий из посылок вывод силлогизма в виде утверждения следствия.
2. Отрицающий модус, у которого первая посылка представляет собой импликацию основания и следствия, вторая посылка является отрицанием следствия, а в выводе отрицается основание.
Например:
Если вещество – металл, то оно электропроводно.
Данное вещество неэлектропроводно.
Данное вещество – не металл.
Форма отрицающего модуса условно-категорического силлогизма: (( a? b) ?¬ b) ? ¬ a, где ( a? b) – это первая посылка в виде импликации основания и следствия; (( a? b) ? ¬ b) – это две посылки силлогизма в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и отрицания следствия; ¬ a– это вытекающий из посылок вывод силлогизма в виде отрицания основания.
Необходимо обратить внимание на уже известную нам особенность импликативного суждения, которая состоит в том, что основание и следствие нельзя поменять местами. Например, высказывание: « Если вещество – металл, то оно электропроводно», – является верным, т. к. все металлы – это электропроводники (из того, что вещество – металл, с необходимостью вытекает его электропроводность). Однако высказывание: « Если вещество электропроводно, то оно – металл», – неверно, т. к. не все электропроводники являются металлами (из того, что вещество электропроводно, не вытекает то, что оно – металл). Эта особенность импликации обусловливает два правила условно-категорического силлогизма:
1. Утверждать можно только от основания к следствию, т. е. во второй посылке утверждающего модуса должно утверждаться основание импликации (первой посылки), а в выводе – её следствие.
В противном случае из двух истинных посылок может вытекать ложный вывод. Например:
Если слово стоит в начале предложения, то его надо писать с большой буквы.
Слово «Москва» надо писать с большой буквы.
Слово «Москва» всегда стоит в начале предложения.
В силлогизме во второй посылке утверждалось следствие, а в выводе – основание: (( a? b) ? b) ? a. Это утверждение от следствия к основанию и является причиной ложного вывода при истинных посылках.
2. Отрицать можно только от следствия к основанию, т. е. во второй посылке отрицающего модуса должно отрицаться следствие импликации (первой посылки), а в выводе – её основание. В противном случае из двух истинных посылок может вытекать ложный вывод. Например:
Если слово стоит в начале предложения, то его надо писать с большой буквы.
В данном предложении слово «Москва» не стоит в начале.
В данном предложении слово «Москва» не надо писать с большой буквы.
В силлогизме во второй посылке отрицается основание, а в выводе – следствие: (( a? b) ? ¬ a) ? ¬ b. Это отрицание от основания к следствию и является причиной ложного вывода при истинных посылках.
Вспомним, что среди сложных суждений помимо импликации: a? b, есть также эквиваленция: a b. Если в импликации всегда выделяется основание и следствие, то в эквиваленции нет ни того, ни другого, т. к. она представляет собой сложное суждение, обе части которого тождественны (эквивалентны) друг другу. Если первой посылкой силлогизма является не импликация, а эквиваленция, то такой силлогизм называется эквивалентно-категорическим. Например:
Если число чётное, то оно делится без остатка на 2.
Число 16 – чётное.
Число 16 делится без остатка на 2.
Форма модуса данного силлогизма: ( a b) ? a) ? b.
Поскольку в первой посылке эквивалентно-категорического силлогизма нельзя выделить ни основания, ни следствия, то рассмотренные выше правила условно-категорического силлогизма к нему неприменимы (в эквивалентно-категорическом силлогизме и утверждать, и отрицать можно как угодно). Если в условно-категорическом силлогизме два модуса правильных и два неправильных (см. выше), то в эквивалентно-категорическом силлогизме все четыре модуса являются правильными:
(( a b) ? a) ? b;
(( a b) ? b) ? a;
(( a b) ? ¬ a) ? ¬ b;
(( a b) ? ¬ b) ? ¬ a.
Читатель без труда сможет подобрать примеры для каждого из четырёх модусов эквивалентно-категорического силлогизма.
Если же обе посылки и вывод представляют собой условные суждения, то это чисто условный силлогизм (чисто условное умозаключение). Например:
Если вещество является металлом, то оно электропроводно.
Если вещество электропроводно, то его невозможно использовать в качестве изолятора.
Если вещество является металлом, то его невозможно использовать в качестве изолятора.
Форма модуса данного силлогизма: (( a? b) ? ( b? c)) ? ( a? c).
37.
Энтимéма (др.-греч. ἐνθύμημα) — сокращённый силлогизм, в котором в явной форме не выражена посылка или заключение, однако пропущенный элемент подразумевается.
Иногда к энтимеме прибегают нарочно, желая получить неожиданное заключение. Эффект остроумия в значительной степени зависит от энтимемы.
Согласно Аристотелю («Риторика»), энтимема представляет собой «риторический силлогизм»: его цель — убеждение, в отличие от полного «научного» силлогизма, используемого для доказательства.
В теории аргументации энтимема — неполно приведённый аргумент, недостающие части которого подразумеваются очевидными.[1]
Виды энтимем:
С пропущенной большей посылкой
С пропущенной меньшей посылкой
С пропущенным заключением
38. Как же восстанавливать энтимену в полный силлогизм?
Здесь могут встретиться некоторые трудности.
Давайте возьмем пример попроще:
«Земля планета, потому что она вращается вокруг солнца».
Это энтимема. Верна ли она?
Сначала нужно понять: что нам дано в энтимене – две посылки или одна посылка и вывод? Слова «потому что» намекают на то, что первое предложение нашей энтимены является выводом, а второе – посылкой, из которой он следует.
Запишем их как посылку и вывод силлогизма.
Земля вращается вокруг солнца.
Земля планета!
Вывод у нас есть. По выводу мы определяем, что меньшим термином силлогизма является понятие «Земля», а большим – понятие «планета».
Мы видим далее, что в нашу посылку входит меньший термин «Земля», следовательно, нам дана меньшая посылка.
Опущена и подразумевается большая посылка. Ещё одно понятие, входящие в нашу посылку, - «вращается вокруг Солнца» - должно быть средним термином силлогизма. Таким образом , у нас имеется средний термин и большой термин – всё, что требуется для восстановления опущенной большой посылки.
Однако её можно сформулировать двояким образом
«М – Р» или «Р – М».
Ну что же, сформулируем два силлогизма:
Все планеты вращаются вокруг Солнца.
Земля вращается вокруг Солнца.
Земля - планета.
Некоторые тела, вращающиеся вокруг солнца, есть планеты.
Земля вращается вокруг Солнца.
Земля планета.
Теперь эти силлогизмы можно проанализировать обычным образом.
Легко видеть, что первый силлогизм построен по II фигуре, для которой требуется, чтобы одна из посылок была отрицательной.
В этом силлогизме нет отрицательной посылки, поэтому вывод не следует.
Второй силлогизм, как можно заметить, построен по I фигуре.
Но и здесь нарушено правило фигуры.
От силлогизма I фигуры требуется, чтобы большая посылка в нём была общим суждением, но истинным будет только частное суждение.
Таким Образом, данная нам энтимема неверна: вывод не вытекает из посылок.
Может быть, кто-то выразит удивление: "Разве Земля не планета?" "Да, Земля - планета!"
И вывод здесь является истинным суждением.
Но дело в том, что он не вытекает из данных посылок.
Это бывает часто: когда выводное суждение представляется истинным, то кажется, что и умозаключение должно быть правильным. Однако это далеко не так.
Суждение должно быть истинным, но его обоснование с помощью умозаключения может оказаться ошибочным.
Итак, мы рассмотрели простой категорический силлогизм и его сокращенную форму – энтимему.
В наших реальных рассуждениях мы, конечно, не ограничиваемся этими простыми формами. Силлогизмы можно соединять в цепи, делая вывод одного силлогизма посылкой другого, а вывод второго – посылкой третьего и т.д.
Такие цепи силлогизмов называются полисиллогизмами.
Часто для краткости и компактности рассуждений мы опускаем в полиселлогизме отдельные посылки- такой сокращенный полисиллогизм называется соритом.
Например:
Допустим, надо доказать , что тайное присвоение книги из библиотеки общественно опасно.
Для этого построим следующую последовательность силлогизмов:
Все преступления общественно опасны!
Все хищения- преступления.
Все хищения общественно опасны.
Все хищения общественно опасны!
Все кражи- хищения. Все кражи общественно опасны.
Все кражи общественно опасны!
Все тайные присвоения книг из библиотеки - кражи.
Все тайные присвоения книг из библиотеки общественно опасны.
Например:
Все преступления общественно опасны.
Все хищения-преступления.
Все кражи – хищения.
Все тайные присвоения книг из библиотеки - кражи.
Все тайные присвоения книг из библиотеки общественно опасны!
Короче говоря, в повседневных рассуждениях мы можем самыми разнообразными способами комбинировать силлогизмы и энтимемы.
Однако, в основе всех этих комбинаций лежит та фундаментальная форма мысли, которую мы с вами подробно рассмотрели – простой категорический силлогизм.
Ниже приводятся силлогизмы и энтимемы.
Попробуйте проанализировать их корректность!
Сделайте вывод из посылок, восстановите энтимему в полный силлогизм, проверьте выполнение общих правил, определите фигуру силлогизма. Выполняет ли он правила сответствующей фигуры.
Сделайте хотя бы 5-7-10 примеров.
Может быть это занятие покажется вам скучноватым.
Но, к сожалению, только таким путем можно развить в себе способность делать выводы!
Когда вы смотрите по телевизору рекламу и какая-нибудь девица с фальшивой улыбкой убеждает вас: «Купите накладные волосы и вы будете счастливы!»
Умеете ли вы распознать здесь энтимему?
А это энтимема, и как только вы восстановите невысказанную посылку: «Каждый, купивший накладные волосы, счастлив», вы сразу же увидите, что она ложна.
39. Метод – это способ построения системы знания, совокупность приемов и операций теоретического и практического освоения действительности.
Современная система методов столь же разнообразна, как и сама наука. Различают экспериментальные, теоретические, эвристические и алгоритмические методы. Можно выделить количественные и качественные методы изучения реальности. В зависимости от степени обоснованности можно выделить статистические, вероятностные, гипотико-индуктивные и дедуктивные методы. Исходя из механизма обобщения рассматривают синтетические и аналитические, индуктивные и дедуктивные методы, методы идеализации, обобщения, типо-логизации и классификации.
Каждый из этих методов конкретизируется в какой-либо науке и наполняется своим конкретным содержанием. Некоторые методы являются универсальными, другие более ограничены. Например, эмпирический метод. Он заключается в накоплении, описании, объяснении, классификации и систематизации фактов и данныхэкспериментов над явлениями. Будучи конкретным, он далек от универсальности.
Перейдем к рассмотрению некоторых методов, используемых в логике.
Прежде всего это эвристический метод. Он представляет собой нахождение некоторого алгоритма решения проблемы. Здесь начинают играть существенную роль методы познания, связанные с математикой. В то же время данный метод, хотя и является теоретическим, тесно связан с эмпирическими методами построения теорий.
Более эффективным в логике является использование аксиоматического метода. Это способ построения теории, при котором некоторые положения теории выбираются в качестве исходных, а все остальные ее положения выводятся из них чисто логическим путем с помощью доказательств. Исходные положения называются аксиомами, а положения, доказываемые на их основе, – теоремами. Далее формулируется система правил, позволяющая преобразовывать исходные положения и из ограниченного числа аксиом получать множество доказуемых положений – теорем.
Одним из важных методов логики является метод формализации. Этот метод основывается на различении естественных и искусственных языков. Естественные языки складываются в процессе коммуникации и служат средством общения, передачи информации, выражения эмоций и т. д. В отличие от них, искусственные языки ориентированы на строго определенные и ограниченные задачи исследования. Они претендуют не только на сокращение записи, но и на более эффективную работу. Над формулами искусственных языков можно проводить операции, получать из них новые формулы и отношения. Символическое исчисление становится аналогом рассуждения, позволяющим дедуктивным образом из одних структур знаков и символов получать другие, выражающие новое знание о данном объекте.
Между структурами мышления и структурами их языкового выражения существует определенное соответствие. Это приводит к тому, что внутри формальной логики операции с мыслями о предметах можно заменить действиями со знаками и символами. Следовательно, формализация в данном случае представляет собой логический метод уточнения содержания мысли посредством уточнения ее логической формы.
40.
Индуктивное умозаключение — метод рассуждения от частного к общему.
Математическая индукция — метод доказательства для последовательности натуральных чисел либо объектов, однозначно занумерованных натуральными числами.
Полная индукция — метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности.
Неполная индукция — наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве.
Индукция (от лат. inductio — выведение) — процесс логического вывода на основании перехода от частных положений к общим. Среди наиболее важных законов индукции выступают правила доказательства, связывающие причину и следствие:
всегда, когда возникает причина, возникает и феномен (следствие);
всегда, когда есть феномен (следствие), ему предшествует причина;
если варьирует причина, варьирует и феномен;
если причина имеет дополнительные свойства, то и феномен приобретает дополнительные свойства.
Термин индукция впервые встречается у Сократа. Но индукция Сократа имеет мало общего с современной индукцией. Сократ под индукцией подразумевает нахождение общего определения понятия путём сравнения частных случаев и исключения ложных, слишком узких определений.
Индукция — это когда от отдельных случаев мы переходим к общему суждению. Индукция — это умозаключение, дающее вероятное суждение. Полная индукция — это такое умозаключение, когда общее заключение о всех элементах данного класса делается на основании рассмотрения каждого элемента этого класса. Полная индукция дает достоверное заключение, поэтому она применяется в математических и иных строгих доказательствах. Неполная индукция — это когда мы рассматриваем не все случаи изучаемого явления, а заключение делаем для всех.
Первый вид — индукция через простое перечисление — на основании повторяемости одного и того же признака у ряда однородных предметов и отсутствия противоречащего случая делается общее заключение, что все предметы этого рода обладают этим признаком. Пример: считали, что все лебеди белые, пока не встретили черного лебедя.
Второй вид — индукция через анализ и отбор фактов — стремление исключить случайность обобщений, т. к. изучаются планомерно отобранные и наиболее типичные предметы разнообразные по времени, способу получения и т. д. Пример: для определения качества рыбных консервов берут банки из разных партий и разных холодильников.
Третий вид — научная индукция — это умозаключение, в котором на основании познания необходимых признаков делается общее заключение обо всех предметах данного класса. Дает достоверный вывод, опирается на всесторонность анализа фактов.
Психология изучает развитие и нарушения индуктивных рассуждений. Движение от единичного к общему знанию анализируется в его обусловленности всеми психическими процессами, строением мыслительной деятельности в целом. Примером экспериментальных исследований индуктивных рассуждений являются опыты с образованием искусственных понятий.
Индукция – это умозаключение от знания меньшей степени общности к новому знанию большей степени общности.
Посылками индуктивного умозаключения являются суждения, в которых закрепляется информация, полученная опытным путем, об устойчивости признака у ряда явлений, принадлежащих одному и тому же классу.
Основной функцией индукции является генерализация, т. е. получение общих суждений. Данные обобщения могут носить различный характер – от простейших до эмпирических.
Общее, существенное, повторяющееся и закономерное в предметах познается через изучение отдельного, и одним из средств познания общего выступает индукция. В зависимости от избранного основания выделяют два вида индуктивных умозаключений: полную и неполную индукцию.
Полная индукция – это умозаключение, в котором общее заключение о всех элементах класса предметов делается на основании рассмотрения каждого элемента этого класса.
Данные индуктивные умозаключения применяются в тех случаях, когда имеется дело с замкнутыми классами, в которых число элементов конечно и которые легко обозримы (например, число планет Солнечной системы).
Заключение по полной индукции может быть сделано не только из единичных, но и из общих суждений. Она дает достоверное заключение, поэтому ее часто применяют в математике и в других строгих доказательствах.
Неполная индукция – это умозаключение, в котором при повторяемости признаков у явлений опреде-. ленного класса делают вывод о принадлежности этого признака всему классу явлений.
Неполная индукция применяется в тех случаях, когда нельзя рассмотреть все интересующие элементы явлений; если число объектов либо бесконечно, либо конечно, но достаточно велико; рассмотрение уничтожает объект. При данном виде индукции исследуются не все, а некоторые элементы класса, и если у каждого из них обнаруживается повторяющийся признак, то делают вывод о его принадлежности всему классу явлений.
Одним из видов неполной индукции является научная индукция. Научной индукцией называется такое умозаключение, в котором на основании познания необходимых признаков или необходимой связи части предметов класса делается общее заключение обо всех предметах этого класса. Научная индукция так же, как полная и математическая, дает достоверное заключение.
Научная индукция опирается не столько на большое число исследованных фактов, сколько на всесторонность их анализа и установление причинной зависимости, выделение необходимых признаков или необходимых связей, предметов и явлений. Поэтому она и дает научное заключение.
Научная индукция в посылках опирается только на существенные связи и отношения, благодаря чему достоверность ее заключений носит необходимый характер.
Другим видом неполной индукции является популярная индукция. На основании повторяемости одного и того же признака у ряда однородных предметов и отсутствия противоречащего случая делается общее заключение, что все предметы этого рода обладают этим признаком. Такая индукция дает заключение вероятное, а не достоверное.
41. Методы научной индукции - это методы установления причинных связей между явлениями. Это довольно простые и часто применяемые в повседневной практике методы. Впервые они были описаны английским философом Ф. Бэконом, а затем систематизированы и усовершенствованы другим английским ученым Дж. Миллем. Существует пять методов научной индукции.
1. Метод сходства состоит в том, что если два и более случаев, каждый из которых вызывает исследуемое явление, имеют какое-либо одно - единственное общее обстоятельство, то это общее обстоятельство является, вероятно, причиной искомого явления. Схема:
При обстоятельствах А, В, С происходит явление d.
При обстоятельствах М, F, В происходит явление d.
При обстоятельствах М, В, С происходит явление d.
По-видимому, обстоятельство В является причиной d.
Например, наблюдая случаи дорожно-транспортных происшествий (в разное время суток, разных марок машин, различий в возрасте водителей и т. д.), можно сделать заключение, что большинство из них происходит в результате превышения скорости или алкогольного опьянения водителей.
2. Метод различия - метод, основанный на сравнении двух случаев, в одном из которых исследуемое явление наступает, а в другом - не наступает и при этом первый случай отличается от второго только одним обстоятельством; вероятно, именно это обстоятельство является причиной исследуемого явления. Схема:
При обстоятельствах А, В, С происходит явление d.
При обстоятельствах В, С не происходит явление d.
Вероятно, обстоятельство А является причиной d.
Например, в исследуемых случаях совершения кражи на предприятии установлено, что в тех случаях, когда кражи не было, отсутствовал по разным причинам один из работников охраны предприятия. Можно сделать предположение, что именно этот человек осуществлял кражу.
3. Объединенный метод сходства и различия представляет собой комбинацию первых двух методов, когда путем анализа множества случаев обнаруживают в них как сходное, так и различное. Исследование причинных связей по данному методу осуществляется по следующей схеме:
При обстоятельствах А, В, С происходит явление d.
При обстоятельствах А, Д, Е происходит явление d.
При обстоятельствах В, С не происходит явление d.
При обстоятельствах Д, Е не происходит явление d.
Вероятно, А является причиной d.
Вероятность заключения в таком рассуждении увеличивается, так как соединяются преимущества и метода сходства, и метода различия.
4. Метод сопутствующих изменений используется при анализе сходных случаев, когда изменение одного обстоятельства всякий раз сопровождается изменением другого обстоятельства. На этом основании делается вывод о причинной связи между двумя меняющимися обстоятельствами.
Например, увеличение трения приводит к уменьшению скорости движения тела. Следовательно, причиной изменения скорости движения тела является увеличение трения. Или: чем хуже состояние дороги, тем больше совершается дорожно-транспортных происшествий (при прочих равных условиях). Чем лучше состояние дороги, тем меньше происшествий. По-видимому, состояние дороги может рассматриваться как одна из причин дорожно-транспортных происшествий.
Исследование по данному методу осуществляется по следующей схеме:
При обстоятельствах А, В, С происходит явление d.
При обстоятельствах А1, В, С происходит явление d1.
При обстоятельствах А2, В, С происходит явление d2.
По-видимому, обстоятельство А является причиной d.
Степень вероятности заключения по данному методу зависит от числа рассмотренных случаев, от точности знания о предшествующих обстоятельствах, а также от адекватности изменений предшествующего обстоятельства и исследуемого явления. Нужно также иметь в виду, что для исследователя интерес представляют не любые, а лишь пропорционально нарастающие или убывающие изменения. Недостатком этого метода является то, что он не позволяет выяснить вопрос о том, какова в каждом случае причинная связь. Может быть так, что взаимоизменяющиеся обстоятельства А и явление d - следствие какой-то общей для них причины.
5. Метод остатков связан с установлением причины, вызывающей определенную часть сложного следствия, когда причины остальных частей этого следствия уже установлены. Схема метода:
При обстоятельствах А, В, С происходит сложное явление а, b, с.
Обстоятельство А вызывает часть явления - а.
Обстоятельство В вызывает часть явления - b.
Вероятно, обстоятельство С является причиной явления с.
Эта схема иллюстрирует следующее правило метода остатков: если вычесть из данного явления ту часть его, о которой известно, что она есть следствие определенных предшествующих обстоятельств, то остающаяся часть (остаток) явления будет следствием остальных предшествующих обстоятельств.
При помощи этого метода была открыта планета Нептун.
Особым видом умозаключений неполной индукции является статистическая индукция, или статистическое обобщение.
Статистическое обобщение - это умозаключение неполной индукции, в котором содержится количественная информация о частоте распределения некоторого признака для определенного класса предметов. Этот класс называется популяцией, а любой подкласс из популяции - образцом, выборкой или пробой. Таким образом, статическая индукция - умозаключение от образца к популяции.
Так, статистическая информация о совершении преступлений такого рода, как хулиганство, показывает, что из 100 случаев хулиганских действий до 95 из них совершаются в состоянии алкогольного опьянения. Значит, частота хулиганства, сопровождаемого алкогольным опьянением, определяется как 95:100, т.е. равна 95%.
В статистических обобщениях логический переход от посылок к заключению дает лишь правдоподобное или вероятное заключение
Степень вероятности заключения, полученного с помощью неполной индукции, повышается при:
Ø увеличении числа предметов исследуемого класса;
Ø исследовании как можно более разнообразных видов предметов данного класса;
Ø обобщении предметов по наиболее существенным признакам, характеризующим предметы исследуемого класса;
Ø раскрытии причины появления и изменения предметов исследуемого класса;
Ø сопоставлении полученных заключений с другими положениями науки в данной области знания, законами, дополнении их с дедуктивными умозаключениями.
Индуктивные умозаключения представляют собой логические процедуры, с помощью которых обобщаются результаты опытных исследований. История науки показывает, что многие научные открытия были сделаны на основе индуктивного обобщения эмпирических (опытных) данных. Важное место занимают индуктивные умозаключения в судебно-следственной практике. На их основе формулируются многочисленные обобщения, касающиеся обычных отношений между людьми, мотивов и целей совершения преступлений, способов их совершения, типичных реакций виновников преступлений на действия следственных органов и т. п.
Индуктивные умозаключения в расследовании преступлений имеют свои особенности. Во-первых, результатом обобщения являются не законы, как в научной индукции, а знание сложного единичного события. Во-вторых, обобщаются не только однородные предметы и явления, но и разнородные (например, если совершена кража, то систематизируются способы проникновения преступников в помещение, объект посягательства, количество похищенного и т. д.). Это осложняет индукцию, вводит в нее дополнительные приемы и условия построения умозаключений.
Индукция и дедукция - два взаимосвязанных вида умственных действий, два метода исследования. Общие положения, используемые в дедукции, представляют собой результат предварительного индуктивного обобщения некоторой совокупности фактов, данных научных наблюдений. Например, используемые в дедуктивных умозаключениях большие посылки составляются на основе «индукции» из человеческого опыта или на основе знаний, почерпнутых из специальных наук. Индуктивные умозаключения расширяют наши знания путем распространения известного на неизвестные явления, устанавливают общие правила, законы, причинно-следственные связи, лежат в основе построения гипотез (следственных версий).
Полученные с помощью индукции обобщения играют важную эвристическую роль: они становятся первоначальными предположениями, догадками или гипотетическими объяснениями, которые затем проверяются и уточняются.
Взаимосвязь индукции и дедукции обеспечивает логическую направленность и обоснованность заключений. Если мы вспомним знаменитых сыщиков, описанных в детективной литературе (например, Дюпена, Шерлока Холмса, Пуаро), то обратим внимание на то, что они преуспевали в расследовании преступлений именно благодаря наблюдательности и аналитическим способностям (индукции и дедукции). С удивительной точностью и умением они отыскивали причины, побудившие человека к тому или иному преступлению, и с математической точностью делали соответствующие выводы; из незначительных следов, побочных обстоятельств делали остроумные выводы, восстанавливая картину преступления.
И в обыденной жизни они умели «наблюдать» за всеми, с кем им приходилось встречаться, замечая форму рук, ногтей, наличие мозолей на руках, особенности выражения лица, манеру держаться и т. п. В одежде обращали внимание на платья, манжеты, брюки - пятна и потертости на них наводили сыщиков на остроумные заключения относительно происхождения, образа жизни, привычек, прошлого и многих других обстоятельств жизни данного человека. Забытый преступником предмет, например перчатка, шляпа и даже окурок сигары, давали возможность прийти к умозаключениям, из которых нередко создавалось полное описание личности преступника.
В науке и практических делах объектом исследования нередко выступают единичные, неповторимые по своим индивидуальным характеристикам, события, предметы и явления. При их объяснении и оценке затруднено применение как дедуктивных, так и индуктивных рассуждений. В этом случае прибегают к третьему способу рассуждения - умозаключению по аналогии.
42 1. Понятие аналогии
В науке и практических делах объектом исследования нередко выступают единичные, неповторимые по своим индивидуальным характеристикам события, предметы и явления. При их объяснении и оценке затруднено применение как дедуктивных, так и индуктивных рассуждений. В этом случае прибегают к третьему способу рассуждения —умозаключению по аналогии: уподобляют новое единичное явление другому, известному и сходному с ним единичному явлению и распространяют на первое ранее полученную информацию.
Например в истории физики, когда при выяснении механизма распространения звука его уподобили движению жидкости. На основе этого уподобления возникла волновая теория звука. Объектами уподобления в этом случае были жидкость и звук, а переносимым признаком — волновой способ их распространения.
Умозаключение по аналогии — это вывод о принадлежности определенного признака исследуемому единичному объекту (предмету, событию, отношению или классу) на основе его сходства в существенных чертах с другим уже известным единичным объектом.
Умозаключению по аналогии всегда предшествует операция сравнения двух объектов, которая позволяет установить сходства и различия между ними. При этом для аналогии требуются не любые совпадения, а сходства в существенных признаках при несущественности различий. Именно такие сходства служат основой кля уподобления двух материальных или идеальных объектов.
Логический переход от известного к новому знанию регулируется в выводах по аналогии следующим правилом: если два единичных предмета сходны в определенных признаках, то они могут быть сходны и в других, обнаруженных в одном из сравниваемых предметов, признаках.
