
- •1.Векторы. Основные операции над векторами.
- •4.Простейшие задачи на плоскости.
- •6. Угол между прямыми. Условия перпендикулярности и параллельности прямых.
- •2.Базис. Разложение вектора по базису.
- •20.Ранг матрицы.
- •3.Скалярное произведение 2-х векторов и его свойства.
- •5.Различные уравнения прямой.
- •1.Общее уравнение прямой:
- •2.Каноническое уравнение прямой:
- •9.Гипербола.
- •7.Общее уравнение кривой. Кривые второго порядка.
- •3)Если:
- •8.Эллипс.
- •15.Метод Крамера.
- •10.Парабола.
- •11.Уравнение плоскости.
- •14.Свойства определителей.
- •18.Матричная запись системы. Применение
- •19.Решение систем линейных уравнений методом Гаусса.
- •21.Теорема Кронекера- Капелли. Решение неопределенных
5.Различные уравнения прямой.
1.Общее уравнение прямой:
2.Каноническое уравнение прямой:

 k=tgα
k=tgα
y-B=kx
y=kx+B
3.Ур-е пучка прямых, проходящих через заданную точку:
 y=kx+b
y=kx+b


y=kx+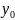 -k
-k
y- =kx-k
4.Ур-е прямой. проходящей через 2 заданные точки:
y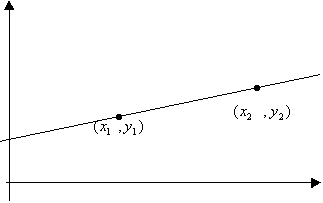 -
=k(x-
)
-
=k(x-
)
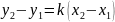
k=
y-
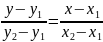
9.Гипербола.
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от
которых до двух заданных точек F1 (с;0)и F2 (-с;0), называемых фокусами гиперболы, есть вели-
чина постоянная =2а.
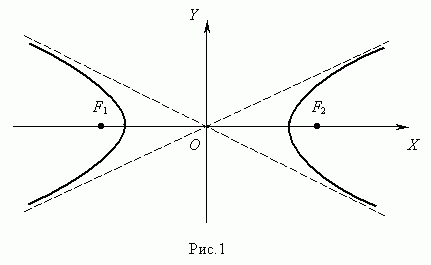
Здесь начало координат является центром симметрии гипер-
болы, а оси
координат – её осями симметрии.
Отрезок F1F2 =
2 с ,
где , c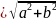 называется фокусным
расстоянием.
Отрезок AB =
2 a называется действительной
осью гиперболы,
а отрезок CD =
2 b – мнимой
осью гиперболы.
называется фокусным
расстоянием.
Отрезок AB =
2 a называется действительной
осью гиперболы,
а отрезок CD =
2 b – мнимой
осью гиперболы.
Число 𝛏= c / a , e > называется эксцентриситетом гиперболы. Прямые y = ± ( b / a ) x называются
асимптотами
гиперболы.
Прямые х= называются директрисами
гиперболы.
называются директрисами
гиперболы.
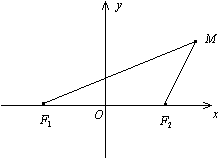 Уравнение
гиперболы :
Уравнение
гиперболы :

Доказательство:
![]()
![]()
![]()
7.Общее уравнение кривой. Кривые второго порядка.
Ax2+Bxy+Cy2+Dx+Ey+F=0
если B=0,то кривые наз-ся центрально симметричными.
Ур-е
имеет вид:
![]()
Рассматривается произведение А×С
Если ,А×С˃0, то эллипс;
Если А×С˂0, то гипербола;
Если А×С=0 , то парабола.
Выделяем полный квадрат уравнения
получим:
![]() или
или
![]()
,
обозначим: ![]()
![]() ;
; ![]() .
.
1)Если А×С˃0 , то уравнение задает кривую эллиптического типа. Причем:
![]() -
мнимый
эллипс.
-
мнимый
эллипс.
![]() -
точка
-
точка ![]() .
.
![]() ,
то имеем
,
то имеем ![]() -
канонический
вид эллипса.
-
канонический
вид эллипса.
2)Если А×С˂0, то уравнение задает кривую гиперболического типа. Причем:
Если ![]() ,
или
,
или ![]() имеем:
имеем:
![]() или
или ![]() - канонический
вид гиперболы.
- канонический
вид гиперболы.
Если ![]() и
учитывая знаки А и С
имеем:
и
учитывая знаки А и С
имеем:
![]() - пара
пересекающихся прямых(вырожденная
гипербола)
- пара
пересекающихся прямых(вырожденная
гипербола)
3)Если:
С=0 ,
то общее уравнение ![]() задает
кривую параболического типа. Выделяя
полный квадрат имеем:
задает
кривую параболического типа. Выделяя
полный квадрат имеем:
![]() .Обозначим:
.Обозначим: ![]() имеем:
имеем:
![]() -
канонический
вид параболы.
-
канонический
вид параболы.
А=0 ,
то ![]() -
кривая параболического типа. Выделяя
полный квадрат имеем:
-
кривая параболического типа. Выделяя
полный квадрат имеем:
![]() .Обозначим:
.Обозначим: ![]() -
имеем:
-
имеем:
![]() -
канонический
вид параболы.
-
канонический
вид параболы.
8.Эллипс.
Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух
з аданных
точек F1
(с;0) и
F2
(-с;0),
называемых фокусами эллипса,
есть величина постоянная = 2а.
аданных
точек F1
(с;0) и
F2
(-с;0),
называемых фокусами эллипса,
есть величина постоянная = 2а.
Здесь начало координат является центром симметрии эллипса,
а оси координат – его осями симметрии. При a > b фокусы
эллипса лежат на оси ОХ , при a < b фокусы эллипса лежат на
оси ОY , а при a = b эллипс становится окружностью. Таким
образом, окружность есть частный случай эллипса. Отрезок
F1F2 =
2 с ,
где ,
называется
фокусным
рассто
,
называется
фокусным
рассто
янием. Отрезок AB = 2 a называется большой осью эллипса, а
отрезок CD =
2 b – малой
осью эллипса.
Число 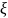 = c / a , e <
1
= c / a , e <
1
называется эксцентриситетом эллипса.
Число х= называется директрисой эллипса.
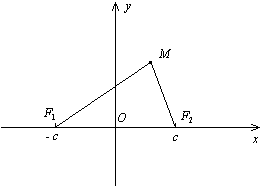 Уравнение
эллипса :
Уравнение
эллипса : +
+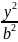 =1,
b=
=1,
b=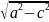
Доказательство. Пусть М(x;y) -- текущая точка эллипса. По определению эллипса F1M+F2M=2a.
Фокусами в выбранной системе координат являются точки F1(-c;0),F2(c;0) . Находим
![]()
Тогда по определению эллипса
![]()
![]()
![]()
![]()
![]()
Учитывая, что b2=a2-c2, имеем равенство x2b2+y2a2=a2b2
Наконец, разделив обе части на a2b2 , получим уравнение + =1
