Математичні моделі економічних задач

Математична модель задачі – це відображення оригінала у вигляді функцій, рівнянь, нерівностей. Математична модель включає: 1) сукупність невідомих величин , які називають планом задачі; 2) цільову функцію (функцію цілі, показника ефективності, критерій оптимальності); 3) умови (або систему обмежень), яким підпорядковуються невідомі величини. Їх сукупність утворює область допустимих розв’язків (область економічних можливостей).

Задача. На дільниці цеху виготовляють деталі двох найменувань А і В за допомогою двох операцій на токарному та фрезерувальному верстатах. Витрати часу на обробку однієї деталі на кожному з верстатів у годинах подано у таблиці.

Верстат	Деталі
	А	В
Токарний	0,25	0,1
Фрезерувальний	0,15	0,3

За планом деталей А необхідно виготовити не менше як 500 одиниць за місяць, а деталей В – не менше як 210 одиниць. Скласти найкращу програму (план) оптимального використання обладнання, коли відомо, що фонд часу (тривалість роботи) кожного з верстатів становить відповідно 180 годин за місяць для токарного верстата і 170 годин для фрезерувального.

Розв’язання. Будемо вважати, що деталей А треба виготовити одиниць, а деталей В – одиниць. На обробку запланованих деталей на токарному верстаті доведеться витратити таку кількість годин: деталей А – 0,25 годин і деталей В – 0,1 годин, але сума цього часу не може перевищити 180 годин, тобто

Для фрезерувального верстата на обробку деталей може піти не більше 170 годин, тобто

За планом деталей А треба виготовити не менше як 500 одиниць, тобто а деталей В не менше як 210 одиниць –

Задача виробництва полягає в тому, щоб не перевищити фонд часу кожного з верстатів, виконати план і випустити найбільшу загальну кількість продукції. Позначимо загальну кількість продукції буквою тоді

Одержали таку математичну модель задачі:

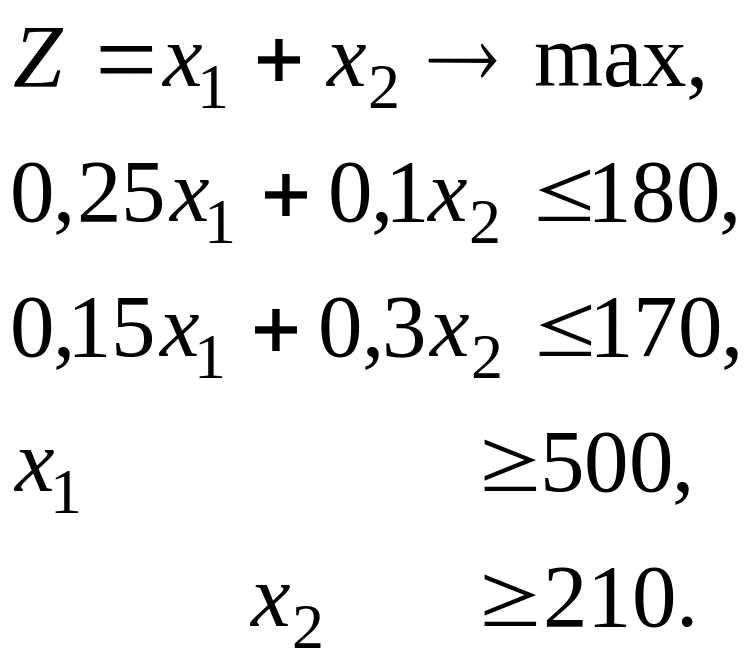
Невід’ємність змінних і випливає з умови задачі.

Основні поняття математичного програмування

Математичне програмування – це наука про методи дослідження на екстремум та найбільше значення функції багатьох змінних, на невідомі якої накладено обмеження (умовний екстремум).

Цільовою називають функцію, оптимальне значення якої шукають.

Якщо цільова функція і система обмежень лінійні, то задача математичного програмування є задачею лінійного програмування.

Допустимим розв’язком (планом) задачі лінійного програмування називається будь-який п-мірний вектор , що задовольняє системі обмежень і умовам невід’ємності.

Оптимальним розв’язком (планом) задачі лінійного програмування називається такий допустимий розв’язок (план) задачі, при якому цільова функція досягає екстремуму.

Форми записів задач лінійного програмування (ЗЛП)

1. Канонічна форма запису ЗЛП

– цільова функція.

(1)

2. Симетричні форми запису ЗЛП:

,

(2)