
- •1. Нормальний вектор прямої. Рівняння прямої, яка проходить через задану точку перпендикулярно заданому вектору
- •2. Загальне рівняння прямої
- •3. Точка перетину прямих. Побудова прямої за допомогою
- •4. Напрямний вектор прямої. Канонічне рівняння прямої
- •5. Рівняння прямої, яка проходить через задану точку в заданому
- •7. Рівняння прямої, яка проходить через дві точки
- •8. Рівняння прямої у відрізках
- •10. Віддаль від точки до прямої
7. Рівняння прямої, яка проходить через дві точки
Рис.



 Нехай
задано дві точки М1(х1,у1)
і М2(х2,у2).
Рівняння прямої, що проходить через ці
дві точки, запишемо як рівняння прямої,
яка проходить через точку
Нехай
задано дві точки М1(х1,у1)
і М2(х2,у2).
Рівняння прямої, що проходить через ці
дві точки, запишемо як рівняння прямої,
яка проходить через точку
![]() паралельно вектору
паралельно вектору
![]() ,
який візьмемо за напрямний вектор
.
Тобто, вектор
,
який візьмемо за напрямний вектор
.
Тобто, вектор
![]() .
Якщо М(х,у) –
довільна точка на прямій l,
то вектор
.
Якщо М(х,у) –
довільна точка на прямій l,
то вектор
![]() колінеарний вектору
.
Тоді канонічне рівняння прямої матиме
вигляд:
колінеарний вектору
.
Тоді канонічне рівняння прямої матиме
вигляд:
![]() . (12)
. (12)
Це і є рівняння прямої, яка проходить через дві задані точки.
8. Рівняння прямої у відрізках
Рис.

 Нехай
пряму l
задано
за допомогою двох відрізків, які вона
відтинає на осях Ох
і Оу.
Позначимо відрізки, які відтинає ця
пряма на осях Ох
і Оу,
відповідно через a
і b.
(рис. ). Тоді матимемо дві точки
Нехай
пряму l
задано
за допомогою двох відрізків, які вона
відтинає на осях Ох
і Оу.
Позначимо відрізки, які відтинає ця
пряма на осях Ох
і Оу,
відповідно через a
і b.
(рис. ). Тоді матимемо дві точки
![]() і
.
Запишемо рівняння прямої, що проходить
через дві точки А
і В:
і
.
Запишемо рівняння прямої, що проходить
через дві точки А
і В:
![]() ,
або
,
або
![]() ,
або
,
або
![]() (13)
(13)
Рівняння (13) і є рівнянням прямої у відрізках на осях.
9. Обчислення кута між двома прямими. Умова паралельності і перпендикулярності двох прямих
Рис.
 l1:
l1:
![]()
l2:
![]()


 Нормальним
вектором прямої l1
буде вектор
Нормальним
вектором прямої l1
буде вектор
![]() ,
а прямої l2
– вектор
,
а прямої l2
– вектор
![]() .
.
Кут
між векторами
![]() і
і
![]() (рис. ) дорівнює одному з кутів між прямими
l1
i
l2.
(рис. ) дорівнює одному з кутів між прямими
l1
i
l2.
Тоді
 . (14)
. (14)
Умова
паралельності
двох прямих
випливає з формули (14), якщо покласти
![]() або
або
![]() ,
або з умови колінеарності векторів
і
.
Тоді маємо
,
або з умови колінеарності векторів
і
.
Тоді маємо
![]() . (15)
. (15)
Умова
перпендикулярності
двох прямих
випливає з формули (14), якщо покласти
![]() або
або
![]() (
(![]() ),
або з умови перпендикулярності векторів
і
.
Тоді маємо
),
або з умови перпендикулярності векторів
і
.
Тоді маємо
![]() .
(16)
.
(16)
20. Прямі задано канонічними рівняннями. Нехай прямі l1 i l2 задано рівняннями:
l
Рис.
 1:
1:
![]()

 l2:
l2:
![]()
Напрямний
вектор прямої l1
є вектор
![]() ,
а прямої l2
– вектор
,
а прямої l2
– вектор
![]() .
Кут між двома прямими можна вимірювати
кутом між їхніми напрямними векторами
(рис. ).
.
Кут між двома прямими можна вимірювати
кутом між їхніми напрямними векторами
(рис. ).
Тоді
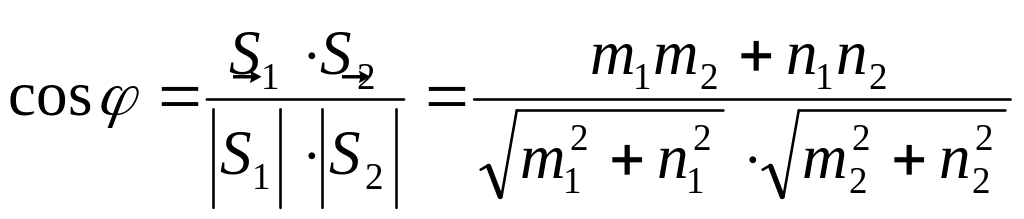 . (17)
. (17)
Якщо прямі
l1
i
l2
паралельні, то вектори
![]() і
і
![]() колінеарні,
отже, їхні координати пропорційні,
колінеарні,
отже, їхні координати пропорційні,
![]() – умова
паралельності двох прямих. (18)
– умова
паралельності двох прямих. (18)
Якщо прямі l1 i l2 перпендикулярні, то їхні напрямні вектори і також перпендикулярні, отже, їхній скалярний добуток дорівнює нулю
![]() – умова
перпендикулярності. (19)
– умова
перпендикулярності. (19)
3
Рис.

 0.
Прямі задано рівняннями з кутовими
коефіцієнтами. Нехай
дві прямі l1
i
l2,
які перетинаються в точці М задано
рівняннями:
0.
Прямі задано рівняннями з кутовими
коефіцієнтами. Нехай
дві прямі l1
i
l2,
які перетинаються в точці М задано
рівняннями:
l1: у=k1x+b1,
l2: y= k2x+b2.
 Знайдемо
тангенс кута між цими прямими. Нехай
дві прямі не перпендикулярні між собою.
Інакше tg
Знайдемо
тангенс кута між цими прямими. Нехай
дві прямі не перпендикулярні між собою.
Інакше tg![]() –
не існує. З рис. видно, що
=
–
не існує. З рис. видно, що
=![]() Тоді
Тоді
![]() . (20)
. (20)
Але
![]() ,
,
![]() ,
тому
,
тому
![]()
Якщо дві
прямі паралельні або співпадають, то
![]() отже
отже
![]() ,
,
![]() . (21)
. (21)
І навпаки, якщо k1=k2, то прямі паралельні.
Умова (14) є необхідною і достатньою мовою паралельності двох прямих.
Якщо прямі перпендикулярні, то формула (20) не має змісту. Але тоді
![]()
У випадку
перпендикулярності
![]() .
Звідки
.
Звідки ![]() або 1+k1k2=0
, або
або 1+k1k2=0
, або
![]() ,
,
![]() (22)
(22)
Можна показати, що формула (22) є необхідною і достатньою умовою перпендикулярності двох прямих.
