Пряма лінія на площині

1. Нормальний вектор прямої. Рівняння прямої, яка проходить через задану точку перпендикулярно заданому вектору

Нехай на площині xОy задано деяку точку і вектор перпендикулярний до l (рис.1).

y

l

M

M₀

O x

Рис. 1

Вектор називається нормальним вектором прямої. Точка і вектор однозначно визначають положення прямої на площині. Нехай М(x,y) – довільна точка на прямій l. За умовою вектор і вектор перпендикулярні. Тому скалярний добуток .

Таким чином, ми дістали рівняння

, (1)

якому задовольняє будь–яка точка М(x,y) є l.

Рівняння (1) називається рівнянням прямої, яка проходить через задану точку перпендикулярно заданому вектору.

2. Загальне рівняння прямої

З формули (1) видно, що рівняння прямої є лінійним відносно поточних координат x i y.

Покажемо, що і, навпаки, будь–яке рівняння першого степеня

Аx+By+C=0 (2)

відносно координат x i y є рівняння деякої прямої, яка лежить в площині Oxy.

Дійсно, нехай в (2) хоча б один із коефіцієнтів А або B відмінні від нуля (інакше дістанемо тотожність C=0). Нехай, наприклад, В 0. Тоді рівняння (2) рівносильне рівнянню

(3)

Але останнє є рівнянням прямої, яка проходить через точку з координатами перпендикулярно вектору , якщо С=0, то рівняння (2) має вигляд Аx+By=0 i йому задовольняють координати x=0, y=0. В цьому випадку пряма проходить через початок координат.

Легко бачити, що y=0 є рівнянням осі Оx, а х=0 – рівнянням осі Оy.

Дійсно, взявши нормальний вектор

і точку М₀(0,0), запишемо

р івняння прямої 0(x–0)+1(y–0)=0. y

Звідки одержуємо рівняння осі Ох: y=0.

А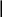 налогічно для осі Оу:

н ормальний вектор ,

точка М₁(0,0), рівняння прямої О M₀(0,0) x

1·(x–0)+0·(y–0)=0.

Звідки одержуємо рівняння осі Оу: x=0. Рис. 2

3. Точка перетину прямих. Побудова прямої за допомогою

її рівняння

Нехай задані дві прямі i i потрібно знайти їх точку перетину. Точка перетину повинна задовольняти обом рівняння. І тому її можна знайти, розв’язавши систему

(4)

Для побудови прямої достатньо знайти дві точки. Ці точки можемо знайти задавши довільним чином одну із координат, а потім з рівняння знайти другу. Якщо А 0 і В 0, то саме краще знайти точки перетину з осями координат.

Приклад. Побудувати пряму 3x+2y–6=0; у

Р озв’язання. Знайдемо координати двох точок: 3 М₂

1. п ри x=0; y=3;

2. п ри x=2; y=0.

З а двома точками: М₁(2,0) і М₂(0,3) М₁

побудуємо пряму (рис. 3). О 2 х

Рис. 3