
- •Вопрос 1 Предмет тв
- •Вопрос 2.Случайные события и их классификации.
- •Вопрос 3.Классическое, статистическое и геометрическое опр вероятности.
- •Вопрос 5.Теорема сложения вероятностей несовместных событий и ее следствия.
- •Вопрос 6.Зависимые и независимые события. Условная вероятность. Теоремы умножения вероятностей.
- •Вопрос 7 Вероятность появления хотя бы одного из n событий, независимых в совокупности.
- •Вопрос 8 Теорема сложения вероятностей совместных событий. Вероятность наступления только одного, хотя бы одного события
- •Вопрос 9 Формула полной вероятности и формула Байеса
- •Вопрос 10 Понятие дискретной случайной величины и ее з-на распределения. Многоугольник распределения.
- •Вопрос 12.Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа св х формулой:
- •Вопрос14.Повторные независимые испытания. Ф-ла Бернулли.
- •Вопрос 15.Биноминальное распределение
- •Вопрос 16.Закон Пуассона
- •Вопрос 17.Равномерной дискретное распределение
- •Вопрос18.Плотность распределения вероятностей непрерывной случайной величины и ее свойства.
- •Вопрос 20 равномерный закон распределения
- •Вопрос 22 Нормальный закон распределения, его параметры и их вероятностный смысл. Влияние параметров а и б на форму нормальной кривой.
- •Вопрос 27Нерав-во Маркова
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31 Понятие о центральной предельной теореме и ее следствиях.
- •Вопрос 32 Локальная и интегральная теоремы Лапласа как следствие теоремы Ляпунова.
- •Вопрос 32 Теорема Ляпунова
- •Вопрос 33 Предмет и задачи мат статистики, ген и выборочная совокупности, способ отбора.
- •Вопрос 34 Построение дискретного вариационного ряда. Эмпирическая ф-ия распределения.
- •Вопрос 35 Построение интервального вариационного ряда. Гистограмма частот.
- •Вопрос 36 Средняя арифметическая и ее свойства. Устойчивость выборочных средних
- •Вопрос 37 Дисперсия вариационного ряда и ее св-ва. Исправленная выборочная дисперсия.
- •Вопрос 41 Основные понятия стат проверки гипотез. Гипотезы h0 и h1, критерии проверки, ошибки первого и второго рода, критическая область, мощность критерия.
- •Вопрос 42 Проверка гипотезы о равенстве мат ожиданий 2ух нормально распределенных ген сов при известной дисперсии.
- •Вопрос 44Распределение Пирсона (или “хи”-квадрат распределение
Вопрос 22 Нормальный закон распределения, его параметры и их вероятностный смысл. Влияние параметров а и б на форму нормальной кривой.
Непрерывная с.в.Х
наз-ся распределенной по нормальному
з-ну с пар-ми a
и r
(где r>0),
если ее плотность имеет вид
![]() (1)
(1)
Если а=0 и r=1,
то нормальное распред-е наз=ся стандартным,
или нормальным. Для него p(x)=(x)=
![]() (2)
(2)

![]()
При любом заданном а и любом заданном r, гр. ф-ции (1) аналогичен гр-ку стандартной кривой (2) и обладает след. св-вами:
1 график симметричен относ-но прямой х=а
2 при изм-ии а и при пост r норм кривая, не изм-няя своей формы смещается вдоль оси ОХ.
3 при пост а, при увеличении r норм. кривая как бы расплющивается вдоль оси ОХ, а при уменьшении r-станов-ся шпилеобразной.
Вопрос 23 Вер-ть попадания нормально распределенной случ вел-ны в заданный интервал, вероятность заданного отклонения

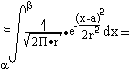

=




![]()
Вопрос 24
Правило 3-х
Полагая r получим:з(|x-a|<3r)=Ф(3r/r)=Ф(3)=0,9973
Правило:практически достоверным явл событие значения случ величины, распред-й по норм з-ну, содержатся в инт-ле (a-3r;a+3r).лишь в 27 случаях из 10тыс значения норм случ величины попадают в этот интервал.
На практике для
грубой оценки ср. квадр-ие отк-я пользуются
рав-вом :
![]()
Вопрос 25
Функцией Лапласа
называется
![]()
![]()
Свойства
1 Ф(-х)=-Ф(х) – нечетная
2
limx->+![]() Ф(х)=1[Ф(0)=0,Ф(1)=0,6827,Ф(2)=0,9545]
Ф(х)=1[Ф(0)=0,Ф(1)=0,6827,Ф(2)=0,9545]
Иногда ф-ю наз.
интегралом вероятностей. Можно д-ть,
что если х принадлежит r
(a;r),
то
![]()
Вопрос 26 Моменты случ вел-н. Ассиметрия и эксцесс.
Нач момента случ
величины х к-того порядка называют
число![]() ,
равное мат. отношению к-й степени случ
вел
,
равное мат. отношению к-й степени случ
вел
![]()
Если х-д.с.в., то
![]() .
Можно доп-ть,что знание всех начальных
моментов позволяет восстановить ф-цию
распределения F(x)
с.в. Х как наиболее обобщающей хар-ки.
.
Можно доп-ть,что знание всех начальных
моментов позволяет восстановить ф-цию
распределения F(x)
с.в. Х как наиболее обобщающей хар-ки.
Центр.момент к-того порядка Мк наз. математическим ожиданием к-ой степени отклонения случ.вел. от своего мат. ожидания.
Ассиметрией теоретического распред-я наз-ся отн-е центр. момента 3-го пор-ка к кубу ср. квадр. ожидания.
Для норм. распред-я и для всех др. симметрич-х относит-но (М(х)) расп-й Аs=0

As>0,
если «длинная часть» кривой распределения
нах-ся правее мат. ожид-я. В противном
случае As<0.
Для оценки крутости теоретич. Расп-я по
срав-ю с нормальн. кр-ой с теми же М(х) и
P(x)
примен-ся эксцесс, кот. Опр-ся так
![]() ,
для норм. зн-я
,
для норм. зн-я
![]() =0
=0
Если >0, то крив-я теоретич распред-я будет более высокой и острой, чем норм расп-е с теми же параметрами.Если <0, то теоретич крив-я будет более низкой и плоской

Вопрос 27Нерав-во Маркова
Теорема: Если
![]() 0
и сущ-т М(х), то для любого >0
справедливо нер-во
0
и сущ-т М(х), то для любого >0
справедливо нер-во
![]()
Доказательство:
Т.к. события
иx<
противоположны и сумма их вер-тей равна
1, то из нер-ва(2) следует(1).Нер-ва (1) и (2)
служат для решения задач и т.д. Замечание:1)
нер-во(1) применяют если з-н распред-я не
известен, а известно лишь то, что
0
и М(х). 2) из (1) следует что F()![]()
![]() .
С ростом
оценка ф-ции и расп-я станов-ся достаточно
хорошей.
.
С ростом
оценка ф-ции и расп-я станов-ся достаточно
хорошей.
