Вопрос 10 Понятие дискретной случайной величины и ее з-на распределения. Многоугольник распределения.

СВ называется дискретной, если множество ее возможных значений конечно или счетно. Например, число бросаний монеты до появления герба или число выпавших очков при бросании игрального кубика.

Для полного задания СВ необходимо указать множество ее возможных значений и определить некоторое соответствие между отдельными ее значениями x_i (или некоторыми подмножествами) и вероятностями p_i, с которыми эти значения (или подмножества) принимаются. для СВДТ достаточно указать зависимость p_i = P{X = x_i} или таблицу.Так же ставят в соответствие вероятности не отдельные значения СВ, а множество значений (X < x), где x – произвольное число

Вопрос 11.Функцией распределения (ФР) (или интегральным законом распределения) СВ X называется числовая функция F(x) = P{X < x}, определенная для любых x  R. Свойства ФР:

1. 0  F(x)  1;

2. F(x₁)  F(x₂), если x₁  x₂, т.е. F(x) - неубывающая функция;

3. 

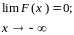
4. P{a  X  b} = F(a) - F(b).

Вопрос 12.Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа св х формулой:

m_X = M[X] =

Математическое ожидание существует, если ряд (соответственно интеграл) в правой части формулы сходится абсолютно. Если m_X = 0, то СВ Х называется центрированной (обозначается ).

Свойства математического ожидания:

1. M[C] = C, где С - константа;

2. M[CX] = CM[X];

3. M[X+Y] = M[X]+M[Y], для любых СВ X и Y;

4. M[XY] = M[X]M[Y] + K_XY, где K_XY = M[ ] - ковариация СВ X и Y.

Вопрос 13.Различают СВ дискретного типа (сокращенно СВДТ) и СВ непрерывного типа (сокращенно СВНТ). СВ называется СВДТ, если множество ее возможных значений конечно или счетно. Например, число бросаний монеты до появления герба или число выпавших очков при бросании игрального кубика. СВ называется СВНТ, если множество ее возможных значений заполняют интервал числовой оси. Например, время до отказа прибора (время “жизни” прибора) или погрешность измерения.

Для полного задания СВ необходимо указать множество ее возможных значений и определить некоторое соответствие между отдельными ее значениями x_i (или некоторыми подмножествами) и вероятностями p_i, с которыми эти значения (или подмножества) принимаются. Любое такое соответствие называется законом распределения СВ. Например, для СВДТ достаточно указать зависимость p_i = P{X = x_i} или таблицу следующего вида:

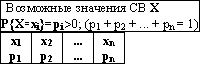
Для СВНТ такие способы не годятся, поэтому ставят в соответствие вероятности не отдельные значения СВ, а множество значений (X < x), где x - произвольное число. Этот способ годится для СВДТ и для СВНТ.

Вопрос14.Повторные независимые испытания. Ф-ла Бернулли.

ОПР: последовательность испытаний проводимых в неизменных условиях называется независимой относительно событию А если вероятность появления события А в любом испытании не зависит от исходов др испытаний.

Теорема: Пусть в n повторных независимых испытаниях известна вероятность Р(А) наступлений события А в каждом из испытаний тогда Р(А^-)=1-р=q, тогда вероятность того что событие А наступит равно к раз, независимо в какой последовательности, находится по ф-ле Pn(k)=Cn^kp^kq^n-k=(n!/k!(n-k)!) x p^kq^n-k – Формула Бернулли

Д-во: Рассмотрим событие В В=АА…А А^-А^-А^-

В силу независимости Р(В)=рр…рqq…q=p^kq^n-k 1, 2, 3…n (к-элементов)

Всего таких событий В с иными последовательностями наступления события А будет Cn^k значит по теореме сложения получается формула Бернулли