Спектр Излучения Атома Водорода

В нагретом до высокой температуры водороде можно наблюдать характерный линейчатый спектр. Все спектральные линии группируются в серии в зависимости от того, на какой энергетический уровень переходят электроны.

Переходы в первые возбужденные состояния на второй энергетический уровень с верхних уровней образуют серию Бальмера (n = 2), при переходе на первый энергетический уровень с n = 1 образуют серию Лаймана (рис. 113).

27 Модель Бора Представьте, что электроны в атоме движутся по определенным электронным орбитам - по аналогии с движениями планет Солнечной системы. Каждая планета движется по своей орбите, так и электроны вращаются вокруг ядра атома. Каждая такая орбита для электрона получила название "уровень энергии". Энергия электронов в атоме может изменяться только скачкообразно. Т.е. электрон может перескакивать с одной орбиты на другую и обратно (но не может занимать положение между орбитами). Говорят, что энергетические состояния электронов в атоме квантованы.  Энергия электрона зависит от радиуса его орбиты. Минимальная энергия у электрона, который находится на ближайшей к ядру орбите. 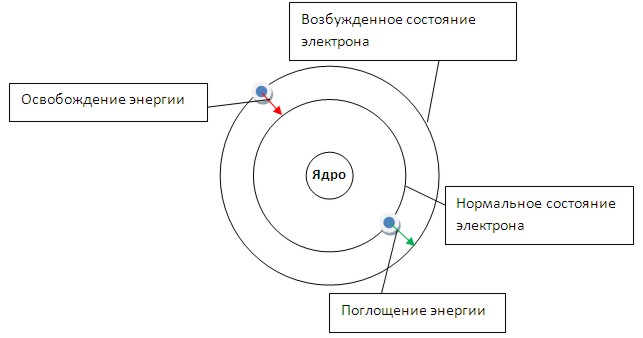При поглощении кванта энергии электрон переходит на орбиту с более высокой энергией (возбужденное состояние). И наоборот, при переходе с высокого энергетического уровня на более низкий - электрон отдает (излучает) квант энергии.    Кроме того, Бор указал, что разные энергетические уровни содержат разное количество электронов: первый уровень - до 2 электронов; второй уровень - до 8 электронов… 

28 Гипотеза де Бройля Луи де Бройль распространил представление о двойственной природе света на все микрочастицы материи - электроны, протоны, атомы и т. д. Еще в классической  физике ряд оптических явлений интерпретировался с точки зрения на свет как на волновой процесс (интерференция, дифракция). С другой стороны, некоторые явления с участием света могли быть  поняты только на основе представлений о свете как потоке частиц (корпускул) (фотоэффект, эффект Комптона и др.). Нетрудно установить соотношение между массой фотона m - частицы света и частотой электромагнитной волны света w, характеризующей его волновые свойства. В соответствии с известным соотношением Эйнштейна фотону с энергией ћw соответствует энергия mc²

 

                                                                                                    (1.5)

 

здесь с - скорость света.

Отсюда

                                                                                                       (1.6)

 

Учитывая, что импульс фотона p = mc, получим из (1.6)

 

                                                                                               (1.7)

 

Здесь учтено соотношение между частотой света w  и его длиной волны l:

w = 2pс/l.

29 Соотношение неопределенностей Гейзенбе рга

Попытаемся определить значение координаты х свободно летящей микрочастицы, поставив на ее пути щель шириной D х, расположенную перпендикулярно к направлению движения частицы.

До прохождения частицы через щель р_х имеет точное значение, равное 0, так что неопределенность импульса Dр_х=0, зато координата х частицы является совершенно неопределенной. В момент прохождениячастицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность D х, но это достигается ценой утраты определенности значения р_х. Действительно, вследствии дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах некоторого угла 2j , гдеj - угол, соответствующий первому дифракционному минимуму. Таким образом, появляется неопределенность импульса Dр_х=рsinj . (8)

Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной Dх соответствует угол j , для которого [ cм. (4.8) при b=Dх и m=1] sinj=l/ Dх. (9) Cледовательно Dр_х=рl/ Dх. (10) Отсюда с учетом (1) получается соотношение DхDр_х =рl=h (11) В общем случае соотношение

DхDр_х  h,DyDр_y  h, DzDр_z  h (12)

называют соотношением неопределенностей Гейзенберга. Из него следует, что чем точнее определена координата (Dх мало, т.е. узкая щель), тем больше неопределенность в импульсе частицы Dр_х  h/Dх. Точность определения импульса будет возрастать с увеличением ширины щели Dх [ cм. (9), (8)] и при Dх®¥ не будет наблюдаться дифракционная картина, и поэтому неопределенность импульса Dр_х будет такой же, как и до прохождения частицы через щель, т.е. Dр_х=0. Но в этом случае не определена координата х частицы, т.е. Dх®¥. Невозможность одновременно точно определить координату и импульс (скорость) не связана с несовершенством методов измерения или измерительных приборов. Соотношение неопределенности является квантовым ограничением применимости классической механики к микрообъектам.