
- •Статика Лекция 1. Основные понятия и аксиомы статики. Система сходящихся сил
- •1.1. Основные понятия статики
- •1.2. Аксиомы статики
- •1.3. Связи и их реакции
- •1.4. Система сходящихся сил
- •1.5. Условия равновесия системы сходящихся сил
- •1.6. Решение задач статики
- •Лекция 2. Теория пар
- •2.1. Момент силы относительно точки и оси
- •2.2. Пара сил и ее момент
- •2.3. Теоремы о парах
- •2.4. Условия равновесия системы пар сил
- •Вопросы для самоконтроля
- •Лекция 3. Основная теорема статики и условия равновесия пространственной системы сил
- •3.1. Лемма о параллельном переносе силы
- •3.2. Основная теорема статики
- •3.3. Приведение системы сил к двум силам
- •3.4. Условия равновесия пространственной системы сил
- •3.5. Теорема Вариньона
- •3.6. Условия равновесия плоской системы сил
- •Кинематика Лекция 4. Кинематика точки
- •4.1. Некоторые определения
- •4.2. Способы задания движения точки
- •4.3. Определение скорости точки
- •4.4. Определение ускорения точки
- •4.5. Частные случаи движения точки
- •Лекция 5. Простейшие движения твердого тела
- •5.1. Поступательное движение твердого тела
- •5.2. Вращение твердого тела вокруг неподвижной оси
- •5.3. Угловая скорость твердого тела
- •5.4. Угловое ускорение твердого тела
- •5.5. Частные случаи вращательного движения
- •5.6. Скорость и ускорение точки тела, вращающегося вокруг
- •Лекция 6. Сложное движение точки
- •6.1. Основные определения
- •6.2. Определение абсолютной скорости точки
- •6.3. Определение абсолютного ускорения точки
- •Лекция 7. Плоское движение твердого тела
3.6. Условия равновесия плоской системы сил
 Систему
сил, линии действия которых лежат в
одной плоскости, называют плоской. Пусть
эта плоскость совпадает с координатной
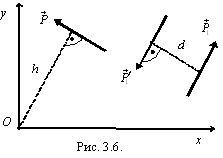
плоскостью Oxy (рис. 3.6).
Тогда векторы моментов сил относительно
любой точки плоскости и векторы моментов
пар сил перпендикулярны плоскости
действия сил и полностью определяются
своими алгебраическими значениями.
Систему
сил, линии действия которых лежат в
одной плоскости, называют плоской. Пусть
эта плоскость совпадает с координатной
плоскостью Oxy (рис. 3.6).
Тогда векторы моментов сил относительно
любой точки плоскости и векторы моментов
пар сил перпендикулярны плоскости
действия сил и полностью определяются
своими алгебраическими значениями.
Алгебраический момент силы относительно точки равен взятому с определенным знаком произведению модуля силы на ее плечо относительно точки
![]() .
(3.10)
.
(3.10)
Алгебраический момент пары сил равен взятому с определенным знаком произведению модуля одной из сил пары на ее плечо
![]() .
(3.11)
.
(3.11)
Знак «плюс» в формуле (3.10) берем в том случае, когда сила стремится повернуть тело вокруг точки О против часовой стрелки, знак «минус» соответствует повороту по часовой стрелке. Аналогично определяют и знак момента в формуле (3.11). Введенные таким образом алгебраические моменты совпадают с моментами сил и пар относительно осиOz, направленной к нам.
Условия равновесия плоской системы сил получим из уравнений (3.6). Так как все силы лежат в плоскости Oxy, их проекции на ось Oz и моменты относительной осей Ox иOy равны нулю, поэтому 3, 4 и 5-е уравнения выполняются тождественно. Оставшиеся уравнения, используя введенные алгебраические моменты, запишем так:
![]() .
(3.12)
.
(3.12)
Таким образом, для равновесия плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси и сумма алгебраических моментов всех сил относительно произвольной точки плоскости их действия равнялись нулю.
Пример 1. На раму AB (рис. 3.7,а) действуют сила F = 2 кН и пара сил, момент которой M = 1 кНм.
Определить реакции опор.
Рассмотрим
равновесие рамы AB,
которую освободим от связей, заменив
их действие реакциями (рис. 3.7,б): ![]() –
составляющие реакции неподвижного
цилиндрического шарнира A;
–
составляющие реакции неподвижного
цилиндрического шарнира A; ![]() –
реакция подвижного цилиндрического
шарнира B,
направленная перпендикулярно опорной
плоскости.
–
реакция подвижного цилиндрического
шарнира B,
направленная перпендикулярно опорной
плоскости.
Разложим
силы ![]() и
на
составляющие, параллельные координатным
осям:
и
на
составляющие, параллельные координатным
осям:
![]() кН;
кН; ![]() кН;
кН;
![]() .
.
Пара сил задана величиной момента и направлением действия.

Для полученной плоской системы сил запишем три уравнения равновесия:

При составлении уравнений равновесия целесообразно координатные оси направить перпендикулярно неизвестным силам, а моменты сил вычислять относительно точек пересечения линий действия неизвестных сил, что обеспечит получение наиболее простых уравнений, содержащих минимальное число неизвестных. Из уравнений равновесия получим
![]()
![]() кН;
кН;
![]() кН;
кН;
![]() .
.
Для проверки правильности решения рассмотрим условие равновесия, не использованное при решении примера. Выберем точку, относительно которой все найденные реакции имеют моменты (точка D, см. рис. 3.7,б), и вычислим сумму моментов всех действующих на раму сил относительно этой точки:
![]()
![]() .
.
Условие равновесия выполнено.
Ответ: ![]()
Отрицательные значения реакций показывают, что действительные направления сил и противоположны первоначально выбранным (см. рис. 3.7,б).
Пример 2. На консольную балку AB, показанную на рис. 3.8,а, действуют сила Р = 1 кН, пара сил, момент которой M = 3 кНм, и равномерно распределенная нагрузка интенсивностью q = 2 кН/м.
Определить реакцию жесткой заделки А.

В
этом примере используем не рассматривавшуюся
ранее связь, называемую жесткой
заделкой.
Она препятствует перемещению точки А и
повороту балки вокруг этой точки. На
закрепленный конец балки действует
распределенная система реактивных сил,
которую можно привести к силе, приложенной
в точке А,
и паре сил. Представим силу составляющими
,
,
а момент пары обозначим через ![]() .
.
Таким
образом, освобождая балку от связи,
покажем три составляющие реакции жесткой
заделки:
,
,
(рис.
3.8,б). Равномерно распределенную нагрузку
заменим ее равнодействующей, приложенной
в середине нагруженного участка, ![]() кН.
Итак, на балку действует плоская система
сил и пар сил. Запишем три уравнения
равновесия этой системы:
кН.
Итак, на балку действует плоская система
сил и пар сил. Запишем три уравнения
равновесия этой системы:

из которых получим
![]() = P =
1 кН;
= P =
1 кН; ![]() =
6 кН;
=
6 кН;
![]() =
21
+ 4,56 3
= 26 кНм.
=
21
+ 4,56 3
= 26 кНм.
Для проверки правильности решения вычислим сумму моментов всех сил, действующих на балку, относительно точки В
![]() .
.
Ответ: ![]() .
.
