1.5. Условия равновесия системы сходящихся сил
Так как система сходящихся сил имеет равнодействующую, для ее равновесия необходимо и достаточно, чтобы эта равнодействующая равнялась нулю:
.
(1.4)
Тогда силовой многоугольник (см. рис. 1.14) оказывается замкнутым, откуда следует геометрическое условие равновесия: «Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на силах системы, был замкнут».
При выполнении условия (1.4) из формулы (1.3) получим
,
откуда с учетом (1.2) следуют уравнения равновесия:
.
(1.5)
Таким образом, получены аналитические условия равновесия: «Для равновесия системы сходящихся сил необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из трех координатных осей равнялись нулю». В случае плоской сходящейся системы сил используют два из трех уравнений равновесия (1.5).
Теорема о трех силах. Если тело находится в равновесии под действием трех сил, и линии действия двух сил пересекаются, то все силы лежат в одной плоскости, а их линии действия пересекаются в одной точке.
Доказательство
Пусть линии действия сил и , приложенных в точках A и B, пересекаются в точке O (рис. 1.15).
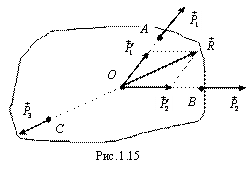
Перенесем
силы в эту точку и заменим их
равнодействующей
,
в результате чего получим уравновешенную
систему двух сил 
0,
откуда на основании аксиомы 1 следует,
что силы
и 
направлены
вдоль одной прямой. Таким образом, линии
действия всех сил пересекаются в точке O,
а сами силы лежат в одной плоскости.
Теорема доказана.
1.6. Решение задач статики
План решения задач статики следующий:
1) выбрать объект равновесия, т.е. тело (отдельную точку), равновесие которого (которой) будем рассматривать;
2) показать активные силы, действующие на объект равновесия;
3) освободить объект равновесия от связей и показать их реакции;
4) установить тип полученной системы сил и сформулировать условия равновесия;
5) определить из условий равновесия неизвестные величины.
Пример. Шар весом G подвешен на нити BC, составляющей с вертикалью угол , и опирается в точке A на гладкую вертикальную стену (рис. 1.16).
Определить реакции стены N и нити T.
Решение
Рассмотрим
равновесие шара. На него действуют: сила
тяжести 
–
активная сила, реакции стены 
и
нити 
(см.
рис. 1.16,а). Реакция гладкой стены
направлена
по нормали к стене и проходит через
центр шара O,
где приложена сила тяжести
.
Так как шар находится в равновесии под
действием трех сил, линия действия
силы
должна
проходить через точку пересечения линий
действия сил
и
,
т.е. через центр шара O.
Таким образом, на шар действует плоская
сходящаяся система сил.
Используем геометрическое условие равновесия – построим силовой треугольник (см. рис. 1.16,б), из которого получим
.
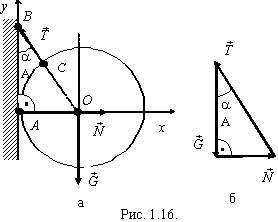
Решим эту задачу с помощью аналитических условий равновесия. Проведем координатные оси Ax и Ay и составим два уравнения равновесия:
из которых получим
.