- •Статика Лекция 1. Основные понятия и аксиомы статики. Система сходящихся сил
- •1.1. Основные понятия статики
- •1.2. Аксиомы статики
- •1.3. Связи и их реакции
- •1.4. Система сходящихся сил
- •1.5. Условия равновесия системы сходящихся сил
- •1.6. Решение задач статики
- •Лекция 2. Теория пар
- •2.1. Момент силы относительно точки и оси
- •2.2. Пара сил и ее момент
- •2.3. Теоремы о парах
- •2.4. Условия равновесия системы пар сил
- •Вопросы для самоконтроля
- •Лекция 3. Основная теорема статики и условия равновесия пространственной системы сил
- •3.1. Лемма о параллельном переносе силы
- •3.2. Основная теорема статики
- •3.3. Приведение системы сил к двум силам
- •3.4. Условия равновесия пространственной системы сил
- •3.5. Теорема Вариньона
- •3.6. Условия равновесия плоской системы сил
- •Кинематика Лекция 4. Кинематика точки
- •4.1. Некоторые определения
- •4.2. Способы задания движения точки
- •4.3. Определение скорости точки
- •4.4. Определение ускорения точки
- •4.5. Частные случаи движения точки
- •Лекция 5. Простейшие движения твердого тела
- •5.1. Поступательное движение твердого тела
- •5.2. Вращение твердого тела вокруг неподвижной оси
- •5.3. Угловая скорость твердого тела
- •5.4. Угловое ускорение твердого тела
- •5.5. Частные случаи вращательного движения
- •5.6. Скорость и ускорение точки тела, вращающегося вокруг
- •Лекция 6. Сложное движение точки
- •6.1. Основные определения
- •6.2. Определение абсолютной скорости точки
- •6.3. Определение абсолютного ускорения точки
- •Лекция 7. Плоское движение твердого тела
Статика Лекция 1. Основные понятия и аксиомы статики. Система сходящихся сил
1.1. Основные понятия статики
Статика – это раздел теоретической механики, в котором рассматривают операции преобразования систем сил в системы, им эквивалентные, и изучают условия равновесия материальных тел под действием сил.
Равновесие будем рассматривать по отношению к системе отсчета, жестко связанной с Землей. Тела, изучаемые в статике, будем считать абсолютно твердыми, т.е. такими, для которых расстояния между любыми двумя точками всегда остаются неизменными. В дальнейшем такие тела будем называть просто твердыми.
Сила –
это векторная величина, являющаяся
мерой механического действия одного
материального тела на другое. Она
характеризуется модулем, направлением
и точкой приложения. Точка приложения
силы и ее направление определяют линию
действия силы. На рис. 1.1 показана сила![]() ,
приложенная в точке A,
а NМ –
линия действия силы. Единицей измерения
силы в системе СИ является 1 Н. Совокупность
нескольких сил
,
приложенная в точке A,
а NМ –
линия действия силы. Единицей измерения
силы в системе СИ является 1 Н. Совокупность
нескольких сил ![]() ,
действующих на данное тело или систему
тел, называют системой
сил.
,
действующих на данное тело или систему
тел, называют системой
сил.
 Будем
называть свободным такое
твердое тело, на перемещения которого
не наложено никаких ограничений.
Будем
называть свободным такое
твердое тело, на перемещения которого
не наложено никаких ограничений.
Если
одну систему сил ![]() ,
действующих на свободное твердое тело,
можно заменить другой системой
,
действующих на свободное твердое тело,
можно заменить другой системой ![]() и
при этом состояние покоя или движения
тела не изменится, то такие системы сил
называют эквивалентными,
что обозначают так:
и
при этом состояние покоя или движения
тела не изменится, то такие системы сил
называют эквивалентными,
что обозначают так:
.
Если
система сил эквивалентна одной силе,
т.е.
![]() ,
то силу
называют равнодействующей данной
системы сил. Отметим, что не каждая
система сил имеет равнодействующую.
,
то силу
называют равнодействующей данной
системы сил. Отметим, что не каждая
система сил имеет равнодействующую.
Систему сил, под действием которой свободное твердое тело может находиться в состоянии покоя, называют уравновешенной или эквивалентной нулю: 0. Если система сил имеет равнодействующую, то силу, равную ей по модулю и действующую вдоль той же прямой в противоположном направлении, называютуравновешивающей.
1.2. Аксиомы статики
Аксиомы статики – это законы, установленные непосредственными наблюдениями и опытной проверкой следствий, логически вытекающих из аксиом.
Аксиома 1. Система двух сил, действующих на свободное твердое тело, является уравновешенной тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны.
На рис. 1.2 показаны две уравновешенные системы сил:
![]() 0;
0; ![]() 0.
0.

Аксиома 1 дает необходимые и достаточные условия уравновешенности системы двух сил, две следующие аксиомы устанавливают простейшие операции, приводящие к эквивалентным системам сил.
Аксиома 2. Если к данной системе сил добавить или отнять от нее уравновешенную систему сил, то полученная система сил будет эквивалентна исходной.
Из этой аксиомы вытекает следствие: «Действие силы на твердое тело не изменится, если перенести точку приложения силы вдоль линии ее действия».
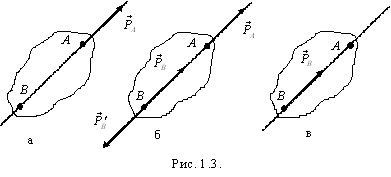
Для
доказательства следствия рассмотрим
силу ![]() ,
приложенную в точке A (рис.
1.3,а). В точке B на линии действия силы
приложим уравновешенную систему сил
,
приложенную в точке A (рис.
1.3,а). В точке B на линии действия силы
приложим уравновешенную систему сил ![]() ,
где
,
где ![]() .
Тогда в соответствии с аксиомой 2
получим
.
Тогда в соответствии с аксиомой 2
получим
![]() (рис.
1.3,б). Согласно аксиоме 1 система сил
(рис.
1.3,б). Согласно аксиоме 1 система сил ![]() 0,
а согласно аксиоме 2 их можно отбросить
(рис. 1.3,в),
т.е.
0,
а согласно аксиоме 2 их можно отбросить
(рис. 1.3,в),
т.е.
![]() ,
что и доказывает следствие.
,
что и доказывает следствие.
Таким образом, сила, приложенная к абсолютно твердому телу, является скользящим вектором.
Аксиома 3 (аксиома параллелограмма сил). Система двух сил, приложенных к телу в одной точке, имеет равнодействующую, приложенную в той же точке и равную геометрической сумме сил.
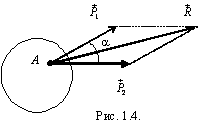
Эта
аксиома не только устанавливает
существование равнодействующей
рассматриваемой системы сил
![]() (рис.
1.4), но и дает правило ее определения:
(рис.
1.4), но и дает правило ее определения: ![]() .
Модуль равнодействующей
.
Модуль равнодействующей
![]() .
.
Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
Силы взаимодействия двух тел удовлетворяют всем условиям аксиомы 1, кроме одного – они приложены к разным телам (рис. 1.5), и поэтому не образуют уравновешенную систему сил.
|
|
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела не нарушится, если тело станет абсолютно твердым.
Другими словами, при равновесии деформируемого тела силы, действующие на него, удовлетворяют тем же условиям, что и для абсолютно твердого тела, но эти условия для деформируемого тела будут только необходимыми, не являясь достаточными.
Рассмотрим
в качестве примера деформируемого тела
нить, которая находится в равновесии
под действием двух сил ![]() и
и ![]() ,
приложенных к ее концам, как показано
на рис. 1.6,а. В соответствии с аксиомой
1 эти силы должны действовать вдоль
одной прямой (вдоль нити) в противоположные
стороны и иметь одинаковые модули. Для
того, чтобы эти условия стали достаточными,
к ним следует добавить еще одно: силы,
действующие на нить, должны быть
растягивающими. При тех же условиях
абсолютно твердое тело – стержень (рис.
1.6,б) будет находиться в равновесии под
действием как растягивающих, так и
сжимающих сил.
,
приложенных к ее концам, как показано
на рис. 1.6,а. В соответствии с аксиомой
1 эти силы должны действовать вдоль
одной прямой (вдоль нити) в противоположные
стороны и иметь одинаковые модули. Для
того, чтобы эти условия стали достаточными,
к ним следует добавить еще одно: силы,
действующие на нить, должны быть
растягивающими. При тех же условиях
абсолютно твердое тело – стержень (рис.
1.6,б) будет находиться в равновесии под
действием как растягивающих, так и
сжимающих сил.