- •Закон распределения случайных процессов (зр сп)
- •1. Исходные понятия и определения.
- •Функция распределения случайного процесса
- •Плотность вероятностей случайного процесса.
- •Характеристическая функция случайного процесса
- •Моментные функции случайных процессов
- •Одномерные моментные функции сп.
- •Корреляционная функция сп
- •Взаимная корреляционная функция сп
- •Моментные функции конструктивных сп.
- •Основные классы сп
- •Стационарные случайные процессы
- •Периодические случайные процессы.
- •Случайные процессы второго порядка (Марковские процессы)
- •Аналитические свойства случайных процессов (сп)
- •1 Простейшие преобразования сп
- •Корреляционный анализ линейных систем (лс)
- •Нелинейные преобразования сп
- •Сп с дискретным спектром
- •Сп с непрерывными спектрами
- •Сп с независимыми приращениями (нп)
- •Белый шум (бш)
- •Модели флуктуационных процессов
- •Точечное оценивание вероятностных характеристик случайных величин.
- •Экспериментальное получение характеристик случайного процесса.
Аналитические свойства случайных процессов (сп)
1. Простейшие преобразования СП
2. Непрерывность СП
3. Дифференцирование СП
4. Интегрирование СП
1 Простейшие преобразования сп
1.1 ![]() ,
,
где
![]() ,
,![]() – детерменированние функции;
– детерменированние функции;
![]() – СП.
– СП.
Все последующие задачи будем рассматривать в рамках корреляционной теории.
Найдем математическое
ожидание (МО) процесса
![]()
![]()
![]()
Найдем
![]()
![]()
Таким образом
![]()
Возникает вопрос может ли быть процесс стационарным случайным процессом (ССП)?
1) МО в общем случае не
равно const.
В частности, когда
,
![]() – const,
тогда
– const,
тогда
![]() – const.
– const.
Возможно, что
– const
при
– const
и
![]() – const.
– const.
2) В общем случае данный процесс является нестационарным
1.2.
![]() (линейная комбинация СП)
(линейная комбинация СП)
1.
![]()
2.

Частный случай, если
все
![]() и входящие в сумму процессы некоррелированы
корреляционная функция суммы равна
сумме корреляционных функций
и входящие в сумму процессы некоррелированы
корреляционная функция суммы равна
сумме корреляционных функций
Процесс такого вида
является нестационарным, однако при
![]() и процессы
и процессы
![]() – стационарно связанные.
– стационарно связанные.
3. Пусть все – некоррелированы
![]() .
.
Если сумма бесконечна
имеет ли смысл рассматривать процесс
?
Когда
![]() необходимо потребовать, чтобы
необходимо потребовать, чтобы
![]() (Так как в рамках корреляционной теории
дисперсия должна быть конечной).
(Так как в рамках корреляционной теории
дисперсия должна быть конечной).
![]() ,
разложения СП
,
разложения СП
Каноническое разложение СП (один из видов)
![]() (другой вариант), где
(другой вариант), где
![]() – детерминированная функция,
– детерминированная функция,
![]() – случайная величина (СВ).
– случайная величина (СВ).
Эти канонические разложения ввел академик Пугачев (в его книге описано получения этих канонических разложений).
Функции и называются координатными функциями в канонических разложениях.
1.3. ![]() ,
,
![]()
![]()
![]()
Модуль возникает из-за
физического смысла
![]()

Если действительная и
мнимая часть некоррелированы, то
![]() – действительная функция. Таким образом
если
– действительная, то это не значит, что
сам процесс действителен. Процесс будет
стационарен, если Re
и Im
являются стационарно свзанными.
Комплексный СП
называется гильбертовым если он обладает
конечной дисперсией, то есть
– действительная функция. Таким образом
если
– действительная, то это не значит, что
сам процесс действителен. Процесс будет
стационарен, если Re
и Im
являются стационарно свзанными.
Комплексный СП
называется гильбертовым если он обладает
конечной дисперсией, то есть
![]() (Аналогия с ТПС, конечная средняя
мощность или процессы с конечной
энергией).
(Аналогия с ТПС, конечная средняя
мощность или процессы с конечной
энергией).
Дисперсия характеризует не только размах значений, с точки зрения энергии она характеризует среднюю мощность СП.
2
Функция
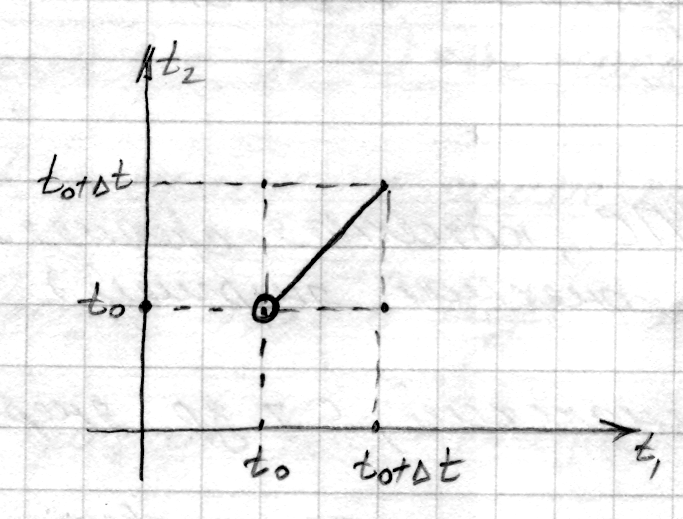
![]() непрерывна в точке
непрерывна в точке
![]() ,
когда
,
когда
![]()
Последовательность
![]() если
если
Для СВ существует 4 вида сходимости
с вероятностью 1
по вероятности
среднеквадратическая
по распределению
Распишем среднеквадратическую метрику
![]()
Возникает необходимость в решении предела, что является проблематично. Как уйти от предела? Лоэв решил эту проблему, предложив критерий, названый в его честь.
![]() тогда
тогда
![]()
Определение СП
называется непрерывным при
![]() если
если
![]() (1.1)
(1.1)
Целью является определение
свойств МО,
![]() через существование (1.1)
через существование (1.1)
![]()
Если
![]() то
то
![]() в этой точке
в этой точке
![]() – непрерывной и по диагонали
– непрерывной и по диагонали
|
если
Этот процесс стохастически непрерывным
1)
– непрерывна на
диагонали, то есть при
|
Таким образом для
непрерывности СП необходимо, чтобы
непрерывна была
![]() и
.
и
.
1.2)
– ССП (условие непрерывности для
![]() не нужно, так как
не нужно, так как
![]() )
)
только
![]() при
при
![]() определяет непрерывность СП
определяет непрерывность СП
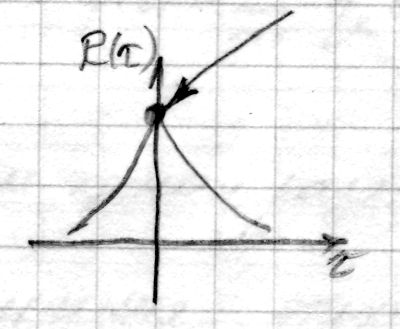
1.3) Из того, что является непрерывным не следует что его реализации являются непрерывными функциями.
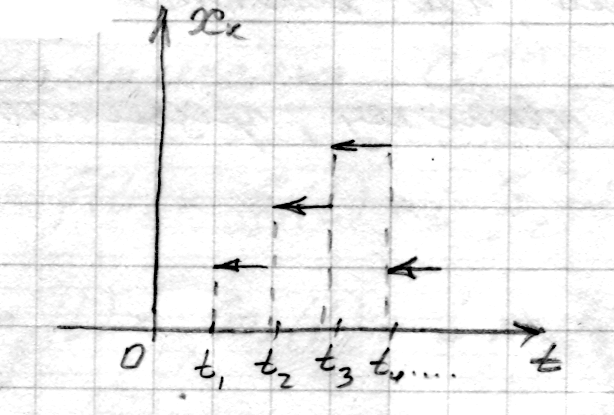
Пусть все реализации СП кусочно-постоянные, то есть имеют разрыв второго рода.
Такой процесс является
непрерывным если точки
![]() не являются фиксированными.
не являются фиксированными.
Если – не фиксированные, то точки случайным образом расположены на временной оси.
Пример

Процесс не является непрерывным так как его реализации имеют разрыв (всегда) в момент времени .
У случайного процесса доминирующими являются не реализации, а его вероятностные свойства.
3
Определение: Пусть
– непрерывный СП, тогда СП
![]() называется производной процесса
называется производной процесса
![]()
Воспользуемся критерием Лоэва для объяснения условий, которым должна удовлетворять и МО.

Вычислим предел вида

Для того, чтобы СП
![]() был дифференцирован в точке
необходимо и достаточно чтобы в этой
точке была дифференцируемая его
ковариационная функция.
был дифференцирован в точке
необходимо и достаточно чтобы в этой
точке была дифференцируемая его
ковариационная функция.
1. Если
дифференцируемая в любой точке
![]() ,
то процесс дифференцируемый на всей
временной оси.
,
то процесс дифференцируемый на всей
временной оси.
Вычислим условие которое должна удовлетворять и МО дифференцируемого СП.
2 .
Следовательно
.
Следовательно
![]() и
и
![]() должна существовать.
должна существовать.
3. – ССП.
![]()
![]()
![]()
4. Если СП является дифференцируемым, то это не значит, что дифференцируемыми являются его реализации.
4
Пусть – комплексный СП.
![]() ,
где
,
где
![]() – комплекснозначная функция.
– комплекснозначная функция.
Необходимо узнать условия которым должны удовлетворять характеристики СП , чтобы этот интеграл существовал или имел смысл.
Разбив промежуток
времени
![]() на точки
на точки![]()
![]() ,
,
![]()
Если предел при
![]()
![]() то тогда мы говорим, что существует
интеграл от СП.
то тогда мы говорим, что существует
интеграл от СП.

Согласно критерию Лоэва:


Если при
![]() предел существует, то СП
– интегрируем. Мы рассмотрим интеграл
вида
предел существует, то СП
– интегрируем. Мы рассмотрим интеграл
вида
![]() ,
однако часто необходимо рассматривать
,
однако часто необходимо рассматривать
![]()
Условие существования такого интеграла
![]()
Если
![]() – ССП все тоже самое, только
– ССП все тоже самое, только
![]()
Если весовая функция является спадающей, то ее наличие упрощает требования к ковариационной функции .