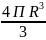36 Метод крамера.
Теорема: пусть
∆ - определитель матрицы системы, а ∆j
– опред-ль матрицы, полученной из
матрицы системы с заменой j-го
столбца столбцом своб.членов. Если ∆
,
то неизвестные
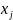находятся по формулам
=
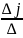(j=1,2,…,n)
Это формулы Крамера.
2 + - =8
- +2 = -1
-2 +3 =1
=
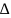2 1 -1
1 -1 2 = 5
4 -2 3
Сначала заменяем первый столбик.
1= 8 1 -1 = -24-2+2-1+32+3=10
-1 -1 2
1 -2 3
2= 2 8 -1 = -6+64-1-4-24-4=25
1 -1 2
4 1 3
3= -2-16-4+32-1-4= 5
=10/5=2
=25/5= 5
= 1.
№37. Метод Гаусса.
2 + - =8
- +2 = -1
-2 +3 =1
А= 2 1 -1
1 -1 2
4 -2 3
При решении этим методом расширенную матрицу системы с помощью элементарных преобразований приводят к ступенчатому виду, затем от нее возвращаются к системе и, начиная с последн. ур-ия, находят все неизвестные.
2
1 -1 8 1 -1 2 -1 1 -1 2 -1
1 -1 2 -1
0 3 -5 10
0 3 -5 10
4 -2 3 1 0 2 -5 5 0 0 -5 -5
-
+2
=
-1
3 -5 =10
-5 = -5
= -1+5-2*1= 2
=(10+5*1)* 1/3=5
=1
.
Производная сложной ф-ии
Пусть имеется функция Z=f(x,y). Причем (x,y) сами явл.функцией аргумента t.
X=u(t) ; y=u(t) тогда производная ф-ции Z находится по формуле :
=
*
+
*
.
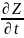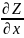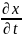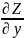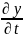Пусть Z=f(x,y), причем (x,y) сами явл-ся функциями двух переменных. X=u(t,g); y= v(t,g). Тогда частные производные ф-ии z по переменной (t,g) наход-ся по формулам:
= * + *
=
*
+
*
.
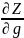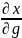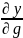№38. Система линейных однородных уравнений. Фундаментальная система решений.
Система из m линейных уравнения с n неизвестными, у которой все своб.члены = 0 назыв.системой лин.однор.уравнений.
+…+ =
+ +…+ = (*)
…………………………………………
+ +…+ =
Такие системы
всегда совместны, т.к.они имеют нулевое
решение.
=0,
,
=0.
Если кол-во ур-ий
системы (*) совпадает с кол-вом переменных,
то система имеет только нулевой решение
если при этом определитель системы
.
Действительно в этом случае все
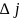из формул Крамера будут =0, как
определители,имеющие нулевой столбец.
Тогда
=0.
= =0
Т.о. ненулевые решения модут возникнуть в тех случаях, когда либо определитель системы =0, либо число ур-ий не совпадает с числом неизвестных.
ИЛИ: система (*) имеет ненулевые решения, если ранг этой системы меньше числа неизвестных, т.е r<n.
(r- строки, n- столбцы).
Свойства решения такой системы:
Обозначим решение
системы
=
,
=
,
=
.
=(
,
… ,
)
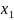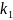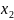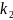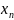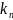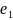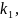Если строка =( , … , ) явл.решением системы(*), то строка λе также явл.решением системы (*)
Λе=(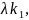
,
… ,
).
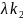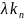λ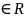
Если =( , … , ) и
=(
,
… ,
)
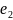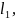
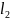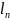явл.решением сист.(*), то их линейная
комбинация
+
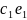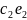также явл.решением этой системы.
+
=
(
+
,
+
,
… ,
+
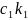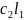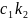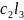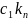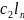
Интерес представляют линейно независимые решения системы через которые линейно выражаются все остальные решения.
Определение:
система линейно независимых решений
,
… ,
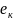называется фундаментальной если каждое
решение системы явл.линейной комбинацией
решений
,
… ,
.
Теорема: если ранг матрицы системы (*) меньше числа переменных, то всякая фундамент.система решений данной системы слстоит из n-r решений.
№22. Частные производные высших порядков
Частные производные ф-ции двух переменных сами явл.функциями двух переменных, Поэтому имеет смысл говорить о нахождении производных от этих производных.
Частной производной 2го порядка для функции Z=f(x,y) называется частная производная от ее частных производных. Аналогично определ.производные более высоких порядков.
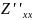– чистая частная
произв.2го порядка;
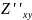- смешанная.
Доказано, что
=
.
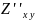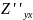Равенство выполняется для любых функциё
двух переменных. И при вычислениипроизводных
> высоких порядков результат
дифференцирования не зависит от порядка
дифференцирования. Например,
=
,
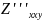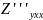но
≠
.
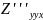№20. Ф-ии многих
переменных.Частные произв. Функцией
двух переменных назыв-ся такое правило,
при котором каждой паре значений
переменных ставится в соответствие
определенное значение третьей. Z=f(x,y)
X,y
– независимые переменные (аргументы);
Z-
зависимая переменная(функция).Область
определения 2х перем. – множество таких
пар (х,у) для которых соотв.значение Z
определено. Частные
производные. Пусть
имеется ф-ция
Z=f(x,y).
Так как Х и Y-
независимые переменные,то одна из них
может изменяться,а другая сохранять
свое значение. Дадим независ.переменной
Х приращение ∆х, сохраняя значение Y
неизменным. Тогда z
получит приращение,которое называется
частным приращением z
по Х и обозначается
.
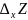Итак,
=f
(
+∆х; y)
– f(
;
).
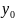Аналогично можно определить приращение
по у.
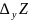=f
(
;
+∆у) – f(
;
).
Если существует конечный предел
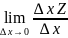, то он называется частной производной
функции Z
по переменной х. Аналогично для у.
Обозначение:
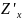или
.
Для нахождения частных производных
используем те же самые правила
дифференцирования что и для обычной
производной 1 переменной.Для нахождения
частной производной ф-ции по переменной
Х временно считают Y
постоянной величиной.
№24. Дифф.ур-ия
1пор-ка. Общ и част решен. Раздел.переменные
Дифф.уравнения
1 порядка – это уравнение вида
F(x,y,y’)=0.
Здесь х – независ.переменная; у –
неизв.ф-ция аргумента х; у’ –
производ.ф-ии у.
В записи
дифф.ур-ия могут отсутствовать в явном
виде х и у, однако произв.у’ обязана
присутствовать всегда. Решением
дифф.ур-ия 1 порядка назыв.такая ф-ция
у, которая при подстановке ур-ия обращает
его в верное равенство. Y
lny
+xy’=0.
Одним из решений явл.ф-ция у=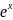
.
ln
+x
(
)’=
*x*1-ex*
=0.
Каждое из
решений назыв.частным решением. Совок-ть
всех частн.решений ур-ия представляет
собой общие решения дифф.ур-ия. Общее
решение записывается в виде y
=
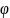(x,c).
Если найденную ф-ция невозможно разрешить
относительно у, то вид общ.решения:
(х,у,с)=0. (неявный вид) Уравнения
с разделяющимися переменными – это
уравнения,которые можно привести к
виду Р(х)*Q(у)dx+M(x)*N(y)dy=0
Р(х) и M(x)
- ф-ия аргумента х. Q(у)
и N(y)
- ф-ия аргумента у. При решении такого
уравнения стараются отделить переменные
х и у друг от друга разложив их по разным
частям.
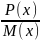dx
= -
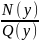dy.
Далее интегрируем
=
.
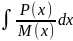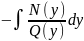В результате получаем общ.решение
ур-ия. Разносим х и у в разные стороны.
В некоторых задачах требуется найти
частное решение,удовл.начальному
условию у(
)=
.
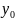В этом случае в общ.решение вместо х
подставляем
,а
вместо у -
.
Полученное ур-ие решают относит-но С.
Найденное значение С подставляют в
общ.решение.
№26. Дифф.ур-ия 2
порядка. Общее и частное решение.
Понижение порядка Ур-ия
вида F(x,y,y’,y’’)=0.
Где х – независ.перем.; у – неизв.ф-ция
аргумента х;
Y’,y’’
– 1 и 2 ее производная.Решением такого
ур-ия явл.ф-ция у(х),которая при подстановке
в уравнение обращает его в верное
равенство. Совок-ть всех решений
назыв.общим решением. Оно записано в
виде у= f(x,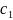
,
)
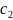или
(x,
y,
,
)=0.
Для поиска частного
решения ур-ия 2го порядка,
котор.удовлетв.начальному условию
у(
)=
поступают так: у’(
)=
.
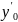В общ.решение у= f(x,
,
)
и в соотв.производную у’= f’(x,
,
)
подставляют
,
,
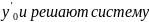
= f( , , )
= f’( , , ) относительно постоянных , . Найденные постоянные подставляют в общ.решение.
Ур-ия, допускающие понижение порядка Ур-ия не содержащие в явном виде y, y’, т.е.ур-ия вида F(y’)=0. Такие ур-ия можно привести к виду у’’=f(x). Для решения достаточно дважды проинтегрировать ф-ию f(x).
№19. Разложение в ряд элемент.функций.Ряд Тейлора - это степенной ряд вида
F(
)+
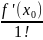(x -
)+
+…
=
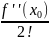
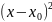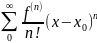Ряд Маклорена – то же самое,только
.
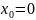Если такие ряды будут сходящимися, то
можно говорить о представлении ф-ции
f(x)
в виде таких степенных рядов. Для этого
должны выполняться след.условия: у
ф-ции f(x)
должны существовать производные любого
порядка в области сходимости ряда и
все эти производные по абсолютной
величине должны быть ограничены одним
и тем же числом.
Пример разложения в ряд маклорена: f(x)=
=1+x+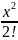
+
… =
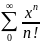Область сход-ти (-
)
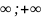№1. Понятие производной Пусть ф-ция у= f(x) определена на некотором промежутке. Рассмотрим точку этого промежутка и дадим ей произвольное по знаку достаточно малое приращение х. Приращение аргумента х очевидно вызовет и приращение функции у= f(x)- f( ).
Х= + х.
О п р е д е ле н и е: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется конечный предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Y ’=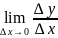
F’(
)=
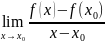
Таблица:
=kx^k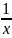-1;
(
)’=
-1/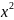
;
=
;
=
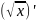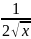ln
a; Ln x=1/x ;
=
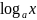1/ xln a;
Sin=cos;
cos=-sin; tg=1/
;
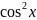ctg=
-1 /
;
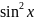arcsin=1/
;
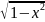arccos=
-1 /
;
arctg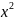= 1 /
+1
arcctg= -1 / +1
Правила:
(С*u)’=c*(u)’
(U±V)’=U’±V’
(U*V)’=U’V+UV’
(
)’=
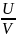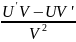
(f (φ(x) )’= f’(φ(x))* φ’(x)
№5. Определенный интеграл.Пусть дана непрерывная и неотрицат.ф-ция у= f(x) на отрезке [а,b]. Разобьем отрезок [а,b] на части точками , , … , , так что =a.
А=
<
< … <
<
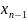=b
Получим
n
частичных отрезков. Длина каждого из
них
=
-
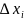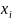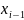
i-1, …, n.
На
каждом таком отрезке произвольно
выберем промежуточную точку
.
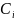Найдем значение ф-ции F
в каждой их этих точек F(
)
и составим произведения F(
)*
∆
.
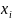Геометрически каждое такое произведение представляет собой площадь прямоугольника с основанием ∆ и высотой F( ). Рассмотрим сумму всех таких произведений.
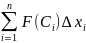
Ее принято называть интегральной суммой; геометрически она представляет собой ступенчатую фигуру,составленную из прямоуг-ков. S этой фигуры прилизит.равна S криволинейной трапеции, ограниченной сверху ф-цией f(x), снизу- осью ОХ, слева и справа прямыми х=а, х=в.
Приближенное равенство будет тем точнее,чем больше n. Точное равенство получится в пределе при n→+∞.
Если сущ-ет конечный предел интегральных сумм при n→+∞ , то он наз-ся опред.интегралом для ф-ции у= f(x) по отрезку [а,b].
Обозначение:
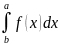
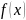– подынтегральная
ф-ция
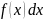– подынтегральное
выражение
А,в – верхн,нижн.границы
Из определения следует равенство
=
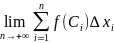
Таким образом S криволин.трапеции =
№7.
Геометрич.приложения опред.интеграла.
Вычисление
S
плоской фигуры:
S
криволин.трапеции =
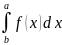
Если
ф-ия
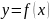лежит под осью Х (
),
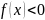то площадь фигуры = -
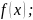У=
У=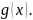
( две функции над осью х)
S=
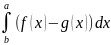
Объем
тела вращения: 1)V
тела,полученного в рез-те вращения
вокруг оси ох кривол.трапеции,
огранич.сверху ф-цией у=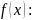
V=П
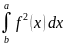2). V
шара радиуса R
V=
