
2.Первообр.
и неопред. интеграл.
Пусть имеется ф-ция у=f(x)
определенная на некотором промежутке.
Если существует ф-ция F(x)
такая,что в каждой точке этого промежутка
выполн-ся равенство F’(x)=
f(x)
,то ее называют первообразной. Любые 2
первообразные одной и той же ф-ции
отличаются друг от друга разве лишь на
постоянные слагаемые. Определение:
пусть имеется ф-ция f(x).
Неопред.интегралом этой ф-ции назыв-ся
всё множество её первообразной.
Обозначения:
 .f(x)
– подынтегральная ф-ция; f(x)dx
– подынтегральное выражение. Х –
переменная интегрирования. Из отпределения
следует
=
F(x)+C,
где F’(x)=
f(x).
С=const.
.f(x)
– подынтегральная ф-ция; f(x)dx
– подынтегральное выражение. Х –
переменная интегрирования. Из отпределения
следует
=
F(x)+C,
где F’(x)=
f(x).
С=const.
3.Св-ва неопред.интеграла.
1.
постоянный множитель можно выносить
за знак интеграла
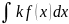 =
k
=
k
2. Интеграл от суммы функции = сумме интегралов от этих функций.
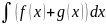 =
+
=
+
 .
.
3.
 = F(x)+C,
в частности
= F(x)+C,
в частности
 =
x
+ C.
=
x
+ C.
4.
 =
=

Таблица :
 =
=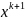 /k+1
/k+1
 =
ln|x|+C
=
ln|x|+C
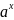 =
/lna+C;
=
/lna+C;
Sinx= - cosx; cos=sinx;
 =tgx;
=tgx;
 =
-ctgx;
=
-ctgx;
 =arcsin
=arcsin ;
;
 =arcsin
=arcsin
 =
=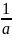 arctg
;
arctg
;
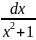 =
arctgx
;
=
arctgx
;
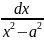 =
=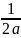 ln
ln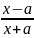 +c
+c
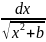 =
ln|
x+
=
ln|
x+ |
;
|
;
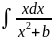 =
=
 ln │
ln │ │
│
4.Осн.Методы интегрир.
Два основных метода:
1. метод интегрирования по частям
Формула:
 =
UV
–
=
UV
–
 ,
,
Где U=U(x); V=V(x); dU=U’(x)dx; dV=V’(x)dx.
Пусть требуется вычислить некоторый неопред.интеграл. в этом интеграле выбирают часть,которую обозначают буквой U. тогда все оставшееся обозначится через dV. Далее, зная U с помощью производной находят dU, зная dV с помощью интегрирования находят V. Всё подставляют в правую часть формулы. Вновь полученный интеграл должен быть проще исходного.
Пример:
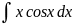 = │U=x;
dU=dx;
dV=cosxdx;
V=sinx│=
xsinx
-
= │U=x;
dU=dx;
dV=cosxdx;
V=sinx│=
xsinx
-
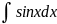 =
xsinx
+cosx+C.
=
xsinx
+cosx+C.
2. метод замены переменной.
=
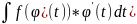
X=φ(t).
Пример:
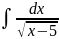 = │t=
= │t= ;
;
 x=
x= dx=2t
dt│=
dx=2t
dt│=
 =
2
=
2 = 2t+C
= 2
+C.
= 2t+C
= 2
+C.
8.Ряды.Необходимый признак
Рассм.бесконечную
последовательность действительных
чисел
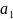 ,
,
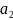 ,…,
,…,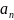 .
.
Числовой ряд-это
сумма всех этих членов. Обозначение
ряда:
 .
.
Рассмотрим частичные
суммы ряда:
 =
= ;
;
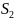 =
= ;
;
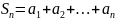 .
.
Рассм.последовательность
частичных сумм
 .
Если существует конечный предел при
n→∞
lim
.
Если существует конечный предел при
n→∞
lim =S,
то говорят, что соответствующий числовой
ряд сходится к этому числу S
и пишут
=S,
то говорят, что соответствующий числовой
ряд сходится к этому числу S
и пишут
 ,
в противном случае ряд называют
расходящимся.
,
в противном случае ряд называют
расходящимся.
11.Свойства сход-ся рядов.
Пусть
имеется числовой ряд
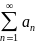 .
Отбросим k
первых членов этого ряда, оставшийся
ряд носит название k-ого
остатка исходного ряда
.
Отбросим k
первых членов этого ряда, оставшийся
ряд носит название k-ого
остатка исходного ряда

 - остаток.
- остаток.
 – k-тый
остаток.
– k-тый
остаток.
1.числовой ряд и любой его остаток сходятся или расходятся одновременно. Из этого свойства следует, что при исследовании ряда на сходимость можно игнорировать любое колич-во первых членов ряда.
2.Необходимое условие сходимости: Если числовой ряд сходится,то предел его общего члена равен нулю.
-
сходится =>
 =0.
=0.
Если
предел n-ого
члена числового ряда
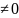 , то ряд расход. (
≠0,
то
- расх. ).
, то ряд расход. (
≠0,
то
- расх. ).
3.
пусть ряд с общим членом
сход-ся к S,
а С=const.
тогда ряд с общим членом
 также сход-ся причем к числу СS.
Таким образом умножение каждого члена
ряда на одно и то же число не меняет его
сходимости.
также сход-ся причем к числу СS.
Таким образом умножение каждого члена
ряда на одно и то же число не меняет его
сходимости.
4.
Если ряд с общим членом
сход-ся к сумме
, то ряд с общ.членом
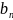 сход-ся к
,
то ряд с общ.членом
+
тоже явл-ся суммой
+
.
сход-ся к
,
то ряд с общ.членом
+
тоже явл-ся суммой
+
.
 =
+
.
=
+
.
№12. Признак сравнения.
Пусть
имеюся 2 положительных ряда
 и
и
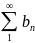 и пусть при любом n
выполняется неравенство
≤
,
тогда
1). Если
-сход.,то
-сход.
и пусть при любом n
выполняется неравенство
≤
,
тогда
1). Если
-сход.,то
-сход.
2). Если -расх., то -расх.
№13. Признак Даламбера
Пусть
имеется положит.числовой ряд
и пусть существует конечный предел
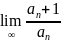 =Д,
тогда:
1)если Д>1, то ряд расх.
=Д,
тогда:
1)если Д>1, то ряд расх.
2). Если Д<1, то ряд сход.
3). Если Д=1, то признак не работает.
Признак
Коши:
Пусть
имеется положит.числовой ряд
и пусть существует конечный предел
 =k,
тогда 1. Если k>1
– ряд расх.
=k,
тогда 1. Если k>1
– ряд расх.
2. Если k<1- сход.
3. Если k=1 – признак не работает.
№14. Интегральный признак.
Пусть имеется положит.числовой ряд и пусть существует непрерывная убывающая ф-ция f(x) определенная на промежутке [1; +∞) такая, что f(n)= , тогда числ.ряд и сход.или расх-ся одновременно.
 .
С помощью интегр.признака можно доказать,
что при β≤1 ряд расх., а при β>1 ряд
сход-ся.
.
С помощью интегр.признака можно доказать,
что при β≤1 ряд расх., а при β>1 ряд
сход-ся.
Практически все числовые ряды с постоянными членами явл-ся расход-ся, исключение составляет ряд,состоящий из нулей - он сход-ся.
№15. Знакочередующиеся. Т.Лейбница.
Знакочередующимся называется числ.ряд, любые два соседних члена которого имеют разные знаки.
- +
+ -…=
-…=
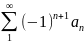
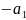 +
-
+…=
+
-
+…=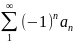
Т.Лейбница. Пусть имеется знакочередующийся ряд где n>0 и пусть при этом выполняется 2 условия:
Числ.последовательность с общ.членом
 убывает
убывает=0
Из этих двух следует, что исходный знакочеред.ряд сходится.
№16. Абсол.и усл.сход-ть ряда.
Рассм.ряд с
произвольными членами
(1) и соответствующий ему ряд из модулей
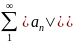 (2). Пусть ряд (1) сход.,тогда если при
этом ряд (2) тоже сход, то говорят, что
ряд (1) абсолютно сход-ся, а если же ряд
(2) при этом расх-ся, то говорят, что ряд
(1)условно сход-ся.
(2). Пусть ряд (1) сход.,тогда если при
этом ряд (2) тоже сход, то говорят, что
ряд (1) абсолютно сход-ся, а если же ряд
(2) при этом расх-ся, то говорят, что ряд
(1)условно сход-ся.
Достаточный признак абсол.сходимости. Пусть имеется произвольный числ.ряд. Если соответствующий ему ряд из модулей сход-ся, то исходный произв.ряд абсолютно сход-ся.
№17. Функциональные ряды. Область сходимости.
Функциональный ряд – ряд, членами которого явл-ся функции.
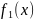 +
+ +…+
+…+
 +…=
+…=

Если в функц.ряд
вместо x
подставить какое-либо значение
 из области определения всех функций,
то функц.ряд превратится в числовой.
Полученный числовой ряд может как
сходиться,так и расходиться. Совокупность
всех значений переменной Х, при которых
функц.ряд сход-ся называется областью
сходимости функционального ряда.
из области определения всех функций,
то функц.ряд превратится в числовой.
Полученный числовой ряд может как
сходиться,так и расходиться. Совокупность
всех значений переменной Х, при которых
функц.ряд сход-ся называется областью
сходимости функционального ряда.
№18.Степенные ряды.
Степенной ряд – функц.ряд, члены которого представляют собой степенные функции.
 +
+ +
+ +
+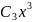 +… +
+… +
 …=
…=
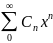
Здесь
,
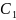 ,
,
 - действит.числа,называемые коэффициентами
степенного ряда.
- действит.числа,называемые коэффициентами
степенного ряда.
Все степ.ряды сход-ся в точке х=0, т.к.в этом случае все члены ряда кроме может быть первого =0. Существуют степ.ряды, которые сход-ся только при х=0. Такие ряды относятся к рядам 1го класса. При всех х отличных от нуля Д=∞ => при х ≠0 наш ряд расх-ся.
Сущ-ют
степ.ряды,котор.сход-ся при всех
действит.значениях х. Их отнесем к
рядам 2го класса. Все остальные ряды
отнесем к рядам 3го класса. Для всех
рядов 3 класса сущ-ет положит.число,называемое
радиусом сходимости (R),
такое что при х (-R;R)
ряд абсолютно сходится.
(-R;R)
ряд абсолютно сходится.
(-R;R) – интервал сходимости.
Чтобы найти область сходимости ряда 3го класса необходимо проверить сходится ли этот ряд на концах интервала, т.е.при х=- R и х= R. В зависимости от рез-тов проверки к интервалу сходимости либо не присоединяются концы, либо присоединяются один или оба.
Для ряда 1го класса R=0, а для ряда 2го класса R=∞.
Поиск радиуса:
пусть имеется степ.ряд
и пусть сущ-ет конечный предел
 |=L
, тогда R=
|=L
, тогда R= .
.
Если L=∞,
то R=0
и если L=0,
то R=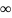 .
.
№35. Система линейных уравнений
Системой линейных уравнений с n неизвестными называется система вида (1)
 +…+
+…+ =
=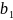
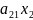 +
+ +…+
+…+
 =
=
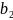
…………………………………………
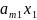 +
+
 +…+
+…+
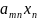 =
=
 – коэффициенты
при переменных
– коэффициенты
при переменных
Х - переменные
 =1,…,m
=1,…,m
 1,…,n
1,…,n
 (i
– 1,…,m)
- свободн.члены.
(i
– 1,…,m)
- свободн.члены.
Решением системы
(1) назыв-ся совок-ть, состоящая из n
чисел (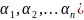 при подстановке которой вместо
при подстановке которой вместо
 ,
,
 ,…
,…
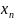 соответственно
в систему (1) каждое ур-ие этой системы
обращается в верное равенство.
соответственно
в систему (1) каждое ур-ие этой системы
обращается в верное равенство.
Система, не имеющая решений, наз-ся несовместной, система имеющая решения наз-ся совместной. Если совместная система имеет единственное решение, то её наз-ют определенной, если же она имеет больше 1 решения, то неопределенной.
№36. Решение с помощью обратной матрицы
Пусть имеется система линейных уравнений, у которой число уравнений совпадает с числом переменных (m=n)
+…+ =
+ +…+ =
…………………………………………
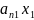 +
+
 +…+
+…+
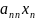 =
=
Пусть определитель матрицы системы . Это означает что для матрицы А существует обратная матрица.
В матричной форме записи этой системы (АХ=В) обе части равенства слева умножим на А-1.
А-1*A*X= А-1*B
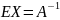 *B
*B
Х= А-1*В
Пример:
2
+
-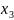 =8
=8
- +2 = -1
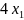 -2
+3
=1
-2
+3
=1
А= 2 1 -1
1 -1 2
4 -2 3
В= 8
-1 - столбец свободных членов
1
Найдем обратную матрицу по отношению к А.
|А|=-6 + 2 + 8 - 4 + 8 -3= 5
А’= 2 1 4
1 -1 -2
-1 2 3
 =
= (-3+4)=1
(-3+4)=1
 =
= (3-2)=-1*1=1
И т.д.с остальными.
(3-2)=-1*1=1
И т.д.с остальными.
А˜= 1 -1 1
5 10 -5
2 8 -3
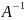 =
=
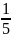 *
1 -1 1
*
1 -1 1
5 10 -5
2 8 -3
Х= * 1 -1 1 8 10 2
5 10 -5 * -1 = * 25 = 5
2 8 -3 1 5 1
ОТВЕТ: =2, =5, =1.
