25.Виток с током в магнитном поле.

Р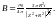 ассмотрим такой элементарный круговой виток. Воспользуемся полученными ранее результатами для поля, созданного круговым витком с током

При условии малости

р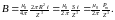 адиуса витка имеем

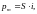
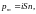
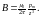
П 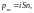оведение элементарного витка с током удобно описывать с помощью магнитного момента

где n - нормаль к контуру, направление которой связано с обходом по контуру правилом правого винта.

Магнитный момент витка с током аналогиченгиченсобственному моменту диполя.

Рассмотрим поведение витка с током в магнитном поле.

С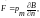 ила, действующая на виток с током в магнитном поле равна

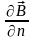
Г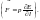 депроизводная вектораBпо

н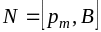 аправлению нормали. Сравним с диполем

Расчет дает -

д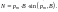 ля контура с током в однородном магнитном поле и для элементарного контура с током. Модуль момента сил равен

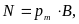
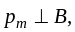
Если, то N=0,если то

е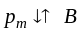 сли , то N=0, но положение равновесия неустойчивое. Мал малейшее отклонение от этого положения приводит к появлению момента сил, стремящегося отклонить контур от этого положения еще больше.

26.Линии вектора магнитной индукции. Теорема Гаусса для вектора в.

Магнитное поле так же как и электрическое можно изображать графически при помощи линий индукции – это линии, касательные к которым направлены так же, как и векторB в данной точке поля. Подобно линиям напряженности электрического поля, линии магнитного поля проводят с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним было пропорционально индукции магнитного поля в данном месте. Линии индукции магнитного поля замкнуты. Поля, обладающие такими линиями, называются вихревыми.

П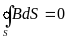 оток вектора магнитной индукции через произвольную замкнутую поверхность всегда равен нулю

Э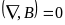 та теорема выражает тот экспериментальный факт, что магнитные линии не имеют ни начала, ни конца. В природе отсутствуют магнитные заряды на которых бы начинались и заканчивались линии вектора B.В дифференциальной форме теорема имеет вид

Магнитное поле порождают не магнитные заряды, а электрические токи.

27.Теорема о циркуляции вектора Вв интегральной и дифференциальной формах.

Ц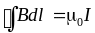 иркуляция вектора B по произвольному контуру Г равна произведениюμ0 на алгебраическую сумму токов, охватываемых контуром Г:

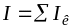
где

алгебраическая сумма токов. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта.

В ведем среднюю плотность тока, тогда

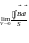
ведет себя как проекция некоторого вектора, который получил название ротора.